箱型梁極限彎矩簡化計算方法

馮亮, 董勝, 王保森, 甄春博

(1.中國海洋大學 工程學院 山東省海洋工程重點實驗室，山東青島 266100； 2.大連海事大學 交通運輸裝備與海洋工程學院，遼寧 大連 116026)

箱型梁極限彎矩簡化計算方法

馮亮, 董勝, 王保森, 甄春博

(1.中國海洋大學 工程學院 山東省海洋工程重點實驗室，山東青島 266100； 2.大連海事大學 交通運輸裝備與海洋工程學院，遼寧 大連 116026)

本文采用有限元法與強度穩定綜合理論(combined theory of strength and stability，CTSS)公式研究箱型梁的極限強度問題。揭示了有限元計算方法的不穩定性，結合Vasta的始屈彎矩法提出箱型梁結構的極限彎矩簡化計算公式。通過兩個箱型梁結構的實例計算表明，該公式的計算結果相對于試驗結果的誤差在10%以內，且與非線性有限元法相比有著簡單、穩定的優勢，可以為工程設計提供參考。

強度穩定綜合理論；加筋板；箱型梁；極限強度；初始缺陷；有限元

船體結構是典型的加筋板組合的變截面箱型梁結構，它的極限彎矩是標志其承載性能的重要指標，一直以來都受到人們的廣泛重視。目前對船體結構總縱強度的計算普遍采用三種計算方法：直接計算法、逐步破壞法以及非線性有限元法，并且這三種方法都融入到最新的共同規范計算中。直接計算法通過計算箱型梁受壓折減后剖面模數的改變來計算箱型梁的極限彎矩，計算顯示這樣的失效方式會存在一定的誤差，有時計算結果會偏于危險且不能考慮結構缺陷所帶來的影響[1-2]；逐步破壞法是通過計算船體梁曲率與彎矩的關系來選取極限彎矩，其算法的計算結果取決于單元應力應變的準確性[3]；而非線性有限元法，由于其使用的復雜性，一般的設計人員很難準確掌握邊界條件、網格密度、初始缺陷等參數取值，致使結果會顯現了很大的不穩定性[4-7]。

本文將強度穩定綜合理論(combined theory of strength and stability，CTSS)與Vasta的始屈彎矩公式相結合，得出箱型梁結構的極限彎矩公式，并與試驗結果和非線性有限元法計算結果相比較。

1 金屬材料切線模量簡化計算公式

為了考慮材料物理非線性的影響,推導出更加準確的結構極限強度簡化計算公式, 研究多種金屬材料的共性表達式是必要的。

文獻[8-9]中認為大量船用鋼材的切線模量因子曲線的非線性段可采用式(1)作為近似的數學擬合，并且認為鋼材統一采用式(2)的曲線擬合是偏于保守的：

ψ=1-gΦt

(1)

σ=1-0.25Φt

(2)

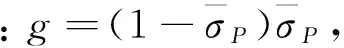
文獻[10]對15種材料進行了分析得出，式(3)可以作為很多材料非線性段的基本曲線：

σ=1/(1+0.25Φt)

(3)

2 結構極限強度的求解方法

強度穩定綜合理論(CTSS)是以強度利用率函數即切線模量因子曲線方程來對結構極限強度問題進行求解的。通常對于一般的材料均可以用下式四參數方程統一：

(4)

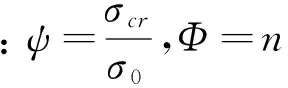
1)當φ>1時，結構處于線性階段，其強度與穩定綜合破壞的綜合因子n為

2)當φ≤1時梁柱穩定破壞的綜合因子n通常采用經驗公式或者經驗數值來進行選取，有一定的經驗成分。由文獻[8-9，11]可知，對于含通常初始缺陷的船用板結構可取綜合因子n=1.15。

對于Q235和HT32的鋼結構，非線性段也可采用切線模量因子的簡化公式(1)，此時式(4)可簡化為

(5)

其中，gQ235=0.16,gHT32=0.25。

式(5)中線性段僅適用于梁柱結構，對于板格結構由于存在后屈曲問題，其歐拉解小于其極限強度最終值，需要通過經驗公式或者屈曲系數χ的修正來得到準確值，同時Φp的大小也因此呈現出一定的不穩定性，需要具體討論。表1總結了結構失效模式中強度失效與穩定失效的耦合方式[11-13]。

表1 強度穩定綜合失效極限平衡狀態

Table 1 Ultimate equilibrium state of strength and stability

極限平衡狀態穩定理論第二類穩定問題壓彎強度理論彎曲強度理論軸向壓力N=NEN1n>1n=∞

3 加筋板結構的極限強度分析

加筋板的幾何結構與承壓性能均優于板和梁，因此在船舶與海洋工程結構中被廣泛應用。通常認為加筋板有六種失效模式，相應的結構系數計算公式如下：

1)加強筋間板的失效

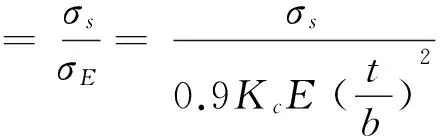
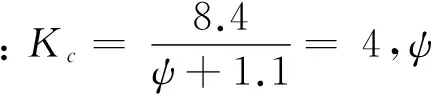
2)加強筋的腹板局部失效

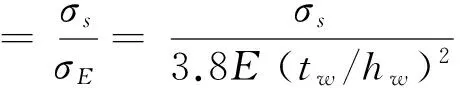
3)加筋板結構的整體失效

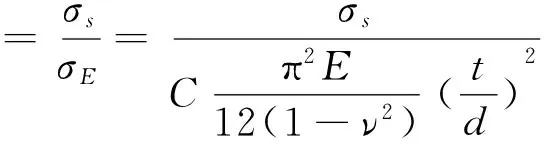
4)加筋板的梁柱失效

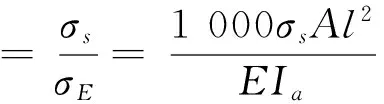
5)加強筋的側傾失效

結構系數[14]：

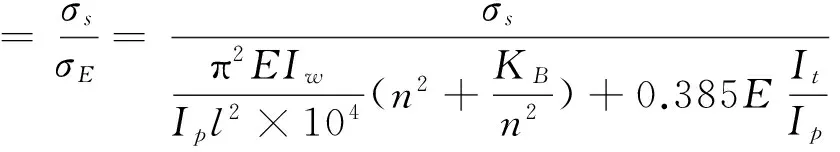
6)加強筋的面板局部失效

通常船舶加筋板的面板的寬度(對于T型材為面板的半寬)與面板厚度的比小于15，此時該種失效模式可以忽略。

當加筋板發生加強筋間板的失效后，不會立即破壞，而是將壓力進行重新分配到加強筋上，這樣加強筋的壓力將會增加，直到發生其他三類的失效模式，所以對加筋板的極限強度計算應該充分考慮這種失效模式之間的轉換而最后形成的破壞應力。

文獻[15]利用以上CTSS計算公式詳細分析了七種典型船舶與海洋工程結構加筋板的極限強度，得出該公式計算結果相對保守、穩定，可以為工程設計提供參考。

4 箱型梁的極限彎矩計算

始屈彎矩法認為船體甲板或底板受壓板架的破壞是引起船體梁破壞的主要原因，于是得船體梁的極限彎矩為

Mu=σuW

式中：σu為受壓板架的極限強度，W為甲板頂端或者底板底端的剖面模數。

下面將采用強度穩定綜合理論(CTSS)與始屈彎矩相結合的公式得出Nishihara箱型梁和Recklin23箱型梁結構的極限彎矩來分析該方法結果的可信度。

兩個箱形梁模型含有一定的初始缺陷和殘余應力,其結構形式如圖1所示，結構參數如表2所示,剖面模數如表3所示。

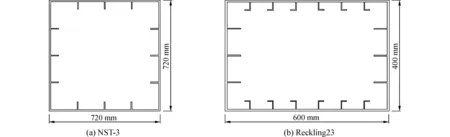
圖1 箱型梁模型橫剖面結構Fig.1 Cross section of box girder beams

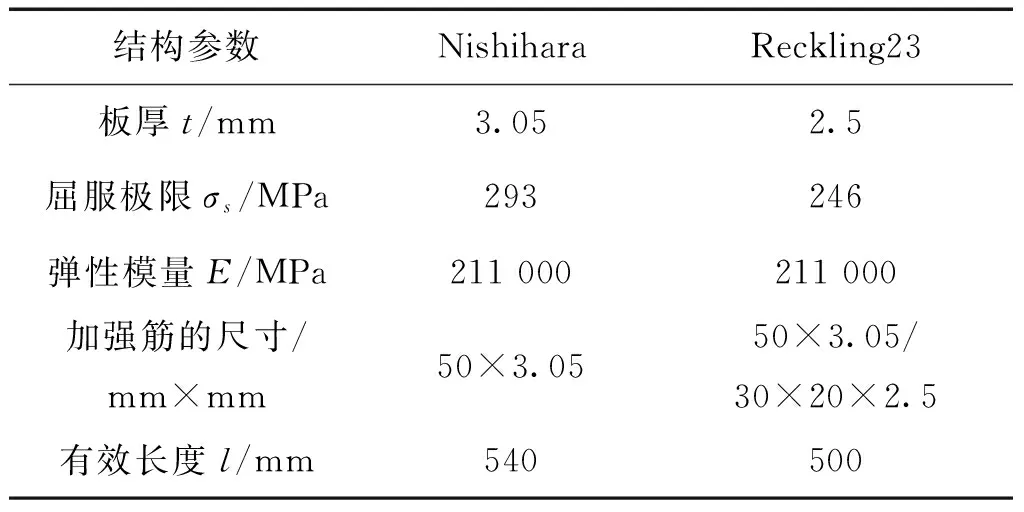
結構參數NishiharaReckling23板厚t/mm3.052.5屈服極限σs/MPa293246彈性模量E/MPa211000211000加強筋的尺寸/mm×mm50×3.0550×3.05/30×20×2.5有效長度l/mm540500

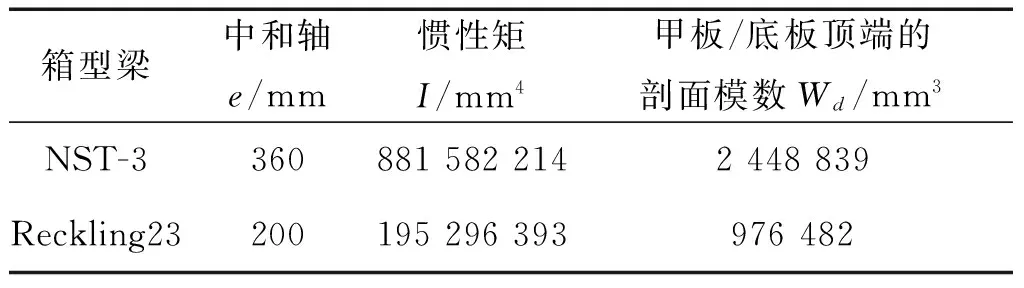
表3 箱型梁模型的剖面模數

表4為采用CTSS方法與有限元方法得到的箱型梁甲板(或底板)的極限強度數值，其中CTSS方法中材料切線模量公式采用下式：

(6)

失效模式為加強筋間板的失效，表5為箱型梁甲板(或底板)5種失效模式計算結果及其最終結果。有限元方法中材料的本構關系采用理想應力應變關系，圖2為有限元法甲板失效時的圖片。

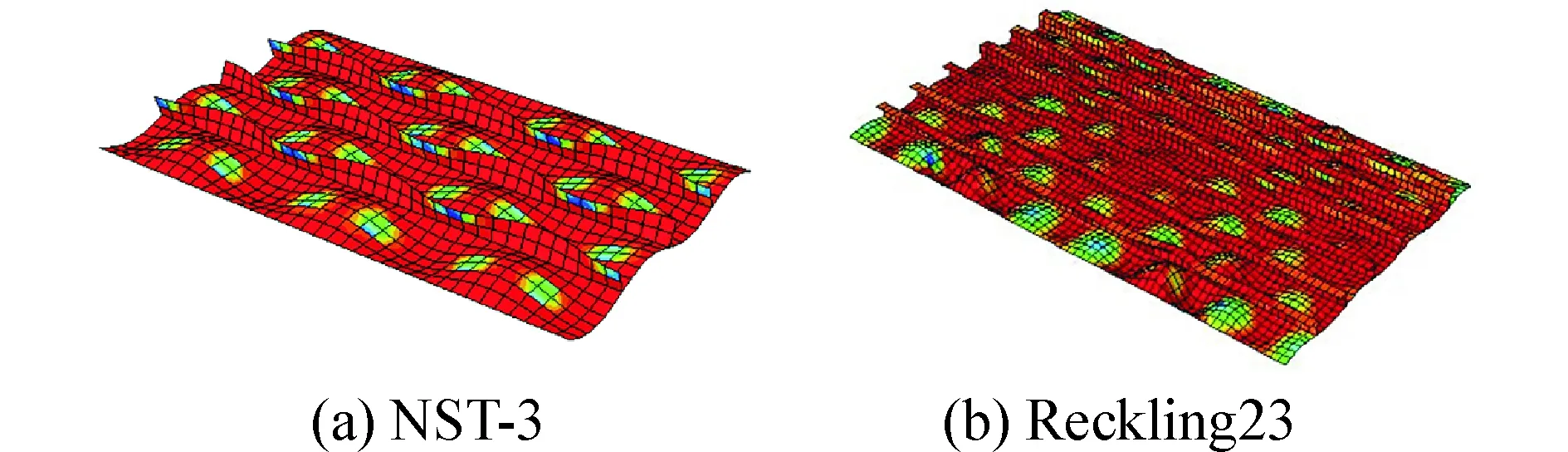
圖2 箱型梁甲板極限狀態Fig. 2 Ultimate state of deck of box girder beam

Table 4 Calculation result of deck(or bottom) under four failure modes MPa

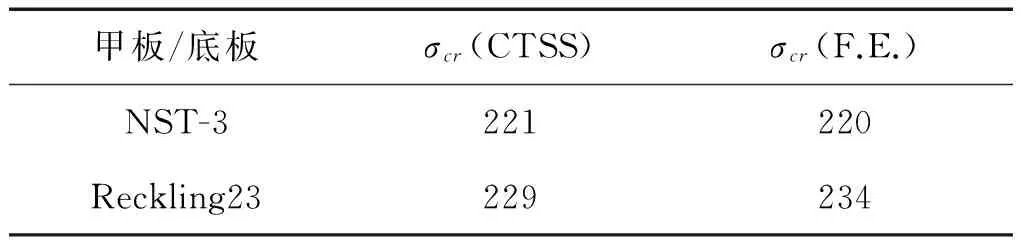
甲板/底板σcr(CTSS)σcr(F.E.)NST-3221220Reckling23229234

表5 五種失效模式計算相對結果

Table 5 Calculation ratio results of five kinds of failure modes by CTSS

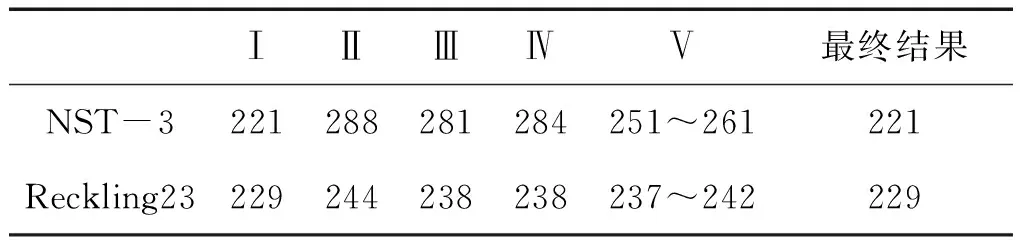
ⅠⅡⅢⅣⅤ最終結果NST-3221288281284251～261221Reckling23229244238238237～242229

表6為兩個箱形梁的試驗值、有限元法與本文的計算結果比對，從中可以看出，有限元法雖然有一定的精度，但存在一定的不穩定性，主要取決于網格大小、初始缺陷選取位置、選取的模態和比例因子數值。

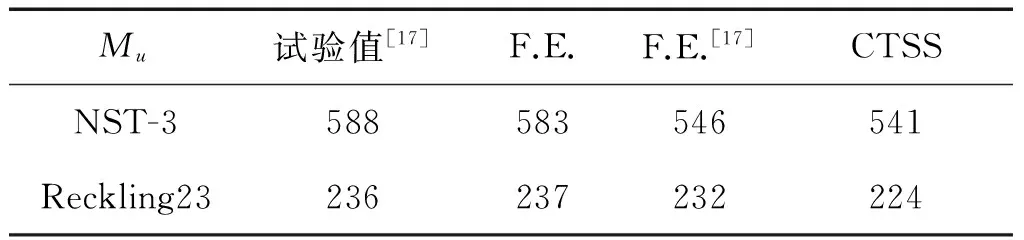
表6 NST-3模型計算結果及比較

表7揭示了兩個箱型梁初始缺陷中不同比例因子對有限元計算結果的影響。結果顯示由于比例因子數值選取的不同，結果偏差通常會達到4%左右。

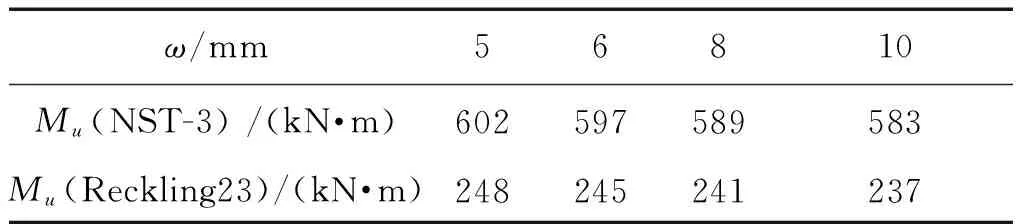
表7 四種不同比例因子數值計算結果

表8揭示了兩個箱型梁網格的不同劃分對有限元計算結果的影響。結果顯示由于網格大小選取的不同，結果偏差甚至會達到30%多。

表8 四種網格模型數值計算結果

Table 8 Four kinds of numerical results of mesh models

網格尺寸/mm2550100150Mu(NST-3)/(kN·m)580586776800Mu(Reckling23)/(kN·m)225247259273

圖3是有限元法得出的兩個箱型梁理想時的極限狀態，從中可以看出，NST-3箱型梁是由于加強筋間板的破壞而最終破壞的，這與采用CTSS法所計算的失效模式一致。Recklin23箱型梁是由于加強筋間板的破壞且伴隨著整體失穩而最終破壞的，這同樣與采用CTSS法所計算的失效模式一致。

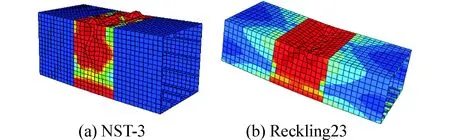
圖3 箱型梁理想模型極限狀態Fig. 3 Ultimate state of box girder beams

綜合以上結果可得：本文提出的CTSS法雖然沒有考慮箱型梁整個破壞過程，但與試驗值和非線性有限元法相比具有著簡單、穩定的優勢，可以為工程設計提供參考。

5 結論

1) 本文將CTSS公式與始屈彎矩相結合得出箱型梁結構的極限彎矩計算公式，通過對兩個箱型梁的實例分析，得出該種計算方法的計算結果相對于試驗結果的誤差在10%以內，且與非線性有限元法相比有著簡單、穩定的優勢，有一定工程參考價值。

2) 船體結構是復雜的箱型梁結構，本文所提出的計算方法雖然得到了兩個簡單箱型梁的驗證，但仍需得到實際工程的檢驗，所以需要繼續探索。

[1]CALDWELL J B. Ultimate longitudinal strength[J]. Transactions of RINA, 1965, 107: 411-430.

[2]FAULKNER D. A review of effective plating to be used in the analysis of stiffened plating in bending and compression[J]. Journal of ship research, 1975, 19(1): 1-17.

[3]SMITH C S. Influence of local compressive failure on ultimate longitudinal strength of a ship’s hull[C]//PRADS-International Symposium on Practical Design in Shipbuilding. Tokyo, 1977: 73-79.

[4]PAIK J K, KIM B J, SEO J K. Methods for ultimate limit state assessment of ships and ship-shaped offshore structures: part III hull girders[J]. Ocean engineering, 2008, 35(2): 281-286.

[5]PAIK J K, KIM D K, PARK D H, et al. Modified Paik-Mansour formula for ultimate strength calculations of ship hulls[J]. Ships and offshore structures, 2013, 8(3/4): 245-260.

[6]KIM D K, PEDERSEN P T, PAIK J K, et al. Safety guidelines of ultimate hull girder strength for grounded container ships[J]. Safety science, 2013, 59: 46-54.

[7]GARBATOV Y, SAAD-ELDEEN S, SOARES C G. Hull

girder ultimate strength assessment based on experimental results and the dimensional theory[J]. Engineering structures, 2015, 100: 742-750.

[8]馮亮, 佟福山. 基于簡易切線模量法的中厚度板殼極限強度分析[J]. 武漢理工大學學報, 2012, 34(4): 57-61. FENG Liang, TONG Fushan. Ultimate strength research of plates and shells based on simple tangent modulus factor method[J]. Journal of Wuhan university of technology, 2012, 34(4): 57-61.

[9]馮亮, 佟福山. 基于強度穩定綜合理論的加筋板極限強度分析[J]. 哈爾濱工程大學學報, 2011, 32(12): 1539-1543. FENG Liang, TONG Fushan. Ultimate strength research of stiffened panels based on the combined theory of strength and stability method[J]. Journal of Harbin Engineering University, 2011, 32(12): 1539-1543.

[10]熊志鑫, 羅培林. 承壓結構極限載荷的切線模量因子法表達研究[J]. 華中科技大學學報: 自然科學版, 2013, 41(4): 109-113. XIONG Zhixin, LUO Peilin. Expressing limit loads of pressurized structures by tangent modulus factors[J]. Journal of Huazhong university of science and technology: natural science edition, 2013, 41(4): 109-113.

[11]馮亮, 佟福山. 梁柱復雜穩定性的非線性研究及其擴展[J]. 華中科技大學學報: 自然科學版, 2012, 40(9): 114-117. FENG Liang, TONG Fushan. Geometric nonlinear complex stability research for beam-to-column and it′s extension[J]. Journal of Huazhong university of science and technology: natural science edition, 2012, 40(9): 114-117.

[12]馮亮. 基于強度穩定綜合理論的船體結構極限強度研究[D]. 哈爾濱: 哈爾濱工程大學, 2012. FENG Liang. Ultimate strength research of ship structure based on combined theory of strength and stability[D]. Harbin: Harbin Engineering University, 2012.

[13]羅培林. Hooke′s Law(胡克定律)的革新與“強度穩定綜合理論”的創建和發展[J]. 哈爾濱工程大學學報, 2008, 29(7): 641-650. LUO Peilin. The establishment and development of a combined theory of strength and stability based on innovative Hooke′s law[J]. Journal of Harbin engineering university, 2008, 29(7): 641-650.

[14]中國船級社. 鋼質海船入籍規范[M]. 北京: 人民交通出版社, 2009: 59-61.

[15]馮亮, 董勝, 王保森, 等. 加筋板極限強度簡化計算及其可靠性分析[J]. 華中科技大學學報: 自然科學版, 2016, 44(9): 71-76. FENG Liang, DONG Sheng, WANG Baosen, et al. Simple method for ultimate strength calculation and reliability analysis of stiffened plates[J]. Journal of Huazhong university of science and technology: natural science edition, 2016, 44(9): 71-76.

[16]ESTEFEN T P, ESTEFEN S F. Buckling propagation failure in semi-submersible platform columns[J]. Marine structures, 2012, 28(1): 2-24.

[17]白寶強. 船體梁極限強度的非線性有限元分析[D]. 哈爾濱: 哈爾濱工程大學, 2009. BAI Baoqiang. The ultimate strength analysis of the ship hull girder based on NFEM[D]. Harbin: Harbin Engineering University, 2009.

Simplified method for calculating ultimate bending moment of box girder

FENG Liang1, DONG Sheng1, WANG Baosen1, ZHEN Chunbo2

(1. Shandong Provincial Key Laboratory of Ocean Engineering, College of Engineering, Ocean University of China, Qingdao 266100, China; 2. Transportation Equipment and Ocean Engineering College, Dalian Maritime University, Dalian 116026, China)

In this study, we used the finite element method and the combined theory of strength and stability (CTSS) to determine the ultimate strength of the box girder. Due to the instability of the finite element method alone, we propose a calculation formula that simplifies the ultimate bending moment of the box girder by its combination with the initial-flexion bending moment method defined by Vasta. In two calculation cases of the box girder structure, our test results show that the calculation errors associated with this formula are less than 10%. In addition, in comparison with the nonlinear finite element method, our proposed method is simple and stable, and can provide a reference for engineering design.

combined theory of strength and stability; stiffened plates; box girder; ultimate strength; initial imperfection; finite element method

2015-11-10.

日期：2017-01-11.

國家自然科學基金項目(51479183，51309209)；上海交通大學海洋工程國家重點實驗室研究基金項目(1404)； 中國海洋大學山東省海洋工程重點實驗室研究基金項目(201462010)；青年教師科研專項基金項目(201513042).

馮亮(1983-)，男，博士，講師； 董勝(1968-)， 男，教授，博士生導師.

董勝， E-mail: dongsh@ouc.edu.cn.

10.11990/jheu.201511017

U661.43

A

1006-7043(2017)03-0351-05

馮亮, 董勝, 王保森，等.箱型梁極限彎矩簡化計算方法[J]. 哈爾濱工程大學學報, 2017, 38(3):351-355.

FENG Liang, DONG Sheng, WANG Baosen，et al.Simplified method for calculating ultimate bending moment of box girder[J]. Journal of Harbin Engineering University, 2017, 38(3):351-355.

網絡出版地址：http://www.cnki.net/kcms/detail/23.1390.u.20170111.1509.004.html