新高考背景下高中非畢業年級數學命題策略研究

趙爽

[摘 要] 筆者任教于重慶市南開中學高中部，關注到校內甚至全市對“適應全國卷新高考”的教學和復習備考策略的研究氛圍濃厚，但對非畢業年級的關注和研究較少，尤其是對非畢業年級同步教學命題工作的應對策略研究很少. 本文將通過全國卷數學學科在試題結構、考點分布、考題難度等方面的特點，對比并總結出相關變化，提出非畢業年級在同步教學命題工作中的應對策略，以期對正在高一、高二年級任教的數學教師在同步教學命題和適應全國卷的教學上提供些許幫助.

[關鍵詞] 新高考；全國卷；非畢業年級；命題特點；應對策略

[?] 研究背景

2014年9月4日，國務院頒布了《關于深化考試招生制度改革的實施意見》，明確指出，深化高考考試內容的改革，2015年起增加使用全國統一命題試卷的省份. 從2016年開始，重慶高考采用全國卷已毫無懸念，而全國卷和重慶卷不管是在試卷結構方面還是在從考試范圍與內容方面，考試的主干內容側重點與位置擺放方面以及更深入一點的試卷梯度、區分度方面都有著明顯的不同. 在這種背景下，研究新形勢下高中數學教學和命題的應對策略就顯得很有必要了.

現在大多數關于新高考全國卷命題和備考復習工作的研究，都是針對畢業年級的，對非畢業年級的教學、備考、命題研究卻為數不多. 從長遠來看，適應全國卷命題的工作應該盡早開展，在高一、高二的教學、命題、評價等教學環節中都應盡早地適應全國卷的評價標準，使教師的教學工作更有的放矢，使學生的學習過程更有益于能力的提高.

[?] 新高考數學全國卷的命題特點簡析

1. 結構變化，立足基礎，考查全面

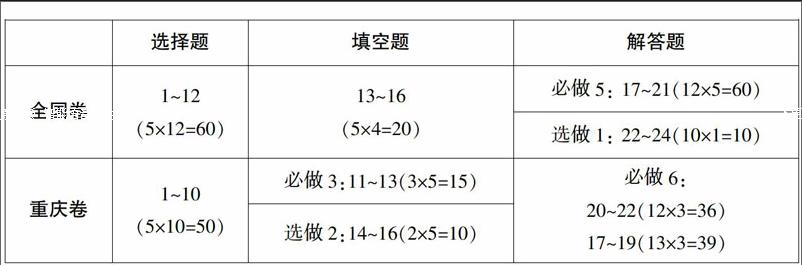
首先是各題型試題數目和分值的變化，值得關注的是對選修內容的考核. 由重慶卷填空題三選二，變為全國卷的解答題三選一，由題型變化和題數變化帶來了難度的變化. 整體來看，全國卷對選修內容的考核難度較之重慶卷有所提升，但基礎知識的比重仍是最大，且基礎知識中尤其重視通式通法的考查. 相比于重慶卷，全國卷中等難度問題會更多一些，難題和簡單題都會少一些，讓更多的學生能做到所有試題，更全面地考查學生的知識和能力.

2. 內容變化，突出主干、重視通法，注重思維能力的考核

相較重慶卷，全國卷有一些“新增”內容：三角恒等變換中積化和差、和差化積、半角公式等，曲線與方程，統計案例中的獨立性檢驗、正態分布、線性回歸方程，定積分與微積分基本定理，選修系列4不等式的證明等，這些都是重慶卷不考的內容或者邊緣的內容，但卻已經多次出現在新課標全國卷的內容中. 此外，筆者還關注到，統計學的獨立性檢驗、線性回歸方程、正太分布越來越多地出現在全國卷的考題中，多以實際問題為背景. 如2015年新課標Ⅱ卷第18題考查了莖葉圖和獨立性檢驗，2014年新課標Ⅱ卷和2015年新課標Ⅰ卷第19題均考查了線性回歸方程，2014年新課標Ⅰ卷第18題考查了正態分布. 數學應用越來越受到命題組的青睞.

另外，解答題部分，全國卷在題目考核知識點上也具有一定的穩定性，通過對比能夠看出，變化主要體現在數列、函數與導數、選修內容的考法上. 其中全國卷數列問題主要考查數列的性質、通項與前n項和，通常位于第一個解答題，難度較低；而重慶卷主要考查數列不等式，通常位于壓軸題的位置，對學生的綜合能力要求頗高，難度大不易得分. 全國卷的壓軸題多以函數導數內容為主，主要涉及恒成立、參數問題、最值問題和不等式問題，題目條件簡潔常規，雖有難度但相對較易入手；而重慶現行高考中通常將函數導數問題設置為中等難度的解答題，不作為壓軸題出現.

3. 穩中求新，思辨性強，重視遷移能力的考查

全國卷立足課標，考點相對穩定，但載體時常革新，經常在高中數學知識模塊交匯處，在中學數學與高等數學交匯處設計問題，以競賽數學思想或改編競賽題的情境命制高考題目，考查教材中出現過的高等數學思想、數學文化，用創新形式的方式實現遷移能力的考查. 而在競賽背景下和高等數學背景下設計的題目往往具有極強的思辨性，需要學生在數學思想的高度尋求解題突破口，充分考查學生的數學學習能力和問題解決能力.

例：（2013年新課標Ⅰ卷12題）設△AnBnCn的三邊長分別為an，bn，cn，△AnBnCn的面積為Sn，n∈N*，若b1>c1，b1+c1=2a1，an+1=an，bn+1=，cn+1=，則（ ）

A. {Sn}為遞減數列

B. {Sn}為遞增數列

C. {S2n-1}為遞增數列，{S2n}為遞減數列

D. {S2n-1}為遞減數列，{S2n}為遞增數列

答案：B. 本題在數列知識和解析幾何知識交匯處設題，體現由數到形的轉化、抽象到具象的轉化，著重考查數形結合、極限、轉化與化歸等數學思想方法以及分析問題、解決問題的能力和創新能力，是該套高考試卷的一個亮點.

[?] 非畢業年級試題命制的應對策略

非畢業年級的教學工作要立足新高考對學生知識和能力的要求，在教學過程中貫徹落實教材中滲透的基礎知識技能、數學思想方法、數學思維能力、數學文化素養，并在命題中充分設計考點考題，最大限度地擬合高考命題的特點，達到多方位立體檢測知識和能力的目的.

1. 結構對接，基礎知識和基本技能重點考查

首先，試題的結構是決定學生考試時間分配的關鍵，所以在同步教學試題命制時，教師應有意識地按照高考試卷的結構命題，即按照12道選擇題、4道填空題、6道解答題的題量、題型設定，以保證學生適應跟高考相似的考試模式. 另外，同高考命題指導思想一致，同步章節的命題也要重視對階段內基礎知識、基本技能、基本思想方法的考查，在主觀題、客觀題上始終按照先易后難的順序進行排列，便于學生在考試時能順利地進入狀態并穩定發揮. 值得關注的是，高考全國卷最后的第22題、第23題、第24題均是分值為10分的選做題，學生需擇其一而答，內容為選修新增的內容，考核難度較低. 那么，在學生學習這些知識前，非畢業年級無法直接以三選一的形式仿真考查，這時我們可以模擬高考中該類問題的難度，設計一道較為基礎的解答題（筆者所在學校即把第17題設定成為10分的題目），用以考查階段內最基礎的主干內容.

近年來，高考試卷中基礎題、中檔題、難題的分值比例基本穩定在6∶3∶1，因此，對非畢業年級試題的命制也要按這一比例分配各梯度層次的題目. 在基礎知識和基本技能的考核題目中，要依據高考的標準，注重通式通法，淡化特殊技巧，回避重復、繁雜的機械運算.

2. 選題有道，適應全國卷能力立意的指導思想

遵循命題的公平性原則，一次重要的考試，不該使用成卷或成題，因此要求命題者改編或原創出符合命題要求的各類型試題.

（1）立足基礎，回歸教材，提高試題輻射廣度，嚴控試卷絕對難度.

試卷中避免成題是為了確保試題的公平性，但教材中的例題和課后配備的習題和拓展資料對每個考生而言都是公平的. 筆者在實際教學過程中發現，很多學生對數學教材的重視度不夠，部分教師對教材滲透的潛在知識和思想挖掘不深，導致教材未能發揮最大作用. 然而，縱觀近3年全國卷的高考試題，總會發現取材課本的案例. 因此，筆者認為，適應新高考，首要的任務是適應新高考“立足基礎，回歸教材”的指導思想. 選編課本原題，仿制課本例題，生成課本變題，一方面能保證大部分考生獲得基本分數，另一方面也能引導師生吃透教材、深研教材. 但改編教材題目作為考試題目要注意：題目要具有典型性，同套試卷中數量不宜過多，以免導致學生“死記硬背”的應對策略. 選用教材題目或素材，是為了讓學生在熟悉的題境中解決問題，但不代表這類題目是蒼白的送分題，可以通過合適的設計讓學生感受到題目的“數學味”，常用的方法有：改變題型、數據、圖形、情境、背景，對已有結論進行推廣延伸，跨章節素材整合等.

原題：（人教版必修1第83頁B組第4題）設f（x）=，g（x）=.

求證：（1）[g（x）]2-[f（x）]2=1；

（2）f（2x）=2f（x）·g（x）；

（3）g（2x）=[g（x）]2+[f（x）]2.

改編1：設f（x）=，g（x）=，給出如下結論：

①對任意x∈R，有[g（x）]2-[f（x）]2=1；②存在實數x0，使得f（2x0）>2f（x0）·g（x0）；③不存在實數x0，使g（2x0）<[g（x0）]2+[f（x0）]2；④對任意x∈R，有f（-x）g（-x）+f（x）g（x）=0.

其中所有正確結論的序號是________. （答案：①③④）

改編2：已知函數F（x）=ex滿足F（x）=g（x）+h（x），且g（x），h（x）分別是R上的偶函數和奇函數，若?x∈[1，2]，有不等式g（2x）-ah（x）≥0恒成立，則實數a的取值范圍是________. （答案：a≤2）

改編3：已知定義在R上的奇函數f（x）和偶函數g（x）滿足f（x）+g（x）=ex，則=______________ . （答案：）

（2）創新情境，適度綜合，注重數學思想和數學文化的考查.

適應全國卷的高考數學命題，尤其要適應以一定程度的綜合性、創新性為表征的數學思想和數學文化的考查要求，這二者著重考查學生的問題解決能力、數學抽象能力等數學學習能力，難以一蹴而就，最好讓非畢業年級就開始適應這樣的題目和考法.

這就要求非畢業年級的命題者在選題、編題、創題的過程中更注重設計題目的潛在考點和深層立意，用高考常用的命題方法指導同步教學的命題，如在知識交匯處命題，以數學史料、數學文化為背景命題，在實際背景下編制數學應用問題，甚至將高考真題和模擬題進行改編或仿真原創，充分體現考查數學思想、數學文化的命題原則.

但對于非畢業年級的命題而言，編制此類試題的綜合度不宜過高，數量不宜過多，以當下學習時段內的知識為主干，適當地進行知識遷移或拔高拓展即可. 適合編制部分中等難度的主、客觀題目和較難的壓軸題目，中檔題要讓多數學生有發揮和探究的空間和時間，壓軸題目也要通過題設條件和背景的設計，給學生以適度提示. 像全國卷的壓軸題一樣，起點很高但落點很低，讓能力稍差的學生因不陌生而產生勇氣，讓能力強的學生因深入探究而感受到隱藏的價值和深意.

如下幾道題目，均是高一年級所學知識，在數列和平面向量三點共線知識的交匯處設題，隨著題設條件的改變，綜合度和難度截然不同. 試題1考查等差數列的性質、等差數列的前n項和公式和三點共線系數和為1，比較容易，適合設置在第7或第8題；試題2考查數列遞推公式求通項、等比數列前n項和公式、分組求和法、三點共線系數和為1，適合設置在第14或第15題；試題3考查數列遞推、周期數列、并項求和法、三點共線系數和為1，其中周期的推導和發現較難，適合設置在第15或第16題；試題4考查數列遞推、裂項求和、數列單調性、三點共線系數和為1，其中對遞推公式進行裂項是難點，適合設置在第16題.

試題1：已知{an}為等差數列，Sn為數列{an}的前n項和，平面內三個不共線的向量，，，滿足=（a17-2）+a2000，若點A，B，C在同一條直線上，則S2016=（ ）（答案：A）

A. 3024 B. 2016

C. 1008 D. 504

試題2：Sn為數列{an}的前n項和，a1=1，平面內三個不共線向量，，，滿足=an+1-2an（n∈N*），若點A，B，C在一條直線上，則Sn=_________.（答案：2n+1-n-2）

試題3：Sn為數列{an}的前n項和，a1=a2=1，平面內三個不共線向量，，，滿足=（an+1+an-1）+（1-an）（n≥2，n∈N*），若點A，B，C在一條直線上，則S2018=________.（答案：2）

試題4：數列{an}與平面內三個不共線向量，，滿足=-an，a1=1，Sn為數列

的前n項和，用[x]表示不超過x的最大整數，則當三點A，B，C 在一條直線上時，[S2016]=（ ） （答案：A）

A. 0 B. 1 C. 2 D. 3

（3）高觀點立題，能力立意，在高等數學背景下設題.

針對高考中頻繁出現的基于競賽和高等數學背景的題目，這些題目往往難度較大或形式新穎，對學生綜合能力的要求高，需要從起始年級開始接觸和適應這種立足高觀點的試題. 事實上，高中的很多概念都是高等數學知識的下放，命題者可以在這些概念上做文章命制題目，也可以借助高等數學或數學史中的著名問題命制題目，甚至可以嘗試編制一些能用高等數學中的初等方法來解決的問題作為考試題目.

但這一命題方法要求命題者具有較高的專業素養和改編能力，把起點很高的高等數學中的抽象問題具象化，改編成高中學生認知能力范圍內的題目，需要命題者在教學過程中，不斷積累素材并及時進行教學研究，多嘗試，多打磨，才有可能命制出一道高質量的高中數學題目.

以下幾例均為函數和導數模塊中，在高中常見的有高等數學背景的題目. 其中，試題5以考查函數的一階不動點為背景，將其具象化后編制的題目，適合高一學生學完函數后作為檢測；試題6和試題7實際上是以高等數學中拉格朗日中值定理為理論依據而命制的題目，學生如果知曉該定理的簡單含義或是幾何意義，可轉化為導函數取值范圍問題或通過高中“構造函數”的思想進行解答，適合高二學習導數后作為試題檢測；試題8（2）可以用高中函數和導數知識及換元思想完成解答，但實際上若能化歸成近年高考中高頻考點“極值點偏移”問題，更易找到巧妙解法，而“極值點偏移”的背景是高等數學中連續函數凹凸性的問題，該題對學生的能力要求較高，可在高二學過導數后作為考試的壓軸題目.

試題5：已知函數y=f（x）在定義域（0，+∞）上是單調函數，若對任意x∈（0，+∞），都有ff（x）

-=2，則f

的值是________.

試題6：已知函數f（x）=-x3+ax2+b，若y=f（x）圖像上任意不同兩點連線的斜率都不大于1，則a的取值范圍是______.

試題7：已知函數f（x）=x2-2x，g（x）=logax（a>0，a≠1）. 如果h（x）=f（x）+g（x）是增函數，且h′（x）存在零點（h′（x）為h（x）的導函數）.

（1）求a的值；

（2）設A（x1，y1），B（x2，y2）（x1

試題8：已知函數f（x）=lnx-ax，a為常數，a∈R.

（1）討論函數f（x）在定義域上的單調性；

（2）若函數f（x）有兩個零點x1，x2，證明：x1x2>e2.

3. 注重整體性，用科學的標準評價試題、試卷的質量和效果

每張試卷都是一個有機整體，各類型題目要合理搭配才能保證整體性. 命題過程中除了要確保做到符合學情、科學無誤、表述精準簡潔、難度適宜、導向正確外，還應該注意以全國卷的標準來把控試卷的難度系數、信度、效度和區分度. 可以用高考試題常用的公式計算上述指標，并在考前預測和考后檢測兩個環節中，檢驗試卷預期考核效果和實際考核效果的符合程度，及時進行命題工作的總結和反思，使得后續的命題工作更切合實際，更貼近高考.

高考常用的各項指標的計算過程和方法很復雜，每項指標都要用多種不同的方法進行計算，高中教師無法對每次測試的結果都進行如此細致專業的分析，但可以用簡化的方式實現上述重要指標的測試. 現提供公式如下，僅供參考：

（1）區分度μ：分數前27%的得分稱為高分組，后27%的得分稱為低分組，則μ=.

（2）信度α：σ表示第i道題目的方差，σ表示總得分的方差，k表示題目的個數，則信度系數公式為α=

（3）難度P：①客觀性試卷難度P的計算公式：P=（k為答對該題的人數，N為參加測驗的總人數）；②主觀性試卷難度P的計算公式：P=（x為試卷平均得分，M為試卷滿分）；③適用于主、客觀試卷的計算公式：P=（PH，PL分別為針對高分組和低分組的難度值）.

（4）效度：效度是指考試有效性或正確性的質量指標，即是否考了要考的內容，試題難度、區分度是否適宜，考試最終是否達到了它的預定目的. 試卷效度主要有內容效度、結構效度. 一般來說，除了要根據教學要求和有效性的理論對試卷的內容進行考察以外，還需采用計算相關系數的方法，即計算出本次試卷與另一份已被確定能正確反映受試者水平的試卷之間的相關系數來反應試卷的效度.

[?] 關于高中數學試題命制的一點思考

1. 明確試卷功能對試題命制工作的影響

目前的高中數學試卷按功能區分，大致有側重于同步檢測的診斷性試卷（如單元測試），側重于階段性知識技能考查的評價性試卷（如期中、期末考試），側重于群體區分的選拔性試卷（如高考），側重于學科人才選拔的競賽性試卷. 不同功能的試卷，在難度、目標、導向等方面均有不同的要求，同時還要因時因地制宜，符合應考學生群體的認知水平和心理承受能力. 非畢業年級主要承擔前兩種功能的試題命制，如診斷性試卷注重專題知識的深度和對知識技能應用的靈活度，目的就是查缺補漏、階段檢測，可適當地出現個別新穎別致的非常規考題，但在知識考查的廣度上，就必須有所限制；而評價性試卷是對一個學習周期內學生學習效果的綜合評定，需要涵蓋該時段內的基礎知識、基本技能、主要思維能力和數學思想方法，要具有一定的綜合度和區分度，同時也要注意難度適中，保證試題信度和效度，以達到檢測的目的.

2. 用規范的操作程序，保證試卷的整體質量

命制評價功能的數學試卷，一般要經歷四個重要的程序：

首先，要編制雙向細目表. 分析當下考試情況，結合學情，根據雙向細目表的內容、能力層次要求和課時比例，制定整套試卷的知識點分布、題型分布、能力要求、試卷布局和結構.

其次，編制各類試題形成試卷初稿. 要注意選題原則，題目的內容能代表階段知識的重點、難點，選題素材具有普適性（全國卷的命題往往基于教材，基于知識交匯點，基于高等數學背景）. 以此為指導思想，盡力擬合高考對知識和能力的要求，重視通性通法型問題的考查，重視數學思想在題目中的滲透，重視題目背后的數學文化，但務必要適合非畢業年級學生的具體情況，切忌變成高考復習題.

再次，解答全卷預測難度. 初稿形成后，命題人要先對試卷進行全面完整的作答，記錄時間，評估單題和整套試卷難度. 通常情況下，全國卷高考數學難度系數在0.6左右，競賽考試的試卷難度在0.3至0.5左右，而單元檢測、期中考試、期末考試難度不宜過大，難度系數控制在0.6至0.8左右. 事實上，難度預測本身就是很復雜的過程，主要依賴于教師的教學經驗和對全國卷數學試題難度的熟悉.

最后，試題微調訂立評分標準. 按照高考數學命題規范，調整初稿中表述不規范之處，力求條件簡潔；知識的使用過程準確無誤，改編偏、難、怪的試題形式；設計數據，讓數據處理自然、流暢；預判試題或試卷對學生能力水平的鑒別能力，使能力強的學生得高分，能力差的學生得低分，即注重試題區分度的設定，如果是重要的考試，可按照高考現行的區分度計算方法進行預測評估：一般區分度在0.4以上為優秀，0.3至0.4之間為良好，0.3以下為不合格. 最后的微調還要注意應用型問題的實際背景是否符合學生的身心特點，保證背景公平. 當題目全部調整合適后，即可按照高考的分制和分值訂立科學的評分標準.

3. 非畢業年級命題既要適應新高考又不可全然為了高考

非畢業年級命題策略調整的直接目的，是適應新高考制度下全國卷對數學思想方法、數學思維、數學應用和數學文化的考核方法，但本質目標是通過新評價標準的執行，檢測新課程理念對數學人才培養目標的實現程度，進而更好地達成目標. 所以在非畢業年級的教學和評價環節，要立足于人的全面培養和考核，因此絕對不能在起始年級就執行只教高考考綱內容、只考高考常考考點的“應試”策略. 可在學生能力范圍內，適當放寬考核范圍和考查難度，注重試題靈活性、創新性和思辨性，非畢業年級有時間和精力，適當擺脫考綱的束縛，最大程度上培養學生的數學素養，即邏輯推理、數學抽象、直觀想象、數學運算、數據分析能力，真正做到以考養學，以考養能，以考養才.