基于AIS信息的船舶航跡動態(tài)行為分析技術(shù)研究

何時浩

【摘 要】目標(biāo)船舶航跡的動態(tài)行為分析對駕駛決策、交通管制、事故分析等有著很大的意義。利用matlab編程將AIS獲取的經(jīng)緯度信息轉(zhuǎn)化成高斯平面直角坐標(biāo)系信息，對轉(zhuǎn)化后的數(shù)據(jù)運用軟件編程進行最小二乘法的三次擬合能取得較好的效果。再結(jié)合船舶操縱運動方程對擬合的曲線進行分段擬合處理，提高精度，最后通過實驗仿真進行檢驗。仿真結(jié)果表明，本文采取的算法能大大提高航跡復(fù)原的精確度，對船舶的動態(tài)行為分析起到了很大的幫助。

【關(guān)鍵詞】最小二乘法；分段擬合；航跡復(fù)原

0 引言

隨著各國海運業(yè)的發(fā)展，船舶密度的增加，船舶的安全問題就顯得特別突出，實現(xiàn)高效的交通管制和事故分析就成為各國亟待解決的問題。準(zhǔn)確地復(fù)原航跡線不僅對船舶的行駛狀態(tài)有所了解，而且對出現(xiàn)事故的船舶也能做進一步地分析處理。

首先是對AIS獲取的經(jīng)緯度位置信息進行坐標(biāo)的轉(zhuǎn)換，變成平面直角坐標(biāo)系信息，便于處理[1]；其次是先通過已知點推算臨近時刻的數(shù)據(jù)點，增加擬合點的數(shù)量，然后運用基于最小二乘法的三次擬合算法并結(jié)合船舶操縱運動方程對擬合曲線進行分段處理，提高精度[2-3]；最后是結(jié)合實例，對本算法運用matlab軟件編程進行仿真實驗，驗證其精確性。

1 數(shù)據(jù)轉(zhuǎn)換

船舶航行時，通常用的是全球定位系統(tǒng)（GPS）獲取實時信息，在研究船舶航跡過程中，常利用投影的辦法將船舶空間數(shù)據(jù)轉(zhuǎn)換為平面數(shù)據(jù)，從而可以在平面內(nèi)繪制船舶航行軌跡。本文采用的是高斯-克呂格投影將經(jīng)緯度信息轉(zhuǎn)換為平面信息[4]。

1.1 GAUSS-KRUGER變換

在高斯-克呂格投影面上，赤道與中央子午線投影后都是一條直線，我們建立坐標(biāo)系，以兩者交點O作為坐標(biāo)軸原點，縱坐標(biāo)在這里稱為x軸，對應(yīng)于中央子午線的投影直線，橫坐標(biāo)為y軸，對應(yīng)于赤道投影后的直線，這樣就形成了高斯平面直角坐標(biāo)系。

對于高斯-克呂格投影，橢球面上的一點映射到平面上的一點，計算公式用級數(shù)展開[5]；子午線弧長是橢球面上由赤道到投影點的距離，可由級數(shù)展開來計算。

1.2 數(shù)據(jù)預(yù)處理

導(dǎo)航定位的精度在數(shù)據(jù)測量方面是非常重要的。GPS本身的精度很高，但是在復(fù)雜的海況下受到氣候、溫度等因素的影響，另外還受到船身搖擺的幅度影響，這些都會影響接收機記錄數(shù)據(jù)，難以精確測定船舶的航行軌跡。在利用GPS數(shù)據(jù)計算之前，首先須對接收來的大量信息進行分離提取、顯示等環(huán)節(jié)的處理，這是保證海上地球物理調(diào)查數(shù)據(jù)質(zhì)量的前提，主要有以下幾個方面[6]：

1）獲取的數(shù)據(jù)有很多無效數(shù)據(jù)，用濾波的方法剔除；2）將數(shù)據(jù)格式統(tǒng)一起來，方便后面調(diào)用；3）對檢測出有整周跳變的數(shù)據(jù)點，需要查找并恢復(fù)這些跳變。

2 船舶回轉(zhuǎn)運動和航跡的擬合

船舶在航行過程中，為了避讓他船或躲避障礙物，需要通過操舵來改變舵角，從而改變航向。為了研究船舶的航跡擬合曲線和船舶回轉(zhuǎn)運動，船舶操縱運動方程對分析軌跡起到了非常重要的作用。

2.1 船舶操縱運動方程

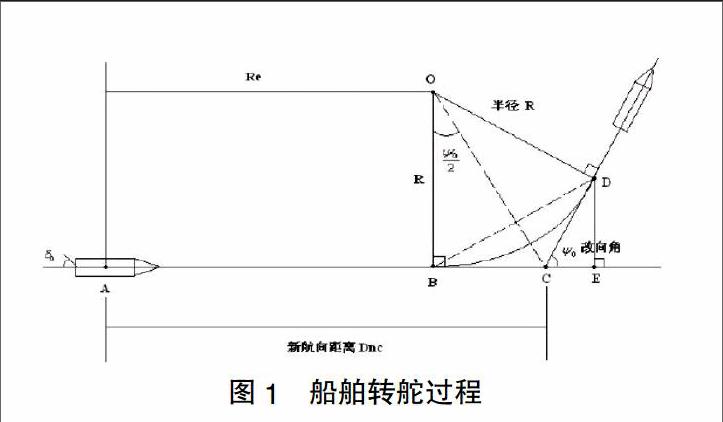
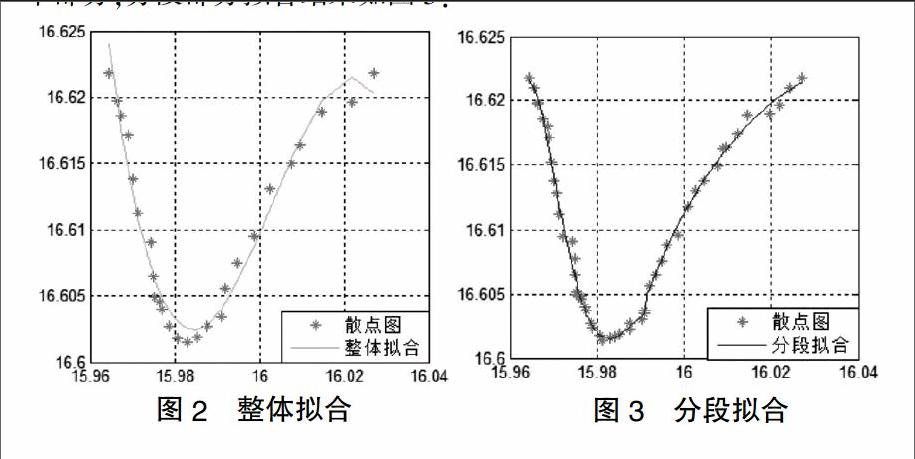
將船舶由操舵產(chǎn)生的各種運動變化看作輸入，輸出為運動變化響應(yīng)關(guān)系，并且在分析Z型操縱實驗的基礎(chǔ)上得到了船舶操縱運動單狀態(tài)變量線性方程：T■T■r+（T■+T■）r+r=K？啄+KT■？啄，其中T1，T2是船舶固有運動響應(yīng)時間常數(shù)，在條件穩(wěn)定的情況下T1，T2為正實數(shù)，且T1，<

該方程反映了船舶操舵角與轉(zhuǎn)向角速度之間的關(guān)系，即船舶一階操縱運動方程。式中r表示船舶轉(zhuǎn)向角速度，r'表示船舶轉(zhuǎn)向角加速度，？啄代表操舵角，K，T系數(shù)是船舶操縱性指數(shù)，分別表示船舶回轉(zhuǎn)性指數(shù)和航向穩(wěn)定性指數(shù)。

2.2 船舶回轉(zhuǎn)運動

航行中的船舶在操舵后進行的運動我們稱之為船舶回轉(zhuǎn)性運動。船舶在回轉(zhuǎn)運動過程中會有一個航跡線的變化過程，圖1是船舶在操舵過程中的運動情況：

船舶在轉(zhuǎn)舵過程中作曲線運動，我們將首向角改變弧度后的軌跡進行近似處理，看作是以R為半徑的圓弧。根據(jù)船舶新航向距離，可以為船舶在何時何地施舵，確保船舶在現(xiàn)在所行的航道上準(zhǔn)確地逐漸行駛到新的航道上，同時根據(jù)船舶新航向距離，以船舶回轉(zhuǎn)運動開始及結(jié)束作為數(shù)據(jù)分段點，模擬船舶航跡。

2.3 航跡擬合

運用最小二乘法三次擬合算法進行航跡擬合得到的軌跡圖誤差相對較大。我們采取先后兩種處理手段：第一，通過增加擬合點的數(shù)量來提高擬合的精確度；第二，采用分段曲線擬合的方法。結(jié)合上文中提到的船舶操縱方程，得出船舶轉(zhuǎn)向角與舵角關(guān)系，并以轉(zhuǎn)舵點為數(shù)據(jù)劃分點，將數(shù)據(jù)分成若干段。為了保證最終的擬合效果達到最佳，該算法必須滿足以下兩點要求：1）為了確保擬合的曲線不出現(xiàn)間斷點，必須保證分段函數(shù)每段的第一個點和最后一個點在擬合函數(shù)上；2）為了保證曲線的光滑性，要保證每段第一個點的導(dǎo)數(shù)值要和前一段最后一個點的導(dǎo)數(shù)值相等。

先設(shè)擬合曲線，求得它的近似值，再求它與實際值的差，可得到殘差的平方和，通過對目標(biāo)函數(shù)展開、轉(zhuǎn)換，最終可以寫成矩陣模式，從而轉(zhuǎn)化為求最小值的問題。考慮到約束條件，對于第一段擬合函數(shù)的約束條件，只需考慮其連續(xù)性即可，對于中間段擬合函數(shù)，約束條件還要加上一個光滑性。

綜上所述，原等式約束的最小二乘法問題被轉(zhuǎn)化成一般形式的二次規(guī)劃問題[7-8]，帶入矩陣數(shù)據(jù)，根據(jù)二次規(guī)劃計算公式以及利用matlab軟件即可得到最優(yōu)解。

3 仿真

通過AIS收集到的船舶經(jīng)緯度信息，然后經(jīng)轉(zhuǎn)換算法轉(zhuǎn)換到高斯平面直角坐標(biāo)系中，進行實驗仿真。具體思路如下，首先會對整體數(shù)據(jù)進行最小二乘法三次擬合處理，如圖2，可以發(fā)現(xiàn)擬合的效果并不是很好，誤差很大，所以接下來會進行增加擬合點數(shù)和分段擬合處理，再對每一部分進行最小二乘法三次擬合處理。根據(jù)上文提到的船舶操縱方程以及船舶轉(zhuǎn)向角速度與舵角的關(guān)系，可以將這組數(shù)據(jù)分成三個部分，分段部分?jǐn)M合結(jié)果如圖3：

從圖2、圖3我們很明顯可以看出，經(jīng)增加擬合點數(shù)和分段處理后的擬合效果要比整體擬合效果好很多，所以本文采用的方法提高了航跡的精確性，更加接近與真實航跡，從而可以分析任意時刻船舶的動態(tài)行為。

4 結(jié)語

本文通過利用AIS收集到的船舶經(jīng)緯度信息將處理后的數(shù)據(jù)進行分段擬合，采用基于最小二乘法三次擬合算法并結(jié)合船舶操縱方程及轉(zhuǎn)向角速度與舵角之間的關(guān)系，將整體數(shù)據(jù)分為三段，分別進行擬合處理，并建立擬合模型。通過矩陣運算將擬合函數(shù)轉(zhuǎn)化為二次規(guī)劃問題，最后通過實驗仿真驗證其有效性。為了提高擬合精度，采取了增加已知點臨近處的點跡作為已知擬合點，擬合結(jié)果表明，本文采用的方法明顯提高了航跡復(fù)原的準(zhǔn)確性，從而能夠更加精確地進行船舶在任意時刻動態(tài)行為的分析。

【參考文獻】

[1]趙森，許振宇，等.地理坐標(biāo)與直角坐標(biāo)相互轉(zhuǎn)換的算法[J].火力與指揮控制，2001，26（4）：64-66.

[2]趙戰(zhàn)興.最小二乘法分段在船舶航跡擬合研究中的應(yīng)用[J].艦船科學(xué)技術(shù)，2016，38（3）：85-87.

[3]張東林.分段最小二乘法曲線擬合[J].沈陽大學(xué)學(xué)報，1994（2）：80-83.

[4]劉健，劉高峰.高斯——克呂格投影下的坐標(biāo)變換算法研究[J].計算機仿真，2005，22（10）：119-124.

[5]熊娟.內(nèi)河船舶航跡擬合與模糊優(yōu)化調(diào)度研究[D].武漢：武漢理工大學(xué)，2013.

[6]周保興.GPS數(shù)據(jù)預(yù)處理方法研究及其應(yīng)用[D].南京：河海大學(xué)，2005.

[7]張春.多項式曲線擬合的計算機解法及應(yīng)用[J].西北水電屯，1993（3）：20-21.

[8]方曼，張尚劍，等.可用于艦船預(yù)測的多項式擬合方法及參數(shù)選擇[J].艦船科學(xué)技術(shù)，2005，27（2）：24-26.

[責(zé)任編輯：田吉捷]