初中數學問題解決的雙向翻譯策略

☉浙江杭州市清泰實驗學校 張娟萍

初中數學問題解決的雙向翻譯策略

☉浙江杭州市清泰實驗學校 張娟萍

數學問題解決是數學教與學的重要組成部分.目前，有大量關于解題技巧和題目類型方面的研究.但是還有很多學生雖能聽懂老師講的例題，但自己解決問題時無從下手，或者同種類型的可以解，變換一下條件就不會了；也有學生對公式、定理滾瓜爛熟，就是不知道什么時候用哪一個.學生更需要問題解決策略的通法指導.

其實，數學問題解決的實質就是一個雙向翻譯的過程.翻譯，通俗地講就是把一種語言文字（源語言）的意義用另一種語言文字（目標語言）表達出來，包括理解、轉換、表達三個環節.在這里，源語言就是指數學問題中的語言表述內容，目標語言則指數學語言.雙向翻譯，包含兩個方面：首先是閱讀源語言，理解分析其含義，將其信息轉換成目標語言；通過數學語言的操作（建模、解模）得到數學結論；然后把數學結論，用一般人所能理解的非數學語言表述出來，從而對實際問題的解決進行解釋.后面部分我們稱之為“回譯”，在回譯時數學結論成了源語言，最后表述的非數學語言變成目標語言.數學問題解決的雙向翻譯，包含以下四個步驟：閱讀—翻譯—建模、解模—回譯.

一、閱讀題目的材料——審題過程

翻譯必然是以閱讀問題為起點的，之所以稱為“閱讀”，而不是“看”，是指有意識地進行觀察，要“領會”材料的意義：把材料敘述的基本內容轉化為條件和目標的形式，弄清已知條件是什么、這些條件之間有什么聯系、有哪些隱含條件等，這就是審題過程.

1.理解題目信息的含義.

數學語言由文字語言、符號語言和圖表語言構成，每一個運算、字符、圖表、點等都具有特定的含義和功能，要咬文嚼字地理解數學材料中這些元素所代表的含義.比如，對于-7×3和（-7）×3，粗看這兩個式子沒有什么區別，只是寫法不一樣罷了，而當你“咬文嚼字”時，就會發現第二個式子比第一個式子多了一個“（）”，進而分析兩個式子的深層次涵義，由于括號是整體的意思，也就是說第二個式子的被乘數是（-7），第二個式子應該理解為“負7與3的積”，而第一個式子沒有加括號，那么被乘數就是7，而前面的“-”又是怎么回事呢？通過思考進一步就會發現這里的“-”是表示“相反的”，那么第一個式子應該理解為“7與3的積的相反數”.這樣，才算真正理解了兩個式子的涵義.

一些數學的關鍵詞如“有”“或”“和”“一定不”“不一定”“不多于”“增長了”“增長到”等，對正確理解材料信息起著很關鍵的作用.

再比如，標點符號“；”，語文中表示“并列”，用“且”“和”“同時”表示，在數學中表示兩個條件并列常以“；”為標志.例如，浙教版七下P46課內練習2：甲、乙兩人從相距36千米的兩地勻速相向而行①.如果甲比乙先走2小時，那么他們在乙出發后經2.5小時相遇②；如果乙比甲先走2小時，那么他們在甲出發后經3小時相遇③.求甲、乙兩人每小時各走多少千米.（以下簡稱“案例”）條件①后面是“.”，表示這個條件是大前提，②與③之間是“；”，表示兩個并列的條件，這樣應該由②與③得到兩個并列的式子，并且都滿足①.

另外，數學材料的語言組織常常有省略現象，所以數學閱讀不像自然閱讀一樣流暢，有時需要將省略的字符進行還原或補充.而且，數學知識具有系統性，新的數學材料中常常包含很多下位知識有關的語言，閱讀時，要提取出這些下位知識.

2.分析語句表達的結構.

要對句子結構包括句子主干、詞與詞的關系、句式進行分析.例如，“幾個相同因數①的積的運算②，叫作乘方③”這一概念，首先可以分析出句子的主干部分是“積的運算叫作乘方”，“幾個相同因數①”是“積”的限定性條件，這樣就可以得出“滿足因數相同①”這一要素的“積的運算②”才是乘方③運算，這樣也有利于理解“積的運算”也就是“乘法運算”與“乘方運算”的關系，得出“乘方運算”是一種特殊的“乘法運算”的深層理解.

還要重視數學表示的特殊句式.數學材料中常見的復合句的句法結構有并列關系和嵌套關系.例如，在“直角三角形①三條邊②的垂直平分線③的交點④是斜邊的中點⑤”這句話中，“直角三角形①”修飾“三條邊②”，二者共同修飾“垂直平分線③”，三者又共同修飾“交點④”，這幾個概念構成三重嵌套關系.

數學表達還跟表述順序有關，如“x與y的平方和”“x與y和的平方”這兩個句子，構成的字母都是相同的，但字母的排列順序不同，使得兩個句子的意義完全不同.

3.標注題目條件的信息.

數學實際問題中相互關聯的信息常常交錯復雜地呈現，閱讀時，要善于從大量的信息中，過濾掉干擾信息，提取有效信息.在有效信息下面劃線標注，突出條件信息，并且在每個劃線條件后面標記序號：一是有利于厘清條件結構；二是方便計條件個數.劃線和標注序號后，在下一步操作（翻譯）時，只要悉數對照序號①②③代表條件的信息，如果解題碰到挫折要重新回到原題時，只要重新審視這些序號所代表的信息即可，避免重復經歷過濾干擾信息等閱讀過程.

比如，浙教版七下P46課內練習2中：第一步：閱讀題目，劃線標出條件信息，并標注序號①②③.“甲、乙兩人從相距36千米的兩地勻速相向而行①.如果甲比乙先走2小時，那么他們在乙出發后經2.5小時相遇②；如果乙比甲先走2小時，那么他們在甲出發后經3小時相遇③.求甲、乙兩人每小時各走多少千米.”

例如，“紅紅兩天看完一本小說①，第一天看了全書的40%②，第二天比第一天多看了15頁③，這本書共多少頁？”

有學生沒有用到“兩天看完①”這個條件，導致問題無法解決、實際上很多學生，在識別出“兩天看完①”和“第一天看了全書的40%②”時，就自動得出“第二天看了全書的60%”（標注‘②’），完成了數學翻譯“引申”的任務.解決問題時，相當于條件是①‘②’③.

在完成全部操作后，仍舊無法解出問題時，要重新審視所有條件，將用到的條件序號劃去，看還剩下什么序號標識條件沒有運用，如這些條件也沒法用上，則要考慮條件的翻譯和變式，有時還需要挖掘隱含的條件將省略掉的內容補充完整，增補序號.

二、翻譯標注的信息——數學化過程

這里的翻譯，是指“雙向翻譯”的前面部分，就是將閱讀時標注的條件信息翻譯成數學語言的過程.

1.根據標注信息翻譯成數學表述.

（1）積累關鍵性詞語的數學表述.

很多學生采用直譯的方式，“直接”按照文字描述的順序逐字“翻譯”，但直譯并不一定能實現正確的數學化.比如，對于“m的2倍比n大1”，表示為“2m比n＞1”.又如，“兩個數互為相反數”，表示為“x=-y”.再比如，“用數學符號表示：負數①的奇數②次方③仍是負數④”，有學生先寫出了奇數②的表示“2n+1”，再寫出奇數次方③的表示“x2n+1”，然后寫出負數①的表示“x＜0”，盡管“負數”“奇數”“乘方”這些要素都表現出來了，但最終不能整體表示出來.反過來，解釋“|x|=-x”的數學意義為：x的絕對值等于負x；解釋“ab=1”的數學意義為：a乘以b等于1.

顯然，“逐字翻譯”，僅僅是將數學符號語言“讀”出來了，并不一定能準確地翻譯成數學語言，所以，需要目標語言對翻譯的導引.平時要積累一些關鍵性詞語與數學運算之間轉譯的表述.如：大于或超出（＞）、不小于或至少（≥）、正數（＞0）、非負數（≥0）；再比如“多、少、增加、擴大、節約”等這些詞對應著數學符號：＋或-；題目中的“幾倍、幾分之幾”常與數學符號×或÷相聯系.

（2）引申條件信息的數學意義.

數學材料中的語言往往是抽象的、形式化的，所以，要對條件信息進一步引申.比如，“今年的總消費比去年減少10%”可引申為“今年的總消費是去年的90%”，翻譯為：今年的總消費＝去年的總消費×90%.

例如，多邊形的概念：由線段①圍成的封閉圖形②叫作多邊形.條件①“線段”解讀為“不能是曲線”，條件②“封閉圖形”解讀為“不能有開口的圖形”，那么多邊形的要素就明確了.

再如，“x的平方與y的差的倒數”，“平方”“差”“倒數”都是名詞，但在翻譯時，必須將它們譯成“運算”，將“平方”翻譯成為乘方運算（自乘二次），將“差”翻譯成減法，將倒數翻譯成“求倒數”.

2.根據條件結構確定表達框架.

面對條件較為復雜的數學問題，根據條件的結構，首先從整體上確定表達的基本結構框架.比如，應用題：G20志愿者人數安排，甲組有40個志愿者，乙組有21個志愿者①，如果要使乙組人數比甲組人數的2倍還多1②，應從甲組調多少人到乙組？解這個題目的關鍵就在“乙組人數比甲組人數的2倍還多1②”這個條件上，“…的2倍還多1”寫成：“2（）+1”.所以，將題目的結構表達出來為：乙組人數=2（甲組人數）+1.

又如，“負數①的奇數②次方③仍是負數④”，根據結論“仍是負數④”可以確定題目的框架是“（）＜0”，再表示（）內部即可.

3.根據條件信息確定結構內部.

（1）框架內部內容的表示.如：奇數②表示為“2n-1”（n為自然數）；奇數次方③表示為“x2n-1”，再表示x是負數①：“x＜0”，最后得出整體表示“若x＜0，則x2n-1＜0”，”.

再比如，“同號兩數相加，取與加數相同的符號，并把絕對值相加.”結合例題（-3）+（-5）＝-（3+5）＝-8，與法則的每一部分進行同步翻譯.第一部分“同號兩數相加”，發現（-3）和（-5）同號，都是負數；第二部分，“取與加數相同的正負號”，所以取“-”；第三部分，“并把絕對值相加”，（3+5），其中，3是（-3）的絕對值，5是（-5）的絕對值.

（2）用未知元和已知量表示相關量.比如，上面的問題中，設從甲組調x人到乙組，則甲組人數：40-x；乙組人數：21+x.代入結構框架“乙組人數=2（甲組人數）+1”中，得到21+x=2（40-x）+1.

回到浙教版七下P46課內練習2中，第二步：將這些條件信息翻譯成數學語言.設甲、乙每小時分別走x千米、y千米.將①甲、乙兩人從相距36千米的兩地勻速相向而行，②甲比乙先走2小時，那么他們在乙出發后經2.5小時相遇，翻譯成數學語言，即4.5x+2.5y=36；將①甲、乙兩人從相距36千米的兩地勻速相向而行，③乙比甲先走2小時，那么他們在甲出發后經3小時相遇，翻譯成數學語言，即3x+5y=36.

“；”表示“并列”，翻譯成數學語言“｛”.

翻譯的過程，自然進入到第三步：使得該問題與方程組建立聯系，問題轉換為解方程組.

根據以上例子我們不難發現：數學問題是一句句有數量關聯的語句構成的，只要我們善于將一字一句譯成式子（方程、不等式、函數式、等式），問題就被簡單地數學化了.

三、對照條件的模型——建模過程

上述翻譯過程，源語言提供的信息與目標語言庫中已有模型進行對照，找到匹配的模型，用數學語言表達出來，就是數學建模.首先，分析條件信息中源語言所對應的基本數學知識點，然后搜索該知識點對應的數學基本模型（假設），通過大腦進行識別和對照，確定模型.比如，水果店以每斤2元的價格購進某種水果若干斤，然后以每斤4元的價格出售①，每天可售出100斤②，經調查發現，這種水果每斤的售價每降低0.1元，每天可以多售出20斤③，水果店決定降價銷售.銷售這種水果要想每天盈利300元④，水果店需將每斤的售價降低多少元⑤？這是關于單價、數量和利潤的問題，腦海中聯想到模型：單（用變量表示）×量（用變量表示）=總，這就是這個題目整體表達的結構框架.然后，用未知量和已知量來表示相關的量，將內部條件結構表示出來，設每斤的售價降低x元，由①、⑤得單利潤：4-2-x；由③得多售出量：0.1x· 20‘③’，由②、‘③’得到銷售量：100+0.1x·20；由④得總利潤為300元.于是得到：（4-2-x）×（100+0.1x·20）=300.這就建立了二次方程.

不同語言之所以可以轉換，是因為：關于同一個知識點的基本模型，不同語言有相應的表征特征.如一次函數不同語言的表征特征如表1所示.

表1

所以，翻譯的關鍵是找到源語言信息中所涉及的基本知識及其對應的基本模型.

文字表述的題目可以直接翻譯成示意圖.例如：“兒子游學今日回，媽媽早到校門口，兒子到后細端詳，母子高興把家還.”如果用縱軸y表示母親與兒子行進中離家的距離，用橫軸x表示母親離家的時間，如圖1，可以選擇第幾幅圖像表達詩意？

圖1

反過來，根據圖形，也可以表示相應的實際信息.

例如，根據圖2，自編一則新的“龜兔賽跑”故事，并寫出龜兔賽跑過程中的函數關系式.這是圖像語言、文字語言和符號語言轉換的典型例子.

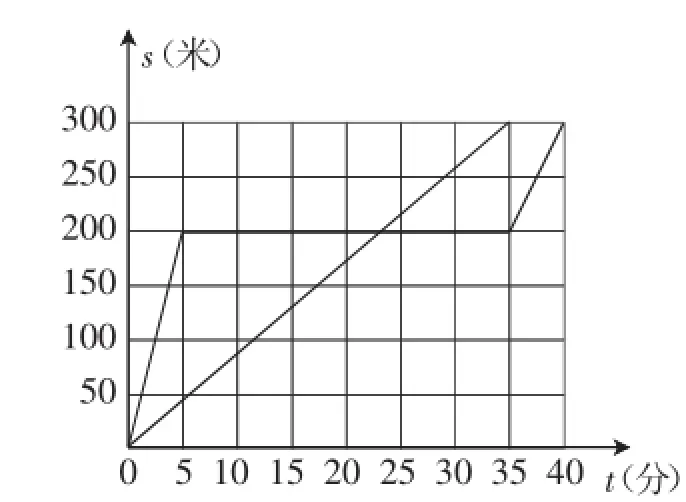
圖2

四、回譯模型的結論——解釋過程

列出模型后，還需解模，就是根據數學知識、技能，解出模型參數的結果.

把參數結果用一般人所能理解的非數學語言表述出來，“從理論分析轉回現實語言”，從而對實際問題的解決進行解釋.這就是回譯，是“雙向翻譯”的后面部分.

回譯首先是檢驗，將模型解得的參數結果代入實際情形進行比較，如果與實際情景吻合，則可以用這個結果來說明實際問題的結果，從而翻譯成實際問題的語言并解釋其實際含義.

浙教版七下P46課內練習2中的問題轉換為解方程組后，根據方程組的解法規則，解得，從而進入第四步：回譯.根據假設“甲、乙每小時分別走x千米、y千米”，把結果翻譯成文字語言，即：甲、乙每小時分別走6千米、3.6千米.

如果模型參數的結果與實際情景不吻合，則要重新回到信息的閱讀、翻譯、建模、解模過程，稱之為“迭代”，經過多次反復“迭代”，直至實際問題結果滿意為止.

1.張嵐.初中生數學學習中自然語言與符號語言的相關性及轉化策略［D］.陜西師范大學碩士學位論文，2008（5）.

2.湯強.7～9年級學生數學符號語言的理解與表示［D］.西南大學博士學位論文，2009（5）.

3.王麗.預設“問題串”漸次推進新知生成——以“有理數乘法”第1課時教學為例［J］.中學數學（下），2016（11）.

4.嚴坤妹.淺談培養和提高學生數學建模能力的對策［J］.福建商業高等專科學校學報，2011（2）.