基于GARCH(1,1)模型的我國商業銀行市場風險研究
李崢

[摘 要]隨著現今金融市場的發展,市場因子的波動性和聯動性也隨之增強。在互聯網金融的時代變革下,商業銀行作為傳統的金融機構,其市場風險管理的重要性由此凸顯。VaR是目前度量市場風險較為成熟的工具,也是巴塞爾委員會一直推薦的市場風險度量方法。以中國農業銀行為例,基于GARCH(1,1)模型對其VaR值進行估計,研究表明VaR可以很好地刻畫商業銀行市場風險。
[關鍵詞]商業銀行;市場風險;VaR;GARCH(1,1)
[DOI]10.13939/j.cnki.zgsc.2017.10.054
商業銀行不可或缺的能力之一是風險管理能力,在承擔風險的同時獲得收益。風險即損失的可能性,商業銀行為了降低這種可能性需要對風險進行高效管理。目前,商業銀行面臨的兩個主要風險是信用風險和市場風險。隨著利率市場化的演進,互聯網金融的變革,商業銀行面臨著前所未有的挑戰,在管理好信用風險的同時,市場風險也成為現今大環境下商業銀行進行風險控制的重要內容。文章以中國農業銀行作代表,運用GARCH(1,1)模型來測算我國商業銀行面臨的市場風險。
1 我國商業銀行市場風險現狀分析
商業銀行的市場風險是指由于市場價格的不利變化,使商業銀行在進行業務時所面臨的風險。這里的市場價格主要包括利率、匯率、商品和股票價格四個部分。一直以來,我國金融市場發展緩慢,商業銀行市場風險管理的可操作性較低,因此,市場風險對我國商業銀行造成的影響十分有限。但現如今,國家政策支持金融市場發展,我國金融市場開始逐步開放,主要體現在利率市場化和匯率市場化兩個方面,由此給我國商業銀行帶來了不穩定的市場環境。
2 VaR方法原理
2.1 “VaR”的定義
用Vt代表一項金融頭寸在時間t的市場價值,L=Vt-Vt-1表示一段時間內金融頭寸的潛在損失。定義VaRα=Var(a;h),在置信水平(1-α)下,VaR定義為P(L>VaRα)=α,即VaRα是在一段置信水平(1-α)下的最大損失,VaR是損失分布函數(1-α)的分位數,即VaRα=F-1(1-α)。
2.2 基于正態分布下的VaR
假設市場變量每天的百分比變化服從正態分布,那么可以簡化VaR計算過程。用正態分布代替一般分布,可得到,VaR=μ+σN-,簡化可得VaR=σN-,其中X為置信水平,對應于展望期的交易組合價值變化的標準法,N-1為累積標準正態分布的反函數上述公式假設均值為0,在考慮市場風險時,通常先計算一天展望期的VaR然后再推算其他展望期的VaR。
2.3 目標區間的選擇
一般來說,銀行在計算市場風險時,通常選擇1天作為目標區間。文章采用現今銀行的一般做法,先計算一天的展望期下的VaR,再計算其他展望期的VaR。基于獨立同分布的假設,T-day VaR=T*1-day。
2.4 置信水平的選擇
置信水平又稱為置信度,是指對樣本進行總體估計時,用概率表達事件結果的可靠度。為了嚴格監管要求,巴塞爾委員會選取了99%的置信度,從而減少銀行因流動性問題導致破產的可能性,從而實現安全穩健的運行。
2.5 VaR的估計方法
2.5.1 歷史模擬法
歷史模擬法是一種非參數方法,它不需要對市場因子的統計分布做出假設,直接根據VaR的定義計算。歷史模擬法的核心在于假定市場因子的歷史變化可以模擬未來損益分布,對損益情況由高到低排序,利用分位數給出一定置信區間下的VaR。
雖然歷史模擬法是最直接、最簡單的計算VaR的方法,但是用歷史去反映未來不符合現實情況,因此,歷史模擬法估計出的VaR誤差較大。
2.5.2 GARCH(1,1)模型
ARCH模型即自回歸條件異方差模型,由ARCH模型延伸出的廣義ARCH模型,即GARCH模型。在測度市場風險時,ARCH模型可以更好地處理金融時間序列數據,即處理異方差和厚尾的能力。目前在市場風險的計量中,GARCH(1,1)模型得到了廣泛的應用。
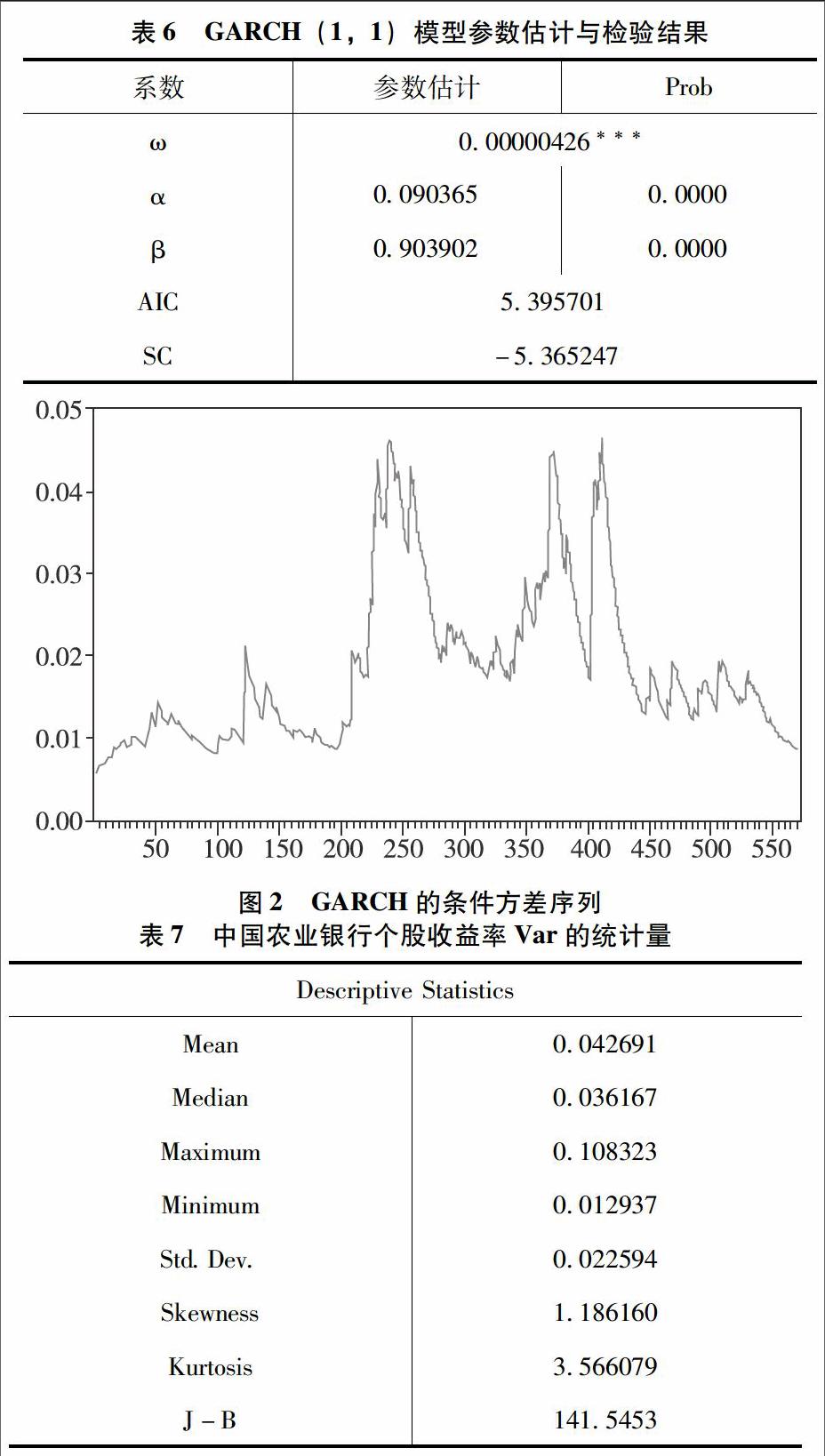
GARCH(1,1)模型的表達式為:σ2n=γVL+αμ2n-1+βσ2n-1,其中,γ對應于VL的權重,α對應于μ2n-1的權重,β為σ2n-1的權重,因為權重之和為1,所以γ+α+β=1,令ω=γVL,可得σ2n=ω+αμ2n-1+βσ2n-1,α+β<1。
3 基于GARCH(1,1)模型的中國農業銀行市場風險測度
3.1 樣本的選取
文章采用中國農業銀行每日收盤價作為研究對象,選中國農業銀行是由于其上市較早,是四大國有銀行之一,具有代表性。本研究時間段從 2014年1月2日至2016年5月6日(觀察值個數為572),時間跨度為三年,數據來源于萬得數據庫。
3.2 基本檢驗
3.2.1 正態性檢驗
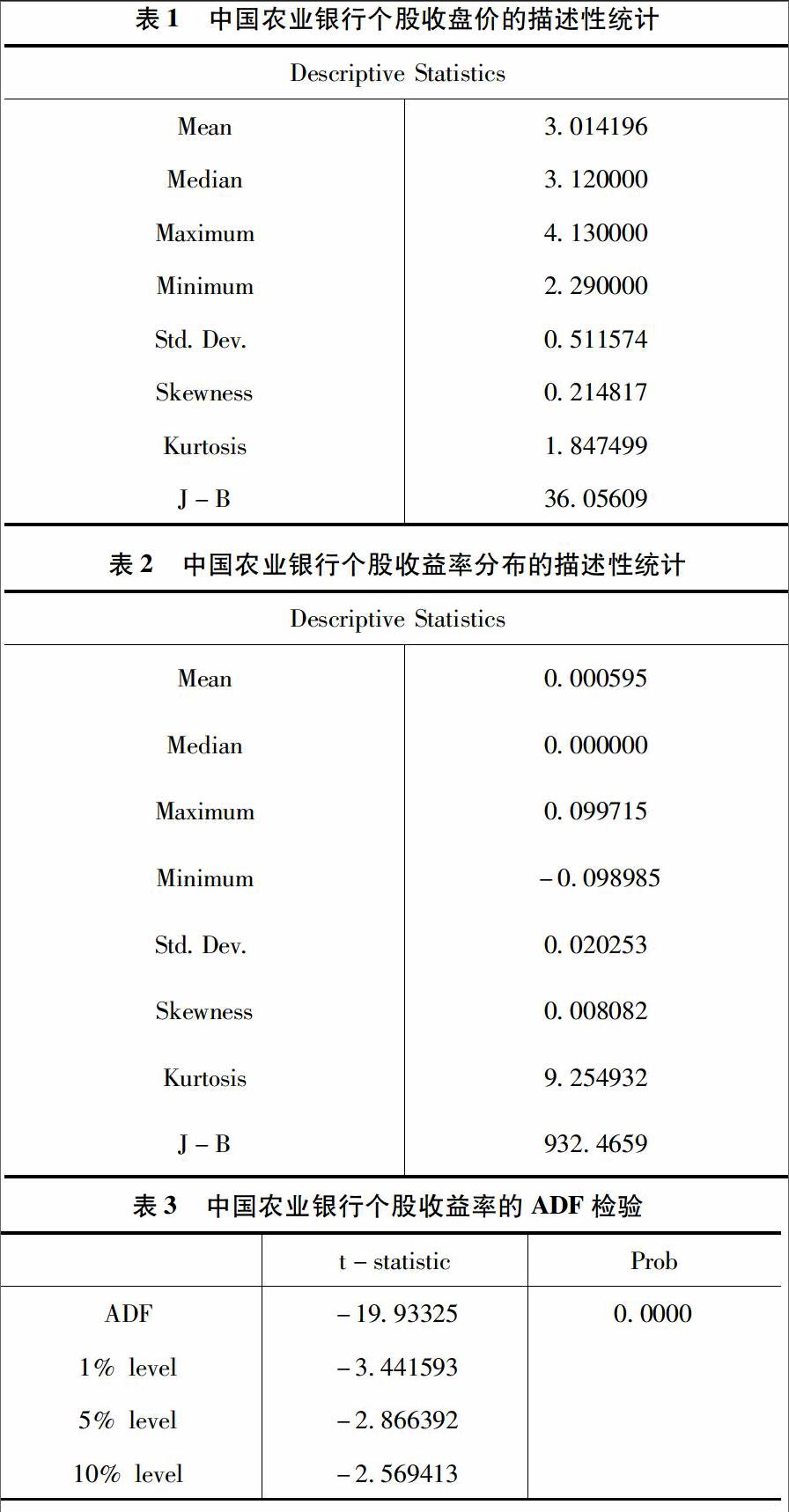
原假設為日收盤價服從正態分布,在正態分布的假設下,Jarque-Bera 統計量(JB 統計量)是服從自由度為2的χ2分布。而檢驗得到的JB統計量=36.05609,大于95%置信水平下的臨界值5.991(P值=0.00),即JB統計位于拒絕域內,認為數據不是正態分布。
3.2.2 收益率分布的正態性檢驗
由表1可知,收盤價不服從正態分布,從偏度(0.214817)和峰度(1.847499)統計量可以看出收盤價是右偏、高峰。
文章采用對數收益率法,對數收益率:lnPt-Pt-1。其中,Pt為當日收盤價,Pt-1為前一日收盤價。對數收益率的正態性檢驗,由表2可知,J-B統計量為932.4659,偏度為0.008082峰度為9.254932。所以,對數收益率不服從正態分布,且具有右偏、尖峰厚尾的特征。
3.2.3 收益率分布的ADF檢驗
表3中,P=0.0000,拒絕原假設,即收益率序列 R 不存在一個單位根,即認為收益率序列是平穩的。
3.2.4 收益率的異方差檢驗
圖1是收益率序列的直線圖,從圖1可以看出,中國農業銀行的日對數收益率存在著明顯的“集群效應”,即認為收益率序列存在著異方差。
4 結 論
VaR 是測度商業銀行市場風險的先進工具,在計算VaR的過程中,需要考慮置信度的選擇、目標區間的設定和市場因素的分布這三個重要因素。文章主要應用GARCH(1,1)模型對中國農業銀行的市場風險進行了測度。
對商業銀行所面臨的市場風險進行控制,最重要的是要有精確的風險識別和度量方法。通過對VaR進行計算,商業銀行可以根據計量結果對市場風險進行有效的識別和度量,對各業務部門進行風險限額管理,從而有效降低銀行市場風險。
與傳統的風險度量相比,VaR有很多優點,它為銀行提供了統一的測度標準,用準確的計量結果刻畫銀行面臨的市場風險。
參考文獻:
[1]Thomas J Linsmerier,Neil D Pearson.Value at risk [J].Financial Analysts Journal,2000(3):47-67.
[2]Franco Bruni,Donald E.Fair.Risk management in volatile financial markets[M].Germany:Springer,1996:184-206.
[3]陳旭輝.基于VaR的我國商業銀行市場風險度量研究[D].長沙:湖南大學,2010.
[4]秦國平.基于VaR的我國商業銀行市場風險計量研究[D].合肥:江西財經大學,2010.
[5]宋濤.基于VaR的商業銀行市場風險度量研究[D].濟南:山東大學,2012.
[6]趙敬.VaR模型在我國商業銀行利率風險度量中的應用研究[D].蘭州:蘭州商學院,2012.

