巧用“三結合”,潤色數學課堂
陳國勇 郭小龍
一、新舊結合。構建支架
在小學階段的數學,很多新知識都可以在已學的知識中找到最近發展區,但是對于學生來說,他們還沒有足夠的能力將新舊知識聯系起來,這時就需要教師及時復習舊知,讓學生將舊知遷移到新知的學習當中,架起新舊知識的橋梁。同時,在學完新知后要讓學生對舊知進行一個全面的回顧,完善所學的知識,讓新舊知識串成一條線,在大腦里形成知識網絡,從而幫助學生成功抵達知識的彼岸。
1.舊知到新知的遷移,激起學習興趣。
舊知是新知的鋪墊,新知是舊知的深入。在數學課堂中,運用好新知與舊知的共同點,加強新舊知識的聯系是非常重要的,這將激起學生學習的興趣,降低學習的難度,提高課堂的學習效率。
執教四上“大數的認識”,這一課要求學習四個計算單位,面面俱到肯定不是最佳策略。我們應該找到新舊知識的連接點,以“十萬”為突破口,引導學生以舊探新,展開積極主動的學習過程。
首先,我們可以選擇生活素材,從復習舊知引入,喚醒學生對舊知的記憶,同時激發學生學習新知的興趣。先展示人口普查數據等能夠充分體現出大數的資料,讓學生感受生活中大數的存在。接著,結合計數器使學生認識計數單位。先從一千一千地數,數到10個一千時,讓學生知道要向萬位進一。再在萬位上一顆一顆地撥,撥到10個時,又要怎么辦?學生自然而然地知道要向前一位進一。這樣的教學,讓學生從舊知到新知的學習有一個正向的遷移,溝通了新舊知識間的聯系,真正做到了“啟”而能“發”1
2.新知到舊知的回顧,加深知識理解。
舊知到新知的遷移固然重要,但是學完新知再回過頭來看舊知也同等重要,它能夠幫助我們建構全面的知識網絡,能夠讓我們以全新的角度重新理解舊知。
在教學人教版四下“乘法分配律”時,筆者在讓學生發現乘法分配律這一規律后,也對知識進行了相應的鞏固。之后筆者設計了一個問題:“在你們之前學過的知識中你知道在哪里有運用到乘法分配律?”學生開動大腦進行思考,發現在學習乘法計算的過程中有用到。一位學生說:“例如在列豎式計算15x12時,12可以看成10+2的和,15x12其實就是15x10與15x2的和。”筆者繼續追問:“再想想,在哪里還出現過?”學生這時出現思維障礙。筆者此時出示一個長方形(長10cm,寬8cm),提問:“長方形的周長是多少?”接著讓2位同學到黑板上展示做法。第一位同學:(10+8)x2=36(cm),第二位同學:10x2+8x2=36(cm)。筆者提問:“請同學們仔細觀察這兩個算式,你發現了什么?”這時,學生恍然大悟,在計算長方形的周長時,實際上已經運用到乘法分配律。借助學習乘法分配律的機會使學生對舊知又有了進一步的理解。
因此,在數學課堂中,教師要合理組織教學活動,在教學的每一個環節注意新舊知識間的聯系,教師要時刻考慮引導學生利用已有的知識促進對新知的學習,同時還要讓學生利用新知加強對舊知的理解。要做到“瞻前顧后”與“邊學邊回頭”,讓已學和新學的知識有機地結合起來,組成一個結構完整的知識體系。新舊知識的結合,將會促進學生思維的提高和發展,也將會讓整個數學課堂得到完美的提升!
二、正反結合。辯證融通
課堂教學永遠是一門有缺憾的藝術。一堂設計再好的課,不同的學生始終會有不同的反應。課堂上的教學資源是處于一個動態生成的過程,既有正確的資源,也有錯誤的資源,教師應該發揮教學機智,善于抓住學生生成的資源,暴露學生的易錯點,突破教學的重難點。課堂上不能為了趕進度而一味地出示正確的資源,也不能一直捕捉錯誤資源而沒有指給學生正確的方向。真正的課堂,應該做到正反資源的有效結合,允許學生出錯,鼓勵學生嘗試,同時也應該給予他們正確的指引。
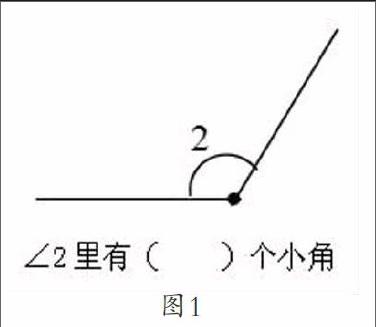
筆者執教四上“角的度量”這一課,在教學進行到用18等分的半圓工具度量角時,設計了一道題目,讓學生動手量。(圖1)
首先展示:量出來有6個小角。學生舉手說:“不同意,因為這個角比直角大,6個小角是錯的。”接著,再讓量出來是12個小角的學生上臺展示,并說出量角的步驟。筆者追問:“剛才那位同學量出來為什么是6個小角,你能幫他分析一下嗎?”學生馬上說:“他數錯方向了,這題中角的邊是和量角器的左邊重合,要從左邊數起。”正反資源的有效結合,讓學生更好地掌握量角的方法。
正確資源的學習能夠得出方法,錯誤資源則更能引起思考。我們應該以全新的觀念,全新的眼光,讓學生在正確中學,在錯誤中成長,將正反加以融合,幫助學生更準確地掌握所學內容,預防錯誤的出現。
三、“基”“能”結合。拓展思維
《課程標準》中明確提出,義務教育階段的數學學習要注重培養學生的“四基”與“四能”。在小學數學的學習中,第一目標就是讓學生掌握好數學的基礎知識,在夯實基礎的同時再來提高和拓展學生的數學思維能力。
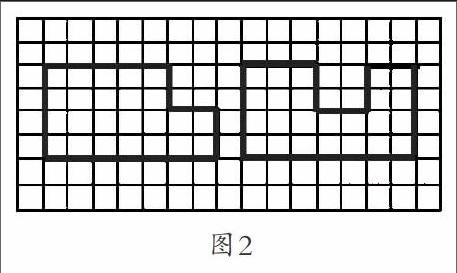
筆者在執教三上“整理和復習:周長”這一課時,主要圍繞“周長在哪里?”與“怎么求周長?”這兩個核心問題幫助學生對所學的周長知識進行梳理,讓他們進一步理解周長的意義。梳理完周長的知識,筆者設計了一道題:比一比,圖2兩個圖形的周長一樣長嗎?(圖中每個小正方形的邊長是1厘米)
此題的設計是在學生對于周長知識掌握牢固的情況下進行的,解決策略可以是采用“數一數”,也可以采用平移的方法。既能夠讓學生掌握基本的方法,又能夠發散學生的思維,他們可以選擇適合自己的方法來解決問題,真正做到在基礎上拓展數學思維。
夯實基礎是根本,提高能力是關鍵。數學課堂不僅僅要讓學生掌握基礎知識,還要提高他們對知識的應用和理解。“基”與“能”的結合,能夠優化課堂教學,提高課堂效果,能夠使數學課堂更具層次性,從而更具“能量”!

