培養學生“論說”·“反思”·“創新”能力的教學探討

江蘇省揚州市邗江區方巷鎮中心中學(225117)

謝 丹●

?

培養學生“論說”·“反思”·“創新”能力的教學探討

江蘇省揚州市邗江區方巷鎮中心中學(225117)

謝 丹●

本文論述了在數學教學中，培養學生“論說”，“反思”，“創新”能力的方法和策略.

數學教學；論說；反思；創新；能力

《數學課程標準》告訴我們：數學教學不僅要考慮教學自身的特點，而且要遵循學生學習數學的心理規律，讓學生親身經歷數學問題的解釋與應用，并能在探索的過程中形成自己的觀點，能在傾聽別人意見的過程中逐步完善自己的想法，實現“不同的人在數學上得到不同的發展”.根據這個觀點在數學教學中要讓學生學會“論學”、“反思”、“創新”，讓學生在數學學習過程中建構自己的數學知識技能，獲得對數學的理解、應用、發展的能力.

一、讓學生學會“論說”

在這里所指的“說”包括：(1)“讀”數學課本“讀”數學問題.通過“讀”讓數學概念和數學問題在學生大腦中有一個初步的印象；通過“讀”讓學生對數學問題有一個感性的認識，從而為上升到理性認識打好基礎.

(2)“說”數學問題中的關鍵字詞(條件)，關鍵數據的含義.每個數學問題中都有該問題的關鍵字詞，讓學生“說”出它，可以看出學生對問題的理解是否已經抓住了重點，有沒有分清主次；“說”關鍵數據，可以讓學生從眾多的數據中梳理出解決問題所需的數據，以及它所代表的量的含義，防止錯用和亂用.

(3)“論說”解題思路，讓學生說出自己的解題思路，從而把他的想法暴露于大家面前，一者可以培養學生敢說的膽量，為以后敢問打下基礎，二者可以讓教師和學生共同發現學生思維的優點和缺陷，從而優化解題思路，三者還可以對該問題的探究可續性提供寶貴素材，提倡提出不同見解可以爭論.

這里所說的“爭論”不是平常所指的吵架，而是指學生在數學思想和方法方面進行的探討和辯論.俗話說：三個臭皮匠頂個諸葛亮.一個班級中一般有學生四、五十個，教師由于年齡、經驗等因素，這個“諸葛亮”往往難免會有失策的地方，而四、五十個“臭皮匠”有時會勝過“諸葛亮”.所以，在課堂教學中，教師要充分發現和利用這樣的機會，讓學生有機會“斗”，通過“斗”讓學生之間互相發現各自薄弱的一面，展示他們的能力和才華，在共同學習中提高數學解決問題的能力.

二、讓學生學會“反思”

解題后，回顧解題過程中所用到的基礎知識，基本技能等，有利于溫故知新，有利于提高分析問題解決問題的能力.

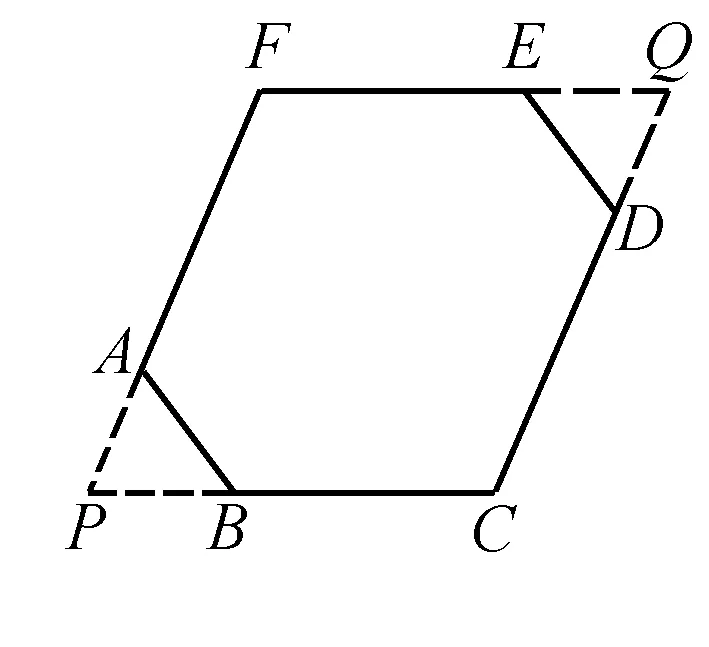
例1 如圖，六邊形ABCDEF中，若∠A=∠B=∠C=∠D=∠E=∠F,且AB+BC=11，AF-CD=3，則BC+DE等于多少？

解析 由已知∠A=∠B=∠C=∠D=∠E=∠F可知這些角均為120°，于是延長FA、CB交于點P，延長FE、CD交于點Q，則得△ABP和△EDQ均為等邊三角形.由∠F=∠C和∠P=∠Q得四邊形FPCQ為平行四邊形，則PA+AF=CD+DQ，即AF-CD=DQ-FA=DE-AB.又已知AF-CD=3，則得DE-AB=3①.又AB+BC=11②，將①、②兩式相加可得BC+DE=14.

反思 本題通過構造平行四邊形并利用平行四邊形的性質得出AF-CD=DE-AB=3，再將其和已知條件AB+BC=11相加，巧妙地得出欲求式子的值.

三、讓學生學會“創”

所謂“創”就是指創新、探究.《數學課程標準》中指出：數學教學要體現現代教育觀念，重視學生創新能力，突出問題解決在數學教學中的重要性….而課堂教學正是讓學生學會“創”的理想場所.當然，作為初中學生雖然獨立思考和探索的愿望和能力均需再提高，但教師作為組織學生“創”的引導者和組織者，首先自己要有“創”的意識，同時有必要給學生提供“創”的條件和素材，在潛移默化中讓學生自己逐步學會“創新”.讓學生學會“創”，可以從以下幾個方面考慮：(1)對于同一問題，讓學生思考能否用其他方法來解決，即我們所說的一題多解即方法上“創”.(2)對于同一問題，改變問題的條件讓學生思考能否得到原來的結論即條件上“創”.(3)對于同一問題，不改變問題的條件讓學生思考能否得出其他結論即結論上“創”.(4)對于同一問題，如果用其他圖形替代原來圖形(如用四邊形替代三角形)，結論又如何？即橫向“創”.(5)對于同一問題，如果改變原來條件或形狀，又能聯想到什么？縱向“創”.

①逆向變形

解分式方程的傳統思想方法是通過去分母或換元把它化為整式方程來解，對于特殊的四次整式方程，也可以反過來化為分式方程來解.

例2 解方程6x4+5x3-38x2+5x+6=0.

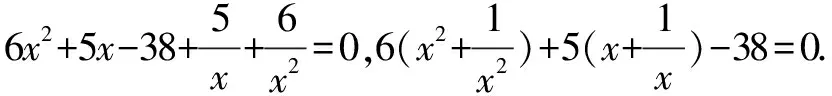
②巧用反證

G632

B

1008-0333(2017)11-0003-01