設計開放性練習，促進學生思維發展

江蘇省南通市通州區四安中學(226352)

管紅星●

?

設計開放性練習，促進學生思維發展

江蘇省南通市通州區四安中學(226352)

管紅星●

練習在學生的學習生涯中必不可少，而且占有重要地位.一個好的數學練習不僅能夠很好地幫助學生掌握知識技能，還能夠有效地活躍學生思維，發展學生各方面才能.課堂教學中，教師要注重開放性練習的設計，以更好地發展學生思維，促使學生高效能發展.

初中數學；開放性練習；數學思維

一、設計多解練習，活躍學生創新思維

在以往的數學練習中，教師所設計的課堂練習有著一定的固定模式，限制了學生的思維空間，不利于學生的深入發展.課堂教學中，教師可以更多地結合實際教學內容，設計一些多解型數學練習，讓學生可以有機會多角度、多思維思考問題，進而更好地活躍其創新思維.

在教學“等腰三角形的性質和判定”時，教師在課堂練習時，為學生設計了一個較為開放的數學練習：一等腰三角形，其中一個角為30度，問該三角形的頂角的度數是多少？很多學生在看到這一問題后，立即想到等腰三角形的兩個底角的度數是相等的這一理論知識，于是很多學生依據三角形內角和180度，列出了一個算式：180-30×2=120.最后得出頂角的度數為120度.此時，學生們對于這一問題的思考也就止于此，認為已經圓滿的解決了這一問題.很明顯學生們忽略了其中的一種情況，只是想當然地認為這里給出的30度的角，描述的是其中的一個底角度數.這時，教師并沒有立即公布這一問題最后的結果，而是繼續提問，讓學生繼續思考：同學們，只有這一種結果嗎？學生們在教師的追問下，意識到這一問題還有其它的結果.于是，開始換思維思考這一問題.隨后，學生想到30度可能就是給出的頂角，所以其頂角可能是30度，還可能是120度.

多解型數學練習的設計，很好地活躍了學生的數學思維，成功地促使學生多角度思考問題，培養了其創新思維，提升了自主學習的效果.

二、設計實際問題，培養學生應用意識

解決實際問題，是學習數學知識的重要目的之一.作為教師要從小培養學生的應用意識，讓每個學生會學以致用.在課堂練習中，教師可以設計一些實際問題，讓學生將所學內容，應用到實際中，以最大限度地激活學生應用意識，發展學生的實踐應用能力.

在教學“一元一次不等式”時，教師引入了一個學生熟悉的數學練習：某商場在臨近春節時舉行促銷活動，并給出了兩種不同的優惠方案：A方案：如果你購買一張168元錢的會員卡，那么你所有購買的商品都將享受8折的優惠.B方案：如果沒有會員卡，那么你所購買的商品將全部享受9.5折的優惠.已知小紅并不是該商場的會員，請你幫小紅計算一下，她在購物時，該選擇哪種購買方案，將會更合算一些.這一問題與學生的生活聯系非常緊密，學生們也都想去解決這一實際問題.學生開始了思考，并結合自己的生活經驗想到，更合算就是所花的錢相對最少.此時，學生們想到自己課上所學的一元一次不等式的內容，想到在這一問題中，必有一個界定值，如果小紅所買的物品原價超過某一值，那么選用其中一種方案較為合適，否則選用另一種方案更為合適.此時，學生開始設自己所買商品的原價為x元，并依據自己所學的不等式的知識列出相應的一元一次不等式：80%x+168>95%x,之后，開始根據自己所學的解一元一次不等式的知識解出最后的結果.發現在不同的價格時，選擇的方案也是不同的.

學生在這一實際練習中，對一元一次不等式的內容有了更深入的認識，并很好地開發了自己的應用思維，鍛煉了其解決問題的能力和應用意識.

三、設計錯誤練習，培養學生糾錯思維

錯誤是學生在學習的過程中不可避免的，每一個錯誤的背后都潛藏著巨大的成功.學生的錯誤點，很多時候是學生的思維的錯誤點，教師要抓住這一點，促使學生更進一步思考發展.教學中，教師可以設計一些學生做錯的練習題，讓學生去尋找錯誤并改正，以更好地培養學生糾錯思維，以及觀察能力.

在教學“分式的乘除”時，教師將學生犯的一些錯誤展示在大屏幕上，讓學生去尋找錯誤，并給予改正.

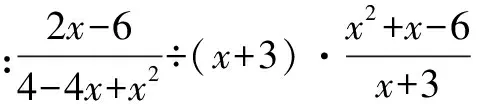
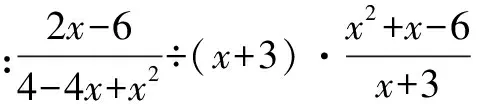
①

②

③

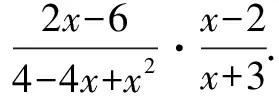
教師通過引出一些錯題，讓學生去探尋觀察，打破以往陳舊的練習模式，極大地活躍了學生的思維，更好地促進了學生有效學習.

總之，練習對于學生的學習意義重大.教師教學中，要注重開放性練習的設計，讓學生借此機會不僅能夠很好的鞏固所學知識，還能夠使其在各方面能力上都能夠得以很好的發展，以充分凸顯數學練習的價值，促使素質教育的實現.

G632

B

1008-0333(2017)11-0034-01