研究解題方法 培養(yǎng)反思習慣

江蘇省揚州市邗江區(qū)陳俊學校(225116)

劉慶金●

?

研究解題方法 培養(yǎng)反思習慣

江蘇省揚州市邗江區(qū)陳俊學校(225116)

劉慶金●

本文強調解題后必要反思養(yǎng)成反思習慣，特別是反思解題方法關于解題方法文中以舉實例詳談了利用判別式法、配方法、換元法、逐步調整法以提高學生的解題能力，培養(yǎng)創(chuàng)新思維.

判別式法；配方法；換元法；逐步調整法

每解完一個數(shù)學題一定養(yǎng)成反思習慣，特別是反思解題方法，就解題而方應追求簡單自然的解法，不必“為技巧而技巧”，舍近求遠.下面就教學實踐中常用的幾種方法舉例研究供參考.

一、利用判別式

利用判別式解整系數(shù)一元二次方程的整數(shù)根問題有下列常見的切入方式：(1)有整數(shù)根的前提是有實數(shù)根，則△≥0，確定參數(shù)的取值范圍；(2)有整數(shù)根必定有有理根，則Δ必為完全平方數(shù)；(3)若判別式是關于參數(shù)的一次式，則可設其為t2(t為非負整數(shù))，再將方程的根用t表示(見例1解法2)).

例1 (“祖沖之杯”競賽題)試求出所有這樣的正整數(shù)a，使得二次方程ax2+2(2a-1)x+4(a-3)=0至少有一個整數(shù)根.

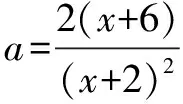
解法2Δ=4[(2a-1)2-4a(a-3)]=4(8a+1)為完全平方數(shù)，故8a+1為奇數(shù)的平方.

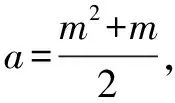
二、配方法

配方法的作用在于揭示式子的非負性，是挖掘隱含條件的有力工具；配方法的實質在于改變式子的原有結構，是變形求解的一種手段，配方法在解代數(shù)式化簡求值、求最值、解不定方程等方面有廣泛的應用.

例2 求方程8(2x2+6x+6)(3y2-3y+2)=15的解(x,y).

分析與解 能展開嗎？不妨應用配方法，從估算兩個因式的值的取值范圍切入.

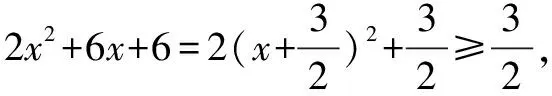
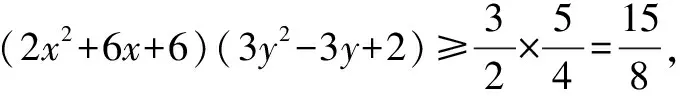
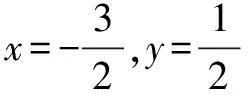
三、換元法

玻利亞在“怎樣解題”表中的許多問句都是以轉換問題為目的，如：你知道與它有關的問題嗎？你能想出一個相同或相似的熟悉問題嗎？你能改述問題嗎？

你能不能用不同的方法重新敘述它？

換元是建立在觀察基礎上的，換元不拘泥于一元代換，可根據(jù)問題的特點，進行多元代換.

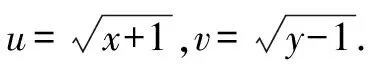
方程②：(u+v)2-2uv=13代入①

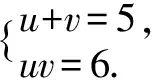
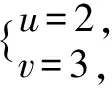
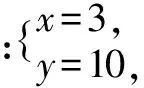
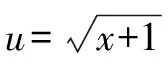
四、逐步調整法

逐步調整法是解離散最值問題的有效方法，即先通過逐步調整變量之間的關系來找出取到最值所需滿足的必要條件，然后再求最值.

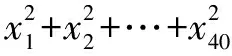
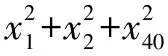
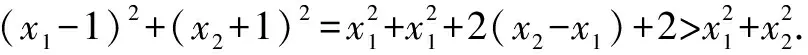
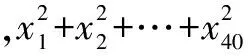
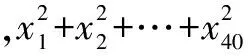
G632

B

1008-0333(2017)11-0005-01