基于三級(jí)供應(yīng)鏈博弈的供應(yīng)鏈決策研究

文/李劉燕

基于三級(jí)供應(yīng)鏈博弈的供應(yīng)鏈決策研究

文/李劉燕

本文是論述以制造商為主導(dǎo)的三級(jí)供應(yīng)鏈系統(tǒng)，在系統(tǒng)中供應(yīng)商、制造商、零售商都在謀求利潤(rùn)最大化。對(duì)于制造商而言，在供應(yīng)商給定的單位產(chǎn)品批發(fā)價(jià)格下，制造商決定單位產(chǎn)品訂貨量和單位定價(jià)去實(shí)現(xiàn)最大化利潤(rùn)，零售商決定產(chǎn)品的訂貨量來(lái)實(shí)現(xiàn)自身利潤(rùn)最大化。通過(guò)三級(jí)供應(yīng)鏈間的博弈的反應(yīng)函數(shù)，來(lái)決定供應(yīng)鏈成員的供應(yīng)鏈決策。

三級(jí)供應(yīng)鏈；博弈；反應(yīng)函數(shù)；供應(yīng)鏈決策

1.引言

2016年，鋼材價(jià)格呈大幅度上漲，從鋼材市場(chǎng)的整體需求來(lái)看，預(yù)計(jì)2017年的鋼材需求相比較于2016年會(huì)放緩增長(zhǎng)。對(duì)于以鋼貿(mào)企業(yè)為軸，供應(yīng)商和零售商為線(xiàn)的三級(jí)供應(yīng)鏈鏈來(lái)說(shuō)，如果在資金有限的條件下，達(dá)到供應(yīng)鏈成員的利益最大化十分重要。

2.基礎(chǔ)模型

本節(jié)將采用Stackelberg博弈模型來(lái)研究該制造商主導(dǎo)的單周期單產(chǎn)品的三層級(jí)供應(yīng)鏈體系，模型的具體假設(shè)如下：

x：是市場(chǎng)對(duì)產(chǎn)品的需求量，其中x＞0；

f（x）：產(chǎn)品需求量的x概率密度函數(shù)；

p：產(chǎn)品的零售價(jià)格，由市場(chǎng)來(lái)決定；

Bm：在訂貨開(kāi)始前，制造商具有的流動(dòng)資金，即制造商的初始資金；

cs：生產(chǎn)單位產(chǎn)品，供應(yīng)商所花費(fèi)的成本；

cm：制造單位產(chǎn)品，制造商所花費(fèi)的成本；

sm：制造商滯銷(xiāo)產(chǎn)品的變現(xiàn)價(jià)值；

gm：制造商單位產(chǎn)品缺貨成本，允許缺貨且不能補(bǔ)貨；

sr：零售商滯銷(xiāo)產(chǎn)品的變現(xiàn)價(jià)值；

gr：零售商單位產(chǎn)品缺貨成本，允許缺貨且不能補(bǔ)貨；

ws：博弈階段供應(yīng)商給定的批發(fā)價(jià)格；

qm：博弈階段制造商公布的訂貨數(shù)量；

wm：博弈階段制造商給定的批發(fā)價(jià)格；

qr：博弈階段零售商公布的訂貨數(shù)量；

πs，πm，πr：分別為供應(yīng)商、制造商、零售商利潤(rùn)函數(shù)；分別為供應(yīng)商、制造商、零售商的期望函數(shù)。

在該模型中假定產(chǎn)品需求的密度函數(shù)f（x）是均勻分布的，且分布區(qū)間為[0，b]，此時(shí)有f（x）=1/b。[4]

遵從市場(chǎng)運(yùn)行規(guī)律，本文供應(yīng)鏈間的stackelberg主從博弈系統(tǒng)為：供應(yīng)商、制造商和供應(yīng)商，且該系統(tǒng)的博弈順序?yàn)椋海╥）由擁有更多主動(dòng)權(quán)的供應(yīng)商首先公布其給定產(chǎn)品的批發(fā)價(jià)格ws；（ii）再由制造商在得到準(zhǔn)確價(jià)格后，根據(jù)自身利益最大化原則確定訂貨量qm及給零售商發(fā)布定價(jià)wm；（iii）零售商得到制造商給定的價(jià)格后，根據(jù)自身利益最大化原則確定訂貨數(shù)量qr。在這個(gè)系統(tǒng)中，假定都是理性參加且在決策過(guò)程中兩兩之間都了解對(duì)方的成本及利潤(rùn)等相關(guān)信息。

3.三級(jí)供應(yīng)鏈博弈

對(duì)于日漸回暖的鋼材銷(xiāo)售量，制造商面臨的主要問(wèn)題是：有資金約束和沒(méi)有資金約束，且當(dāng)制造商面臨資金問(wèn)題時(shí)不能得到外部的幫助。在基于stackelberg模型的訂貨過(guò)程中，制造商是通過(guò)先預(yù)測(cè)零售商的反應(yīng)函數(shù)制定出使自身利潤(rùn)最大化的最優(yōu)批發(fā)價(jià)格，同理，供應(yīng)商也是通過(guò)制造商的反應(yīng)函數(shù)來(lái)制定是自身利潤(rùn)最大化的最優(yōu)批發(fā)價(jià)格制造商根據(jù)供應(yīng)商提供的最優(yōu)批發(fā)價(jià)格wm*來(lái)確定自身的最優(yōu)訂貨量。

受到初始資金影響時(shí)制造商的期望利潤(rùn)函數(shù)為：

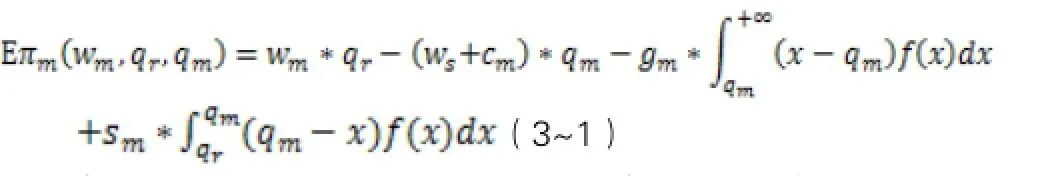
將f（x）=1/b（0≤x≤b）代入到式（3～1）中，可得制造商的期望利潤(rùn)為：

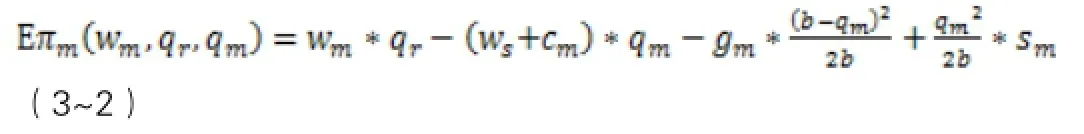
供應(yīng)商所面臨的問(wèn)題是：

命題在考慮制造商資金問(wèn)題時(shí)，供應(yīng)商的stackelberg博弈均衡解為：

制造商的stackelberg均衡訂貨量為：

證明：分別對(duì)資金充足和資金不足時(shí)做出證明，證明如下，

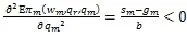
②當(dāng)制造商的資金受到約束時(shí)，

綜上可得，制造商的反應(yīng)函數(shù)為：

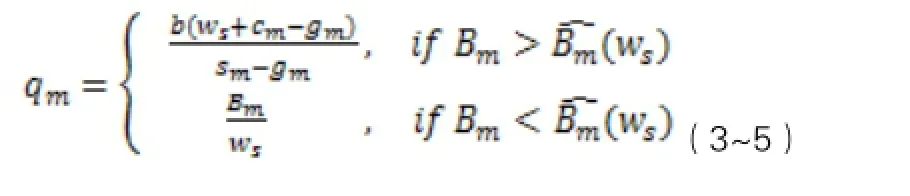
對(duì)式（3～6）求關(guān)于ws的二階導(dǎo)數(shù)，

很明顯，Eπs（ws）是關(guān)于ws增函數(shù)。供應(yīng)商按照利潤(rùn)最大化原則，應(yīng)制定的批發(fā)價(jià)格按照來(lái)供貨給制造商。相對(duì)的，制造商也會(huì)根據(jù)其反應(yīng)函數(shù)得到的的最佳訂貨量。

4.供應(yīng)鏈決策

綜上所述可以得到關(guān)于供應(yīng)商給出的批發(fā)價(jià)格（ws）和制造商的訂貨量（qm）的結(jié)論：

制造商面臨的界限就是在使得自身利益最大化的同時(shí)一定要具備足夠的資金。

在沒(méi)有任何約束條件下，將f（x）=1/b帶入到（4～1）中，零售商的期望利潤(rùn)函數(shù)為：

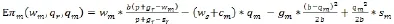
對(duì)上式求關(guān)于wm的二階導(dǎo)數(shù)，

5.結(jié)束語(yǔ)

三級(jí)供應(yīng)鏈博弈對(duì)于供應(yīng)鏈成員的供應(yīng)鏈決策有普遍意義。供應(yīng)鏈成員從自身利益最大化的角度，判斷下游企業(yè)的反應(yīng)函數(shù)，然后再結(jié)合自身的期望利潤(rùn)函數(shù)來(lái)作出最合適的企業(yè)決策是非常有必要且深化的。學(xué)者還可以嘗試在資金約束下且引入供應(yīng)鏈金融后，再通過(guò)博弈模型分析，研究供應(yīng)鏈決策。

（作者單位：北京物資學(xué)院）

[1]李柏勛，周永務(wù)，曾偉.多供應(yīng)鏈間的Nash和Stackelberg博弈決策模型[J].工業(yè)工程，2011（06）：10～15

[2]張畢西，王文龍，張明珠，于秀麗.三級(jí)供應(yīng)鏈間stackelberg博弈分析[J].數(shù)學(xué)的實(shí)踐與認(rèn)識(shí)，2015（15）：154～163.

[3]鐘遠(yuǎn)光，周永務(wù)，李伯勛，王圣東.供應(yīng)鏈融資模式下零售商的訂貨與定價(jià)研究[J].管理科學(xué)學(xué)報(bào)，2011，14（6）：57～65.

[4]李娟.基于供應(yīng)鏈金融的供應(yīng)鏈行為決策研究[D].南京：南京大學(xué)，2014.

[5]鐘海巖，徐長(zhǎng)冬，任曉婷.三級(jí)供應(yīng)鏈的利潤(rùn)分配策略研究[J].商場(chǎng)現(xiàn)代化，2014（06）：27～28.

[6]藍(lán)永泉.供應(yīng)鏈管理中的若干斯坦克爾伯格博弈問(wèn)題研究[D].合肥：中國(guó)科學(xué)技術(shù)大學(xué)，2013.

[39]鐘海巖，徐長(zhǎng)冬，任曉婷.三級(jí)供應(yīng)鏈的利潤(rùn)分配策略研究[J].商場(chǎng)現(xiàn)代化，2014（06）：27～28.