利用“數學工具”探索數學問題解決教學模式初探

羅海霞

摘要：問題解決是數學課程培養的核心素養之一。從中職生的數學學習特點出發，充分挖掘數學工具輔助學生解決數學問題的作用，探索問題解決教學模式的主要特征、教學程序及評價方法等。

關鍵詞：教學模式；問題解決；數學工具

中圖分類號：G712 文獻標志碼：A 文章編號：1673-9094-（2017）02/03C-0018-04

“數學工具”指數學教學過程中，為更好地促進并達成學習目標所采用的工具，主要指數學軟件或數學辭典等。本課題指幾何畫板、計算器、EXCEI等較為普及的數學教學軟件。這些教學軟件具有強大的計算、作圖、列表、動畫、演示等功能。“在講抽象的概念之前，運用計算機和數學軟件的計算、演示、模擬功能，讓學生自己去分析、發現其中的規律，在真正講授抽象概念時，就不會感到突然。在講述定理時，也可以參照這個辦法。在計算機的幫助下，可以將以往繁重的、手工不能實現的計算變得輕松起來……這樣就可以將實際問題引進課堂，讓學生體會數學的實際價值”。研究證明，數學工具可以彌補學生抽象思維能力的不足，讓他們在動手實踐的過程中理解知識、應用知識，從而促進他們利用數學工具進行計算、思維和應用的能力。據此，筆者嘗試在中等職業學校開展利用數學工具的教學，并根據中職生的認知特點和教學規律，構建起問題解決教學模式。

一、數學工具輔助學生問題解決學習的可能性

問題解決教學的教育價值在于培養學生學會觀察、分類、概括、歸納、一般化、特殊化、分析解決問題的思維能力，運用原有的知識和經驗解決新的陌生的問題。《中等職業學校數學課程標準》明確指出：“培養學生運用計算器、計算機進行計算的能力……學會分析問題、解決問題的問題解決的能力”。新的課標要求充分明確數學工具的功能與價值。我們不能再簡單滿足于用幾何畫板研制個別課例，或將計算器、EXCEL的部分操作案例僅僅作為教材的附錄加以介紹，而需要利用數學工具引導中職生開展問題解決教學，并逐步構建有效的教學模式。

中職生大部分是怕學數學的，具體表現在“認知障礙、記憶障礙、閱讀障礙、運算障礙”等方面的困難，一部分學生“多動、分心、固執、笨拙、沖動、孤僻”的行為特征也不利于學好數學。心理學家沃納認為“處于這種狀態的學生，往往在數學學習方面表現出審題能力差，抽象思維能力薄弱，空間認知能力低，記憶力低，導致的運算障礙等”。針對這樣的學生“在學力補救中，將教學方式結構化（從個別教學到小組教學），使學生大量體驗自我表達及和別人進行問答的習慣”。

問題解決學習具有在教學方式結構化的情境中開展學習的特點。問題解決學習起源于20世紀50年代美國的醫學教育。它的原型基本特征有五個方面：（1）將學生分組；（2）組內對問題進行研究和討論學習；（3）學生進行自我指導；（4）再次集合匯報各自學習心得，并處理問題；（5）學生對自己的工作進行自評和組評。通過問題解決對數學知識形成深刻的、結構化的理解，形成問題解決的技能，發展自主學習能力。問題解決是貫穿學習始終的核心，主要特征包括目的指向性；心理過程的一系列操作序列為了達到某種終結狀態，而采用的認知操作過程。

同時，我們也應該警惕問題教學在實踐中的不足，“忽略操作的作用而總是保持在語言水平上，特別在數學教育中這是一個嚴重的錯誤……操作和數學實驗遠非阻礙了演繹思想的后期發展，事實上它組成了一個必要的準備”[5]。因此使用數學工具是為了達到目的而選擇的操作手段，是認知操作過程的一部分，是認知操作手段的延伸和拓展，是進行問題解決學習不可或缺的工具。數學工具在輔助問題解決學習中具有以下特點：第一，形象性。借助數學工具可以形象地展示數學概念、規律。第二，實時性。數學工具可以隨時根據學習的需要展示數學對象。第三，替代性。數學工具可以替代中職生開展計算、作圖、制表等工作。

二、中職生使用數學工具進行數學問題解決學習的基本程序

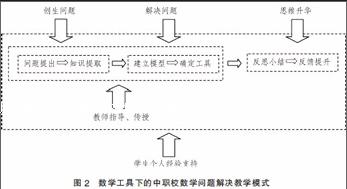
“數學問題解決教學是通過創設問題情境，激發學生的求知欲望，使學生親身體驗和感受分析問題、解決問題的全過程。它強調使用數學的意識，培養學生的探索精神、合作意識和實際操作能力。”運用數學工具進行問題解決教學程序包括以下六個環節。

（一）基于問題解決的教學設計

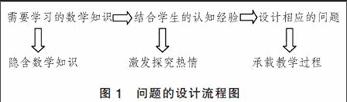
問題解決在問題空間中進行搜索，由一定的情景引起的，按照一定的目標，應用各種認知活動、技能等，經過一系列的思維操作，使問題得以解決的過程。問題的設計是整個教學過程的關鍵。所提出的問題既要激發學生的學習興趣，又要包括即將學習的數學知識，且能引導學生自主探究不斷深入。關于問題的設計流程如下圖：

圖1 問題的設計流程圖

（二）數學知識的應用準備

數學知識包括數學的概念、公式、定理、運算方法等。此處的知識傳授，有別于傳統的教學模式，通過反復訓練，強化知識認知。這樣的模式固然強化了基礎，然而卻犧牲了學生的問題意識、創造思維和應用能力的培養。本模式則強調通過問題的引導，教師指導學生經過查找、思維等過程，親身體會知識產生的過程，這樣的學習具有靈活性和可變通性。

（三）建立問題解決數學模型

數學模型（Mathematical Model）是將現實問題歸結為相應的數學問題，并在此基礎上利用數學的概念、方法和理論進行深入的分析和研究，從而從定性或定量的角度來刻畫實際問題，并為解決現實問題提供精確的數據或可靠的指導。通常用字母、數字及其它數學符號建立起來的等式或不等式以及圖表、圖像、框圖等描述客觀事物的特征及其內在聯系的數學結構表達式。建立數學模型就是溝通現實問題和數學知識、數學工具的必要途徑。

（四）確定數學工具和操作路徑

當建立在數學知識基礎之上的數學模型一經確立，解決這個模型對應的問題，需要學生尋找合適的數學工具。如模型是二次函數最值問題，可以選擇幾何畫板中的作圖工具，很容易地獲得結果。而無需運用二次函數圖像法求最值或配方法求最值，因為這些方法對于多數中職生是難以理解的，更無從運用它們解決問題。借助工具，不僅可以幫助學生克服因解決數學模型帶來的思維障礙，更可以幫助學生順利地發展建模思維。