小改編，大不同
——一道課本習題的改編歷程

廣東省惠州市惠陽區沙田中學 張 貝

小改編，大不同
——一道課本習題的改編歷程

廣東省惠州市惠陽區沙田中學 張 貝

一、改編題的來源

初中數學教材中有許多習題都蘊含著重要的數學思想和方法，對數學解題具有一定的導向作用，每一道課本習題都是經過編者不斷推敲﹑揣摩的，蘊含著他們大量的心血。課本習題的教學是鞏固學生雙基﹑培養學生思維能力﹑提高學生解題能力的一條重要渠道，教學中，我們要善于對習題進行合理的變化和挖掘，我們將其改編是豐富原題內涵的有效途徑，同時，在教學中將教材中的典型例題進行改編，既能夠激發學生的學習興趣，又能培養學生發現問題和解決問題的能力。我查找了平時教學中積累的典型習題，查閱了相關資料及近幾年各地的中考題，特別是廣東近幾年的中考題，它們都是進行改編題的第一手資料。我最終選擇以下習題進行改編，原題選自人教版《數學》（2009年3月第2版）九年級上冊第24章第123頁第14題。

原 題： 如 圖1， ⊙O的 直 徑AB=12cm,AM和BN是它的兩條切線，DC切⊙O于E，交AM于D，交BN于C。設AD=x，BC=y，求y與x的函數關系式，畫出它的圖象。

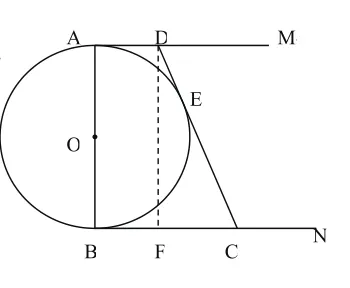
圖1

分析：本題以學生熟悉的圓與直角梯形為知識載體，主要突出對本章所學的核心概念（切線）和數學定理（切線性質及切線長定理）進行考查，涉及的知識點是最基礎﹑最核心的數學知識。特別是圖中所需的輔助線的構建，對發展學生的抽象思維，借助數學直觀提煉基本圖形所隱含的性質和結論有著重要的作用。

二、改編歷程

1.初稿

如圖2，⊙O的直徑AB=12cm,AM和BN是它的兩條切線，DC切⊙O于點E，交AM于D，交BN于C,設AD=x，BC=y。

（1）求y與x的函數關系式；

（2）用含x的式子表示求圖中陰影部分的面積S。

解：（1） 如 圖 2， 過 點 D作DF⊥BC于點F，

∵AM和BN是⊙O的兩條切線，DC與⊙O相切,

∴AD=DE=x,BC=EC=y,

在Rt△DFC中， ,

圖2

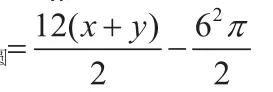
反思：課本習題考查的知識點較單一，綜合性不強。改編后的題在圖形上沒有多大的變化，只是再添加了陰影部分，條件上沒有增加新的條件，只是簡單增設了一問。此題較原題就考查內容上有所豐富，增加考查了不規則圖形的面積求法，涉及的知識點多，體現了一定的層次性針對。針對增加的第（2）問，在解答時發現，第（1）問為第（2）問解答做了鋪墊，降低了題目的難度，使不同層次的學生的思維都得到了鍛煉。習題中設問（1）（2）之間采取的是遞進式的結構，采用遞進式的結構能挖掘問題的深度。

2.磨稿

改編稿1：

如圖2，⊙O的直徑AB=12cm,AM和BN是它的兩條切線，DC切⊙O于點E，交AM于D，交BN于C,設AD=x，BC=y。

（1）求y與x的函數關系式;

（2）用含x的式子表示圖中陰影部分的面積S;

（3）當x，y滿足何種關系時，S取得最小值？并求出最小值。

解：（1）如圖2過點D作DF⊥BC于點F，

∵AM和BN是⊙O的兩條切線，DC與⊙O相切,

∴AD=DE=x,BC=EC=y,

在Rt△DFC中，

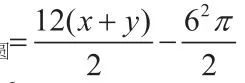
反思1：此題在初稿的基礎上增加了一問，增加的第（3）問讓問題的設計變得更加有梯度，起到了引導學生思維的作用，增加的這一問仍然采取的是遞進式的結構，巧妙地借助了設問（1）（2）的結論來解答，但美中不足的是在解（3）的時候用到了均值不等式，而這個內容在初中階段來說是有超綱之嫌。

改編稿2：

如圖2，⊙O的直徑AB=12cm,AM和BN是它的兩條切線，DC切⊙O于E，交AM于D，交BN于C,設AD=x，BC=y。

（1）求y與x的函數關系式；

（2）用含x的式子表示圖中陰影部分的面積S。

（3）連接BE,當x為何值時，△BCE為等邊三角形？并求當△BCE為等邊三角形時圖中陰影部分的面積。

解：（1）過點D作DF⊥BC于點F，

∵AM和BN是⊙O的兩條切線，DE與⊙O相切，

∴AD=DE=x,BC=EC=y，

在Rt△DFC中， ，

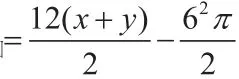
（3）連接OE,過點O作OG⊥BE。

∵△BCE為等邊三角形，∴∠EBC=60°，∴∠OBG=30°，在Rt△OGB中,

反思2：因為在改編稿1中的第（3）問存在超綱的嫌疑，所以在改編稿2中我否定了這種設問，再次改編后的（3）能夠與（1）和（2）有更加緊密的聯系，圍繞著初中數學中常見﹑常考的等邊三角形這個知識點，改編稿2繼續進行著遞進式結構，緊緊圍繞著中考考綱，盡可能全面地考查學生的知識結構和能力。

總之，課本習題是編者精心設計和挑選的，具有典型性和探索性，所隱含的內容也相當豐富，現在很多中考題都能在課本中找到其原形。因此在教學中，教師要重視教材，吃透教材，鉆研教材，加強對課本習題的挖掘，靈活使用習題，通過一題多變﹑一題多解把問題弄透，達到觸類旁通﹑舉一反三的效果，從而進一步提高學生的解題能力和探究能力，使教學達到“事半功倍”的效果。

book=93,ebook=95