化“折”為“直” 巧解最值

王學(xué)俊

化“折”為“直” 巧解最值

王學(xué)俊

轉(zhuǎn)化思想是一種最基本的數(shù)學(xué)思想，用于解決問題的基本思路是：化未知為已知，把復(fù)雜的問題簡單化，把生疏的問題熟悉化，把非常規(guī)的問題常規(guī)化，把實際問題數(shù)學(xué)化，實現(xiàn)不同的數(shù)學(xué)問題間的相互轉(zhuǎn)化，這也體現(xiàn)了把不易解決的問題轉(zhuǎn)化為有章可循、容易解決的問題的思想.

【探索活動】

引例：如圖1，在一條小河l（小河的寬度忽略不計）的兩側(cè)有兩個村莊A、B，在小河邊修一碼頭P，使PA+PB和最短.

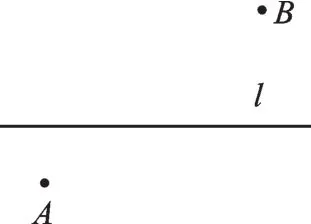
圖1

圖2

【分析】可能你不難發(fā)現(xiàn)動點P的位置，連接AB與l的交點即為點P，如圖2.因為兩點之間線段最短，求“共點折線”（有公共端點的折線段）的最值問題，把“折線”轉(zhuǎn)化為“直線”是解決這一類問題的基本模型.

變式：如圖3，若兩個村莊A、B在小河l的同側(cè)，在小河邊修一碼頭P，使PA+PB和最短.

圖3

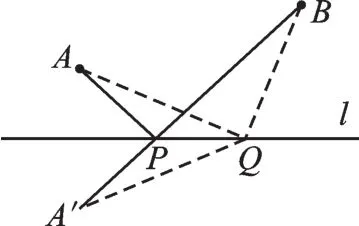
圖4

【分析】這也是一道求“共點折線”的最值問題，但與上題的不同之處在于：兩定點位于動點所在直線的同側(cè).如圖4，利用對稱性把同側(cè)問題轉(zhuǎn)化為兩側(cè)問題，且可保證動點P到A、A′的距離相等，要求PA+PB和最短，只要求PA′+PB和最短，這樣，化“折”為“直”即可解決.

【提煉方法】

求“共點折線”的最值問題方法：

（1）若兩定點在動點所在直線的同側(cè)，利用對稱性，把同側(cè)問題轉(zhuǎn)化為兩側(cè)問題；

（2）通過化“折”為“直”來巧解最值.

【知識運用】

一、兩折線問題

例1 如圖5，正方形ABCD的邊長是4，點P是CD上一點，且DP=1，Q是對角線AC上任一點，求：QP+QD的最小值.

圖5

圖6

【分析】求動點Q到兩定點D、P的距離和的最小值，就是求“共點折線”的最值問題，你能從復(fù)雜的圖形中找到熟悉的原型嗎？

【解題思路】

（1）化同側(cè)為兩側(cè)：如圖6，找到點D關(guān)于動點Q所在直線AC的對稱點B；

（2）化“折”為“直”：連接BP，線段BP的長即為QP+QD的最小值.

因為在Rt△BCP中，BC=4，CP=3，所以BP=5，即QP+QD的最小值為5.

變式：如圖7，在銳角△ABC中，AB=4，∠BAC=45°，∠BAC的平分線交BC于點D，M、N分別是AD和AB上的動點，求：MN+BM的最小值.

圖7

【分析】這是一道求“共點折線”的最值問題，與之前有所不同的是：點N也是一個動點.要將其轉(zhuǎn)化為所學(xué)的方法解決，必需化“動”為“定”，可先將點N看成一個定點來解決.

【解題思路】

（1）化“動”為“定”：先把動點N看成定點，利用化“折”為“直”找到線段和的最小值.如圖8，作點B關(guān)于AD的對稱點B′，連接B′N，線段B′N的長即為MN+BM的最小值.

（2）再把點N看成動點，當(dāng)點N運動到B′N⊥AB時，線段B′N的長度最小，如圖9.這樣問題就轉(zhuǎn)化為求一點B′到線段AB的距離.

圖8

圖9

因為AB=4，所以AB′=4，

在△ANB′中，∠ANB′=90°，∠BAC=45°， sin45°=NB′∶AB′，∴B′N=22，即MN+BM的最小值為

【題后反思】求“共點折線”的最值問題，要能從復(fù)雜的圖形中找到熟悉的原型，從而把復(fù)雜問題簡單化.若兩定點變?yōu)橐粍右欢〞r，可將動點看成定點，把非常規(guī)問題常規(guī)化.

二、三折線問題

例2 如圖10，在平面直角坐標(biāo)系中，A（1，3），B（4，1），在x軸上找一點M，在y軸上找一點N，使四邊形ABMN周長最小，求點M、N坐標(biāo).

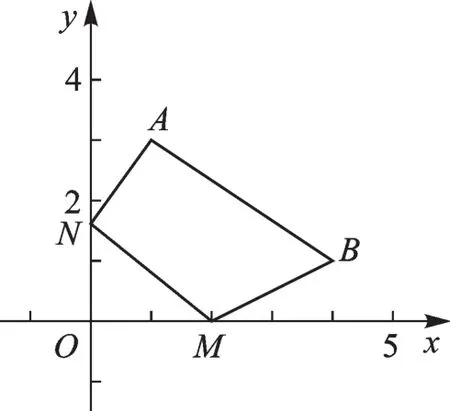
圖10

【分析】圖中A、B為定點，M、N為動點，所以AB長度為定值，要使四邊形周長最小，只要AN+NM+MB和最小，這是一道“三折線”和最小問題.要想用所學(xué)的知識來解決，必需遮擋住其中一條折線，使其轉(zhuǎn)化為“兩折線”問題，找出表示兩折線和的最小線段，再求出與第三條折線和的最小值.

【解題思路】

（1）化“三折”為“兩折”：遮擋住其中一條線段，如圖11，把點M看成定點，線段A′M長即為AN+NM和的最小值.

（2）再求A′M+MB和的最小值，如圖12，線段A′B′長即為AN+NM+MB和的最小值.

（3）要求M、N點的坐標(biāo)，可先求出直線A′B′的函數(shù)關(guān)系式，再求它與坐標(biāo)軸的交點.

圖11

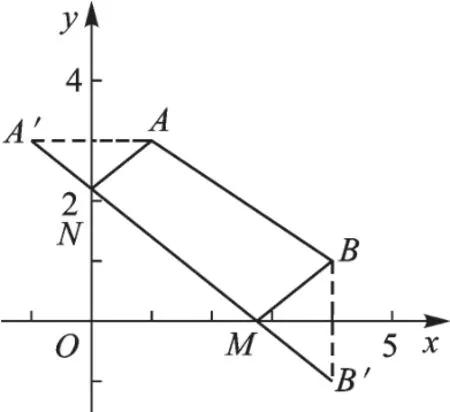
圖12

由對稱可知：A′（-1，3），B′（4，-1）.

【題后反思】求“三折線”和最小問題，我們可以遮擋一部分，將其轉(zhuǎn)化為熟悉的“兩折線”問題求解，再依次求解.以后遇到多折線都可以用這方法.

變式：如圖13，在平面直角坐標(biāo)系中，A（1，3），B（4，1），在x軸上有兩點C（a，0），D（a+2，0），當(dāng)a為何值時，四邊形ABDC周長最小.

圖13

【分析】圖中A、B為定點，所以AB長為定值，這也是一個“三折線”和最小問題，但從C、D坐標(biāo)可看出CD=2，要使四邊形周長最小，只要AC+BD和最小.這與“共點折線”不同的是，這兩條線段沒有公共端點.要想用所學(xué)知識來解決，就要使兩條線段有公共端點，可以通過平移變換將其轉(zhuǎn)化為“共點折線”來解決.

【解題思路】

（1）將兩線段轉(zhuǎn)化為“共點折線”：如圖14，將點B水平向左平移2個單位，連接CB′，即得到CB′=DB，AC+BD=AC+B′C；

（2）如圖15，當(dāng)AC+CB′的和最小時，確定點C的位置；

（3）求出直線AB″的函數(shù)關(guān)系式與x軸的交點即為點C坐標(biāo).

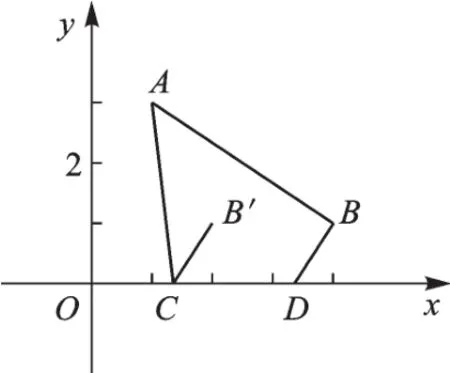
圖14

圖15

因為B（4，1），所以B′（2，1），B″（2，-1），

直線AB″的函數(shù)關(guān)系式是y=-4x+7，

【題后反思】若兩線段無公共端點，要求它們和的最小值，可先通過平移將其轉(zhuǎn)化為“共點折線”，再化“折”為“直”來求和的最小值.

在解決上述問題的過程中，我們應(yīng)用了化“折”為“直”、化“動”為“定”、化“三折”為“兩折”等方法，充分體現(xiàn)了用轉(zhuǎn)化思想解決問題的基本思路，也體現(xiàn)了把不易解決的問題轉(zhuǎn)化為有章可循、容易解決的問題的思想.

（作者單位：江蘇省常州市金壇區(qū)直溪中學(xué)）