學科教學知識視角下的《導數的應用》復習課教學
北京市懷柔區第一中學 李 悅 張燕勤 符谷雨
一、問題的提出
學科教學知識(Pedagogical Content Knowledge)首先由舒爾曼在1986年提出,簡稱PCK,他認為PCK是教師在面對具體的學科時,如何針對不同學生的不同興趣以及能力,將學科知識進行合理組織、有效調整與充分呈現,從而達到有效的教學目的的知識。這種知識既是一種區分教師與學科專家的專門知識,也是一種可教性的學科知識[],屬于學科知識中的一種具體有效的形式。
二、教學設計總體思路
揭示函數單調性質的關鍵是導函數符號的確定或是直接利用導函數的零點進行判斷,而導函數的符號又與導函數的零點密切相關。本節課是一節高三第二輪的復習課,學生已經掌握了用導數研究函數單調性的基本方法,也積累了這類問題的解題經驗。在研究過程的各個階段中存在的問題有:求導函數出現錯誤、不能判斷導函數的函數值情況、不能處理導函數有零點但不可解的情況等。為此,我們從導函數無零點、導函數有零點且可解、導函數有零點但不可解三個方面分別選取組織例題,對導函數零點的不同情形的處理辦法做了分析梳理。根據學科知識內容和學生的掌握情況,我們選擇和組織了以下內容材料,用于兩課時的課堂教學。
例1,判斷下列函數的單調性
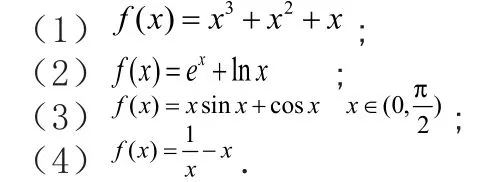
例2,判斷函數的單調性
變式:設a為實數,求證:當且x>0時
例4,證明函數:存在最小值.
上述內容安排了兩課時的教學時間,梳理導數應用的相關知識,讓學生在分析解決較為復雜函數的問題中,進一步認識和體會導數用于研究函數單調性的本質內容和重要作用。第一課時是針對導函數無零點的問題展開教學討論,第二課時是針對導函數有零點的問題展開教學討論。下文我們從學科教學知識的視角進行課堂觀察與分析,限于篇幅,這里僅介紹第一課時的教學過程,以實錄的形式呈現。
三、課堂教學片段:不能直接判斷導函數符號的樣例的討論
師:來看 例2。我找一位同學上來做。(學生做題,教師巡視)
師:好,我們來看一看生8做的情況。
原函數定義域為R,求出的導函數有問題嗎?
生眾:沒有。
師:然后生8畫了個圖。生8你來解釋一下你是怎么想的。
生8:就是要看導函數符號,我把它分成兩個,一個是ex和x…
師:為什么要分成兩個?
生8:因為我發現單從導函數,看不出來它的正負。
師:那你有沒有解方程找零點呢?
生8:我解不出來。
師:為什么解不出來?
生8:因為求值不好使了。
師:實際上是因為它們是兩個不同類型的函數,目前我們還解決不了,所以你想到了什么?
生8:畫圖。
師:好,因為它(指)解不了所以畫圖。那你畫圖的目的是把它轉化為什么問題?
生8:圖象問題。
師:圖象。是想看什么呢?
生8:交點、正負。
師:看它有沒有交點,判斷一下正負。好,大家看這個圖象,看他畫的對不對?
生9:我沒畫圖象。
師:好,讓他說完你再說,行嗎?這圖像大家說他畫的對不對?
師生眾:對。
師:實際上我們可以把圖象畫的標準點,指數函數過(0,1),還過(1,e);而正比例函數過的是(1,1)。我們這邊(指x軸負半平面)還有什么?和(-1,-1)。我們還可以找到(2,e2)。顯然它(指函數ex的圖像)在它(指函數x的圖象)的上方。之后這個函數我們可以觀察到它增長非常的快,我們管他叫什么函數?
師生眾:爆炸函數。
師:對,它增長得非常的快。而正比例函數是一直這樣勻速增長,所以它們的圖象應該是ex始終在y=x的上方,對嗎?
生8:對。
師:很好,請坐。有不同意見嗎?生9你說說。
生9:圖象不能用于證明。
師:圖象不能用于“由圖可知”這。好,非常不錯。“圖象不能用于嚴格證明”,大家同意嗎?
眾生:同意。
師:對,圖象只是我們的一個輔助工具。有的圖象,當然我們能看到它們之間的關系;而有的圖象,可能會導致你看似可能沒有交點,但實際上是有交點的,對吧?因此,它只能作為一種輔助的工具直觀感受。那么我們要想說理就需要用代數來證明,就所謂的“算”。好,生9請繼續。
生9:說明
師:同意嗎?
眾生:同意。
師:好,這是我們的目標。現在怎么把這事說清楚了?
生眾:再求一遍、再導一遍……
師:把它看做新函數再導一遍。再導的目的是什么?
生眾:求它的最值。
師:我們的目標是證明對吧?所以我們再導一遍目標是要說明
師生眾:最小值大于零。
師:同意嗎?
生眾:同意。
師:好。接下來我們來把它完善。(選生10上黑板完成)
四、案例分析
課程標準對導數與函數的單調性的要求是,結合實例,借助幾何直觀探索并了解函數的單調性與導數的關系,能利用導數研究函數的單調性;教師應引導學生在解決具體問題的過程中,將研究函數的導數的方法與初等方法做比較,以體會導數方法在研究函數性質中中的一般性和有效性。我們認為,雖然是一個復習課內容,但是作為導數與函數單調性這一特定課題的一部分,突出其最有教學價值的知識,即其中的數學思想和思維價值,仍應是教學目標的最基本定位。
片段1中,安排了復習回顧利用導數研究函數單調性的基本步驟,并且引導學生對導函數零點的的不同情況提出有零點和無零點的簡單分類。讓學生通過解決問題來強化利用導數解決函數單調性問題的方式與方法。通過總結研究的一般步驟,為解決函數單調性問題提供了定向。例1選擇四個函數作為判斷單調性的任務,它們覆蓋了初高中學習過的冪函數、指數函數、對數函數、三角函數,對適當組合之后得到的這四個函數的求導任務,需要用到上述函數的導數公式和求導法則;要判斷所求導函數的符號,需要對導函數解析式進行適當的變形(如配方),特別需要注意函數的定義域。從一些簡單函數的練習入手,讓學生在整個教學過程中始終都能夠體會到導數研究函數的工具性作用。關于例2,學生很容易求出它的導函數,但是既不能直接判斷導函數的符號,也不會求其導函數的零點。
上述內容的選擇和布局,是導數的應用這一特定課題的需要,能夠體現相關的概念體系和邏輯脈絡,兼顧了導數的基礎知識、研究函數性質的基本技能、以及數形結合、分類討論等數學思想方法。

