幾例易錯的數形結合題
山東省寧陽一中 (271400) 朱存東
幾例易錯的數形結合題
山東省寧陽一中 (271400) 朱存東
數形結合作為一種數學思想方法,其應用大致可分為兩種情形:或者借助于數的精確性來闡明形的某些屬性,即“以數解形”;或者借助形的幾何直觀性來闡明數之間的某種關系,即“以形助數”.有時候,我們在借助形來解決數的問題的時候,若圖形畫得不夠準確,這不但不會幫助解題,反而會弄巧成拙,事與愿違.下面列舉幾例易錯的數形結合題目,供參考.
例1 函數y=x2的圖像與y=2x的圖像的交點有 個.
錯解:畫出y=x2的圖像與y=2x的圖像如圖1,可知有兩個交點.
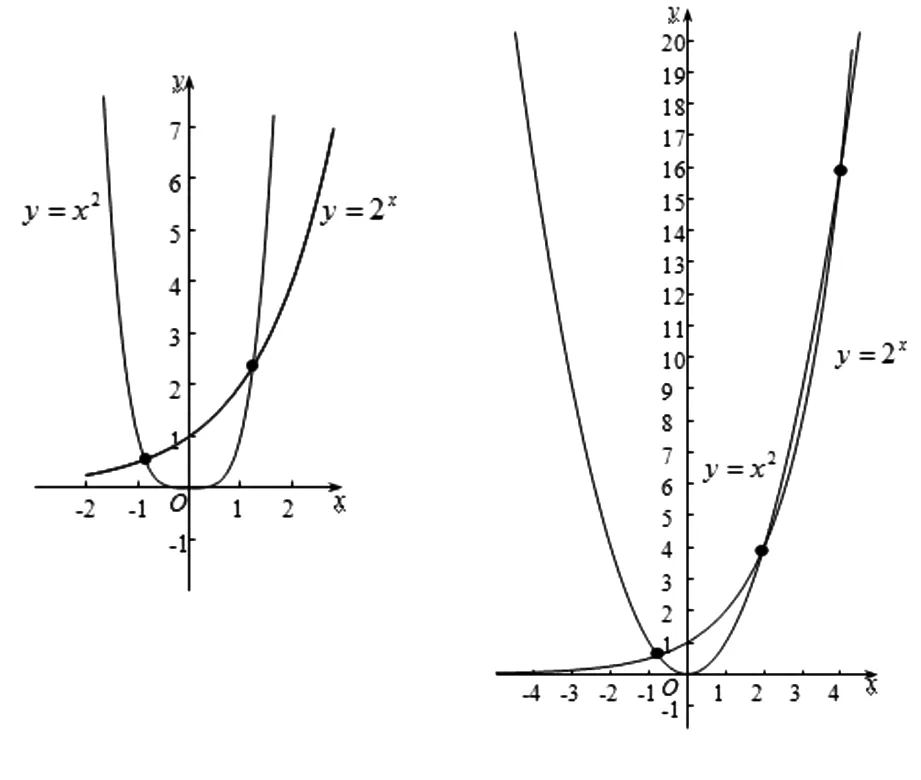
圖1 圖2
正解:因為x>1指數型函數的增長速度比冪函數的增長速度快,所以,當自變量x比較大時,y=2x的圖像要在y=x2的圖像的上方.由圖像可知,x<0時,y=2x的圖像與y=x2的圖像必有一交點,x>0時,設f(x)=x2-2x,因為f(1)-1-2=-1<0,f(3)=9-8=1>0,f(5)=16-25=-9<0,所以存在零點x1∈(1,3),x2∈(3,5),如圖2,經計算知,兩零點分別為2,4,即交點為(2,4)(4,16).
故兩函數共有3個交點.
例2 求正弦曲線y=sinx的圖像與直線y=x的交點個數.
錯解:畫出y=sinx與y=x的圖像如圖3,可知y=sinx的圖像與y=x的圖像有三個交點.
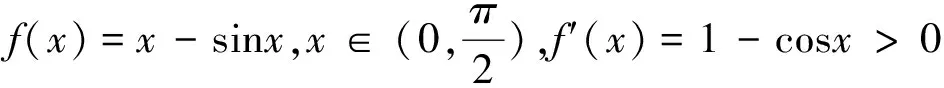
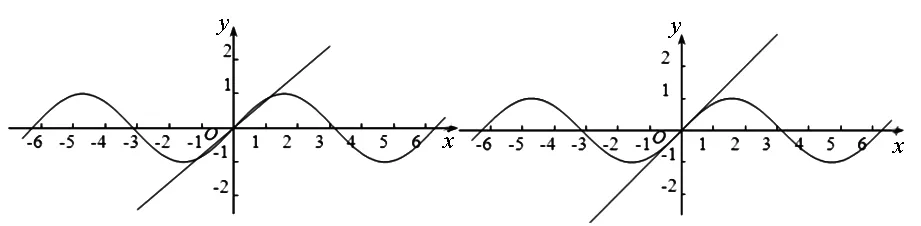
圖3 圖4
例3 方程ex=x+1解的個數有 個.
錯解:方程ex=x+1解的個數,即求y=ex圖像與y=x+1圖像交點的個數,畫出y=ex的圖像與y=x+1的圖像如圖5,顯然有兩個交點.
正解:方程ex=x+1解的個數即求y=ex圖像與y=x+1圖像交點的個數,因為兩個圖像均經過點(0,1),不妨先求一下經過y=ex圖像上一點(0,1)處的切線.
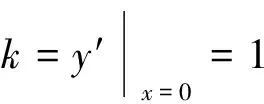
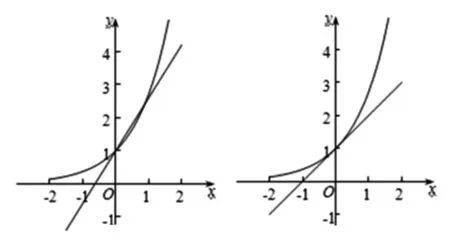
圖5 圖6
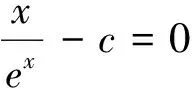
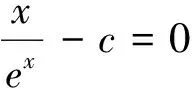
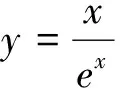
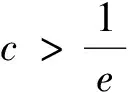
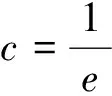
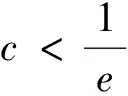
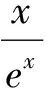
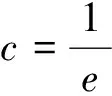
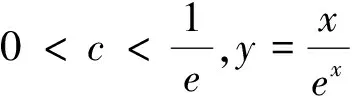

圖7 圖8
——山東省濟寧市老年大學之歌

