頻域兩尺度下一類Filippov系統(tǒng)的非光滑分析

楊秀芳，張正娣，李紹龍，畢勤勝

頻域兩尺度下一類Filippov系統(tǒng)的非光滑分析

楊秀芳，張正娣，李紹龍，畢勤勝

(江蘇大學(xué)理學(xué)院，江蘇鎮(zhèn)江212013)

借助于含非光滑分界面的耦合Bohoffer-Van der Pol(BVP)電路系統(tǒng)，引入周期慢變的交流電源，構(gòu)建兩頻域尺度的Filippov系統(tǒng)。利用微分包含理論，分析了尺度因素與非光滑因素相互作用的機(jī)理。當(dāng)周期激勵(lì)頻率遠(yuǎn)遠(yuǎn)小于系統(tǒng)固有頻率時(shí)，選取適當(dāng)參數(shù)，得到了具有滑動(dòng)結(jié)構(gòu)的復(fù)雜周期簇發(fā)振蕩，并結(jié)合理論分析揭示了滑動(dòng)結(jié)構(gòu)的產(chǎn)生機(jī)制。數(shù)值結(jié)果與理論分析吻合較好。

Filippov系統(tǒng);頻域兩尺度;非光滑;簇發(fā);滑動(dòng)結(jié)構(gòu)

0 引言

非光滑動(dòng)力系統(tǒng)的研究，越來越引起國(guó)內(nèi)外學(xué)者的興趣和關(guān)注。Filippov系統(tǒng)作為一類典型的非光滑動(dòng)力系統(tǒng)，反映到數(shù)學(xué)模型上，可以表示為右端不連續(xù)的常微分方程(組)，諸多學(xué)科領(lǐng)域內(nèi)的非光滑問題，都可以用此類模型來描述。例如，干摩擦系統(tǒng)［1］、切換電路［2］、生態(tài)與經(jīng)濟(jì)動(dòng)力學(xué)的閾值［3－4］、電機(jī)中的間隙［5］、生物種群的庇護(hù)行為［6］和疾病動(dòng)力學(xué)中的媒介效應(yīng)［7］等。

至今，對(duì)Filippov系統(tǒng)動(dòng)力學(xué)行為的研究已取得諸多成果，如文獻(xiàn)［8］給出了干摩擦系統(tǒng)分岔與混沌的實(shí)驗(yàn)結(jié)果。分段線性系統(tǒng)作為一類特殊的Filippov系統(tǒng)，文獻(xiàn)［9］研究了參數(shù)激勵(lì)下分段線性兩尺度系統(tǒng)的分岔。文獻(xiàn)［10］通過施加連續(xù)和匹配條件考慮了分段弱非線性振子在周期激勵(lì)下的對(duì)稱型周期運(yùn)動(dòng)。文獻(xiàn)［11］拓展了文獻(xiàn)［12］的研究?jī)?nèi)容，通過尤金等價(jià)的思想，利用非光滑分界面相對(duì)于兩側(cè)光滑向量場(chǎng)的方向?qū)?shù)，在理論上給出了滑動(dòng)分岔以及擦邊分岔的規(guī)范型。文獻(xiàn)［13］基于Floquet乘子理論，通過引入輔助參數(shù)q，分析了激勵(lì)下的黏滑系統(tǒng)中穩(wěn)定周期軌道與不穩(wěn)定周期軌道在非光滑分界面處的動(dòng)力學(xué)行為，指出了周期軌道Floquet乘子跳躍式的穿出單位圓的不連續(xù)分岔。但上述研究都是在單一尺度上，并沒有考慮廣泛存在的尺度因素對(duì)這一類典型非光滑系統(tǒng)的動(dòng)力學(xué)行為的影響。

基于此，本文借助一個(gè)拓展的具有閾值控制特性的耦合廣義Bohoffer-Van der Pol(BVP)電路系統(tǒng)［14］，引入一個(gè)慢變交流電源，構(gòu)建一個(gè)兩頻域尺度的Filippov系統(tǒng)，其無量綱動(dòng)力學(xué)方程表示為:

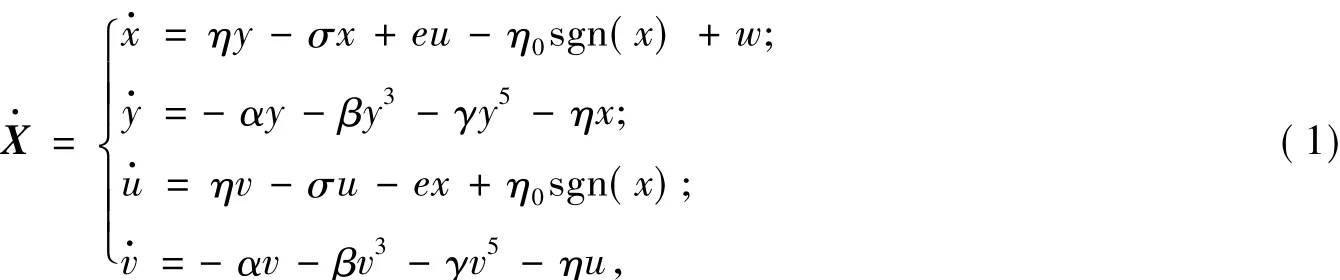
其中:向量X=［xyuv］T;x，y，u，v為狀態(tài)變量;α，β，γ，σ，η，e，η0為參數(shù)。系統(tǒng)(1)中周期激勵(lì)項(xiàng)w=10Usin(Ωτ)，U和Ω分別為外激勵(lì)振幅和頻率，τ為無量綱時(shí)間。

首先通過微分包含理論，探討尺度因素與非光滑因素之間的相互作用機(jī)制，并分析系統(tǒng)(1)在分界面可能出現(xiàn)的動(dòng)力學(xué)行為;然后，選取適當(dāng)參數(shù)，得到了典型的周期簇發(fā)振蕩，并結(jié)合數(shù)值結(jié)果驗(yàn)證了理論分析的正確性。

1 非常規(guī)分岔分析

由于系統(tǒng)(1)的向量場(chǎng)不連續(xù)，為典型的Filippov系統(tǒng)，借助于微分包含理論，引入輔助參數(shù)q∈［0，1］，討論系統(tǒng)軌線在與非光滑分界面Σx=0接觸時(shí)的動(dòng)力學(xué)行為，系統(tǒng)(1)可進(jìn)一步改寫為:

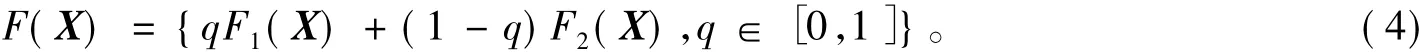
為了明確尺度因素與非光滑因素之間的相互作用關(guān)系，在非光滑分界面Σx=0上，定義系統(tǒng)(1)滿足x·=0的區(qū)域，形式如下:

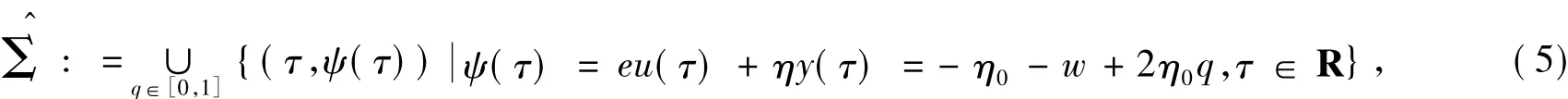
其中:ψ(τ)為eu(τ)+ηy(τ)或－η0－w+2η0q;q為連續(xù)閉集。對(duì)于任意時(shí)刻τ=τ'，假定η0＞0，則集存在上確界與下確界，分別為:

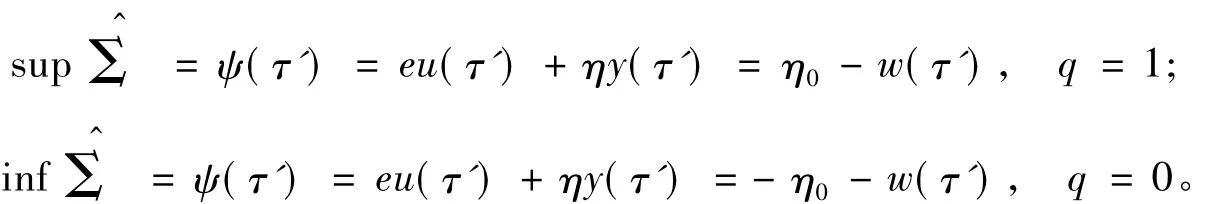
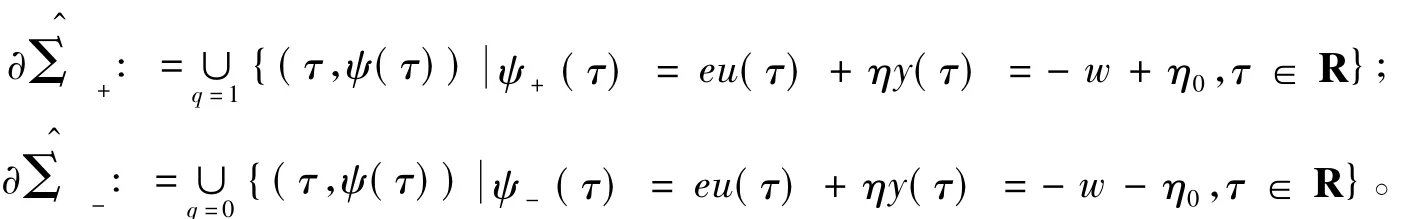
圖1為分界面處·x在單個(gè)激勵(lì)周期下的示意圖。如圖1所示，邊界可以將的取值范圍在分界面處劃分為4個(gè)部分:位于邊界以上的區(qū)域Ⅰ、位于邊界以下的區(qū)域Ⅲ、邊界所圍成的區(qū)域以及邊界本身。不妨假設(shè)在時(shí)刻τ'，軌線從任意光滑區(qū)域到達(dá)非光滑分界面顯然滿足x(τ')=0。下面，根據(jù)·x的取值情況，繼續(xù)討論軌線在非光滑分界面處的動(dòng)力學(xué)行為。

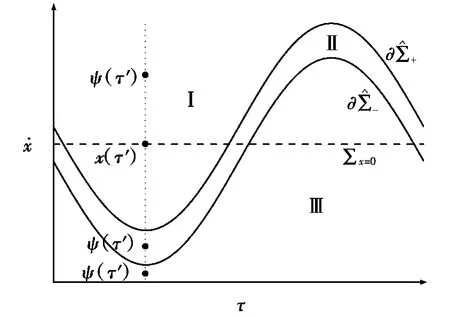
圖1 分界面處x·在單個(gè)激勵(lì)周期下的示意圖

首先，根據(jù)x(τ')=0時(shí)對(duì)應(yīng)的曲線ψ(τ')在圖1所處的位置，得到3個(gè)確定區(qū)域，即軌線將在下一時(shí)刻的動(dòng)力學(xué)行為是明確的。當(dāng)ψ(τ')位于區(qū)域Ⅰ:x·＞0，則系統(tǒng)軌線由區(qū)域D－到達(dá)，并將橫截穿過非光滑分界面后進(jìn)入?yún)^(qū)域D+運(yùn)動(dòng)。當(dāng)ψ(τ')位于區(qū)域，滿足x·(τ')=ψ(τ')+ w(τ')－2q'η0+η0=0，其中，q'∈(0，1)滿足多值條件，且由于系統(tǒng)狀態(tài)變量是連續(xù)的，則系統(tǒng)軌線將在接下來的一段時(shí)間駐留在當(dāng)ψ(τ')位于區(qū)域Ⅲ:x·(τ')＜0，則系統(tǒng)軌線是由區(qū)域D+到達(dá)，并將橫截穿過非光滑分界面后進(jìn)入?yún)^(qū)域D－運(yùn)動(dòng)。將區(qū)域Ⅰ與區(qū)域Ⅲ稱為橫截穿過區(qū)域，將區(qū)域Ⅱ稱為系統(tǒng)的滑動(dòng)區(qū)域。

2 數(shù)值驗(yàn)證

選取參數(shù)σ=－0.2，η0=4.0，η=2.2，β=－0.8，γ=3.0，α=0.21，e=2.2，Ω=0.01，由于激勵(lì)頻率和系統(tǒng)固有頻率之間存在量級(jí)上的差異，系統(tǒng)往往會(huì)表現(xiàn)出快慢耦合的動(dòng)力學(xué)行為，即簇發(fā)振蕩。當(dāng)U=10.0時(shí)，系統(tǒng)的軌線與非光滑分界面Σx=0接觸，并呈現(xiàn)出一個(gè)自身關(guān)于原點(diǎn)對(duì)稱的周期簇發(fā)振蕩，如圖2所示。

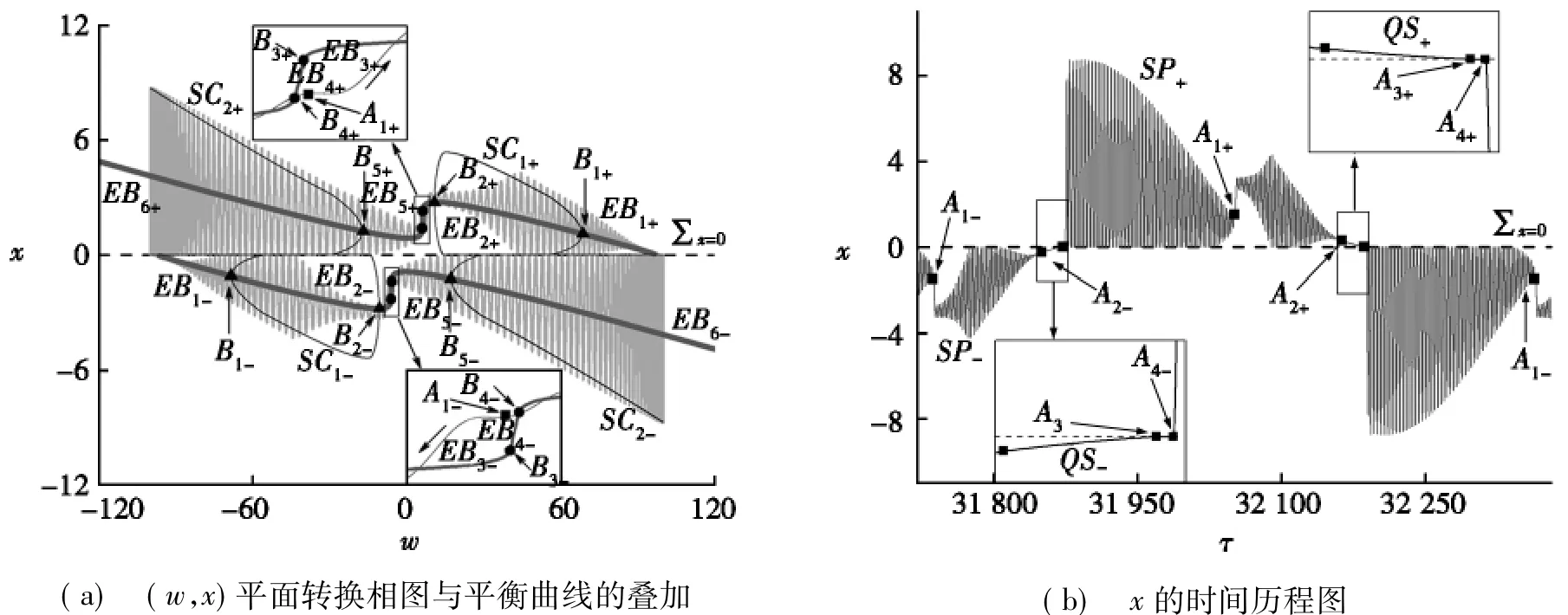
圖2 系統(tǒng)(1)在U=10.0時(shí)的周期簇發(fā)振蕩

圖2a給出了系統(tǒng)U=10.0時(shí)，在(w，x)平面逆時(shí)針運(yùn)動(dòng)的周期簇發(fā)振蕩的轉(zhuǎn)換相圖及其與系統(tǒng)平衡曲線的疊加圖，圖2b為對(duì)應(yīng)的狀態(tài)變量x的時(shí)間歷程圖。數(shù)值結(jié)果顯示:整個(gè)周期簇發(fā)振蕩包含了兩個(gè)激發(fā)態(tài)SP±和兩個(gè)沉寂態(tài)QS±，如圖2b所示。通過對(duì)系統(tǒng)常規(guī)分岔的計(jì)算可以發(fā)現(xiàn):由超臨界Hopf分岔B1±、B2±和B5±(如圖2a中的三角形所示)生成的穩(wěn)定極限環(huán)SC1±與SC2±(如圖2a中細(xì)實(shí)線所示)，導(dǎo)致軌線圍繞平衡線(如圖2a中粗實(shí)線所示)振蕩(激發(fā)態(tài))，而這里的亞臨界Hopf分岔B3±與B4±使得平衡線的穩(wěn)定性發(fā)生改變，加上平衡線此時(shí)上下方向存在一定距離，導(dǎo)致軌線出現(xiàn)跳躍現(xiàn)象，處于激發(fā)態(tài)。軌線在越過分岔點(diǎn)B1±后，逐漸收斂到平衡線上并沿著平衡線運(yùn)行(沉寂態(tài))。

結(jié)合上述對(duì)于系統(tǒng)軌線接觸非光滑分界面時(shí)可能出現(xiàn)的動(dòng)力學(xué)行為的分析，揭示整個(gè)周期簇發(fā)振蕩中出現(xiàn)的兩種不同滑動(dòng)結(jié)構(gòu)的形成機(jī)制。圖3給出了一個(gè)振蕩周期內(nèi)的時(shí)間歷程、滑動(dòng)邊界與曲線ψ(τ)的疊加圖。

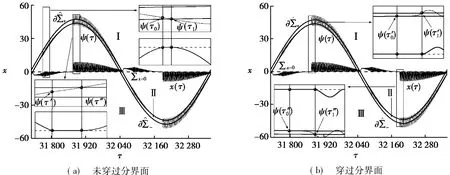
圖3 時(shí)間歷程、滑動(dòng)邊界與ψ(τ)的疊加

首先，結(jié)合數(shù)值結(jié)果來討論位于激發(fā)態(tài)中的“從分界面一側(cè)進(jìn)入分界面-滑動(dòng)-返回分界面同一側(cè)”滑動(dòng)結(jié)構(gòu)的成因。假設(shè)以位于激發(fā)態(tài)SP－的點(diǎn)A1－為整個(gè)周期簇發(fā)振蕩的起始點(diǎn)，隨著軌線的運(yùn)行，如圖3a右上角的局部放大圖所示，在τ0時(shí)刻，軌線首次由光滑區(qū)域D－到達(dá)分界面，對(duì)應(yīng)時(shí)刻的曲線ψ(τ0)在此時(shí)落在滑動(dòng)區(qū)域內(nèi)部，由于系統(tǒng)變量的連續(xù)性，軌線將在分界面內(nèi)運(yùn)行一段時(shí)間，出現(xiàn)滑動(dòng)現(xiàn)象。而在時(shí)刻τ1，曲線ψ(τ)與滑動(dòng)邊界橫截相交，并在此后進(jìn)入橫截區(qū)域Ⅲ，導(dǎo)致軌線隨后脫離分界面并返回光滑區(qū)域D－。由數(shù)值結(jié)果可以發(fā)現(xiàn)，軌線在激發(fā)態(tài)SP－中多次呈現(xiàn)出從區(qū)域D－進(jìn)入分界面-滑動(dòng)-返回區(qū)域D－的滑動(dòng)振蕩模式，其成因與軌線在時(shí)間區(qū)間［τ0，τ1］相同。相應(yīng)地，軌線在激發(fā)態(tài)SP+中多次出現(xiàn)從區(qū)域D+進(jìn)入分界面-滑動(dòng)-返回區(qū)域D+的滑動(dòng)振蕩模式，其原因可相似地分析。

可見，軌線在整個(gè)周期簇發(fā)振蕩中出現(xiàn)的兩種滑動(dòng)結(jié)構(gòu):“從分界面一側(cè)進(jìn)入分界面-滑動(dòng)-返回分界面同一側(cè)”與“進(jìn)入分界面-滑動(dòng)-穿過分界面”，數(shù)值結(jié)果和本文的理論分析吻合較好。

3 結(jié)束語

對(duì)于周期外激勵(lì)下Filippov系統(tǒng)，當(dāng)外激勵(lì)頻率遠(yuǎn)遠(yuǎn)小于系統(tǒng)的固有頻率時(shí)，系統(tǒng)存在頻域兩尺度。把整個(gè)周期外激勵(lì)項(xiàng)看作一個(gè)慢變參數(shù)，利用微分包含理論，根據(jù)尺度因素與非光滑因素之間的相互作用機(jī)制，采取時(shí)間序列的分析法，分析了系統(tǒng)在非光滑分界面處可能出現(xiàn)的動(dòng)力學(xué)行為。在數(shù)值驗(yàn)證中，得到了系統(tǒng)具有滑動(dòng)結(jié)構(gòu)的復(fù)雜周期簇發(fā)振蕩，其滑動(dòng)結(jié)構(gòu)的產(chǎn)生與理論分析吻合較好。

［1］張有強(qiáng).干摩擦碰撞振動(dòng)系統(tǒng)的非線性動(dòng)力學(xué)研究［D］.蘭州:蘭州交通大學(xué)，2008.

［2］陳章耀，王亞茗.切換電路時(shí)間對(duì)非線性切換系統(tǒng)振蕩特性的影響［J］.河南科技大學(xué)學(xué)報(bào)(自然科學(xué)版)，2016，37(5):87－90.

［3］BERNARDO M D，VASCA F.Discrete-time maps for the analysis of bifurcations and chaos in DC/DC converters［J］.IEEE transactions on circuits＆systems-part I(fundamental theory＆applications)，2000，47(2):130－143.

［4］BOR Y J.Uncertain control of dynamic economic threshold in pest management［J］.Agricultural systems，2003，78(1): 105－118.

［5］ZHOU Z，TAN Y，XIE Y，et al.State estimation of a compound non-smooth sandwich system with backlash and dead zone［J］.Mechanical systems＆signal processing，2016，83:439－449.

［6］CHEN X，HUANG L.A Filippov system describing the effect of prey refuge use on a ratio-dependent predator-prey model［J］.Journal of mathematical analysis＆applications，2015，428(2):817－837.

［7］WANG A，XIAO Y A.Filippov system describing media effects on the spread of infectious diseases［J］.Nonlinear analysis hybrid systems，2014，11(1):84－97.

［8］CSERNK G，STPN G.On the periodic response of a harmonically excited dry friction oscillator［J］.Journal of sound＆vibration，2006，295:649－658.

［9］陸慧玲，李紹龍，張正娣.參數(shù)激勵(lì)下分段線性兩尺度系統(tǒng)的分岔［J］.河南科技大學(xué)學(xué)報(bào)(自然科學(xué)版)，2015，36(6):71－74.

［10］JI J C，HANSEN C H.Approximate solutions and chaotic motions of a piecewise nonlinear oscillator［J］.Chaos，solitons＆fractals，2004，20(5):1121－1133.

［11］COLOMBO A，BERNARDO M D，HOGAN S J，et al.Bifurcations of piecewise smooth flows:perspectives，methodologies and open problems［J］.Physica d(nonlinear phenomena)，2012，241(22):1845－1860.

［12］FEIGIN M I.The increasingly complex structure of the bifurcation tree of a piecewise-smooth system［J］.Journal of applied mathematics and mechanics，1995，59(6):853－863.

［13］LEINE R I，CAMPEN D H.Bifurcation phenomena in non-smooth dynamical systems［J］.European journal of mechanicsa (solids)，2006，25(4):595－616.

［14］WU X P，WANG L C.Codimension-2 bifurcations of coupled BVP oscillators with hard characteristics［J］.Applied mathematics＆computation，2013，219(10):5303－5320.

O29

A

1672－6871(2017)05－0065－05

10.15926/j.cnki.issn1672－6871.2017.05.014

國(guó)家自然科學(xué)基金項(xiàng)目(11472115，11472116)

楊秀芳(1990－)，女，江蘇南京人，碩士生;張正娣(1972－)，女，江蘇丹陽人，教授，博士，博士生導(dǎo)師，主要研究方向?yàn)榉蔷€性動(dòng)力學(xué).

2017－03－01