基于客戶滿意度的多目標貨物配裝問題研究

文/李小玲 吳愛萍

基于客戶滿意度的多目標貨物配裝問題研究

文/李小玲 吳愛萍

本文在傳統的貨物配裝模型的基礎上引入客戶滿意度因素，從貨物配裝引起的貨損率對客戶滿意度的影響角度建立以貨損成本最小化以及車輛載重和容積利用率最大化為目標的多目標貨物配裝優化模型。

貨損率；客戶滿意度；多目標；貨物配裝優化

引言

流通型配送中心主要是服務于商業企業的貨物配送，這種貨物配送往往屬于一對多的配送形式，即由一個配送中心將貨物配送個m個客戶。而貨物配裝是配送的一個必經且重要的環節，學術上屬于相當復雜約束條件的組合優化問題，屬于NP～hard問題[1]。

在進行貨物配裝的過程中不可避免地會出現由于包裝、裝卸搬運以及貨物放置位置不當造成實際的貨物損壞，貨物損壞的程度直接影響了客戶對于物流企業的客戶滿意度。縱觀國內外關于貨物配裝的模型，在貨物配裝的建模過程中，所考慮的約束條件比較少，大部分都只考慮貨物的體積和重量約束[2～4]。此外，可以發現關于貨物配裝的建模，都是從企業、車的角度設立目標函數，沒有從客戶的角度如從客戶滿意度這個目標出發建立模型。

本文即從貨物配裝引起的貨損率與客戶滿意度的背反效應這個角度，以最大化客戶滿意度的目標出發來研究多目標的、考慮客戶滿意度的多車多品種貨物配裝問題。

1.貨損率與客戶滿意度關系

貨物配裝這一過程中，貨物損壞主要是來自包括裝卸搬運不當導致貨物在裝載工具內堆碼方式不當造成貨物擠壓、刺穿、撞擊、顛簸、倒塌或顛覆。

很明顯，貨損率與客戶對物流企業的滿意度呈負相關，貨損率越高，客戶滿意度越低，貨損率越低，相應地，客戶滿意度就越高[7]。因此，本文用貨損率來衡量貨物配裝的客戶滿意度。客戶對收到的貨物完好程度在一個區間內是可以接受的，超過這個區間，客戶對物流企業的滿意度就會下降。將這個區間定義為貨物配裝貨損率窗，如圖1所示：Smax表示客戶能夠接受的最大貨損率。貨損率在在[0，Smax]這個區間內，則客戶對物流企業完全滿意，超出這個區間，客戶滿意度就為零[5]。

圖1 貨損率區間描述

2.模型構建

2.1 問題描述

基于客戶滿意度的多車多品種貨物配裝問題可以描述如下：有一物流配送中心，l為配送中心車輛的集合，k為車輛的編號，k=1，2，…，l；n為配送中心待裝貨物的數目，j為貨物的編號，j=1，2，…，n；m為配送中心客戶的集合，i為貨物編號，i=1，2，…，m。配送中心在一定的貨損成本條件下，滿足客戶需求以及配送中心車輛載重和體積利用率最高的貨物配裝方案。

2.2 目標設定

傳統的貨物配裝問題多以車輛的載重和容積使用率最高為目標，本文結合顧客滿意度與傳統的目標，同時考慮到顧客滿意度與貨損率的關系，可將基于客戶滿意度的多車多品種貨物配裝問題的目標設定為如下3個：（1）貨損成本最小化；（2）車輛載重利用率最大化；（3）車輛容積利用率最大化，其中以貨損成本最小化為主要目標。

2.3 客戶滿意度表示

前面已經提到了在貨物配裝問題中客戶滿意度與貨損率之間的關系，因此客戶滿意度的最大化可用貨損成本最小化來來進行定量表示。

當客戶的貨物受到損壞，但實際貨損率小于客戶能夠容忍的最大貨損率Smax時，企業根據單位賠償價格和貨物損失總量賠償客戶的相應損失，這是由于貨物配裝不當而支出的成本，本文稱之為貨損成本。而貨損總量取決于貨物總量和總的貨損率[6]。以ai表示客戶收到的貨物的貨損率，ps為每單位貨物的賠償價格；di為客戶i的需求量，那么客戶i由于貨物配裝造成的貨損成本為psdiaixijk，模型基本假設：

（1）客戶收到的貨物中損壞的部分是由于貨物配裝過程中裝卸搬運不當、貨物在車輛內部堆碼方式不當導致在運輸途中損壞；

（2）貨物不經過中轉，直接由配送中心送往最終客戶；

（3）由于貨物配裝造成的貨損率ai以及客戶所能容忍的最大貨損率Smax都是正態分布隨機變量。之所以這樣假設，是因為通過對以往客戶對貨損率要求和實際貨損率情況進行統計分析，可以得到關于貨損率的大量統計數據，再對這些數據進行合理地擬合，就得到了貨損率的分布形式。由于正態分布的適用條件為：變量受多個微小的，獨立的隨機因素影響，而每個因素都不具有壓倒一切的主導作用。貨損率具有這一特點，因此這類變量服從正態分布的假設是成立的[6]；

（4）每個客戶所需貨物不能分割；

（5）只裝載車輛有載重量和體積的上限，所配送的貨物形狀標準，排除由于農產品形狀各異而可能形成的空隙；

（6）不考慮裝入同一輛車車內的貨物之間的相互影響，即產品之間都可以混裝。

2.4 變量定義

gij：表示客戶i的第j件貨物的重量；

vij：表示客戶i的第j件貨物的體積；

xijk：為{0，1}變量，等于1則表示客戶i的第j件貨物由車輛k裝載；否則；

yk：為{0，1}變量，等于1則表示車輛k被用來裝載貨物；否則；

Gk：為車輛k的載重量；

Vk：為車輛k的容積；

hi：為客戶i給定的服務水平

2.5 模型建立

建立基于客戶滿意度的多車多品種貨物的數學模型如下：

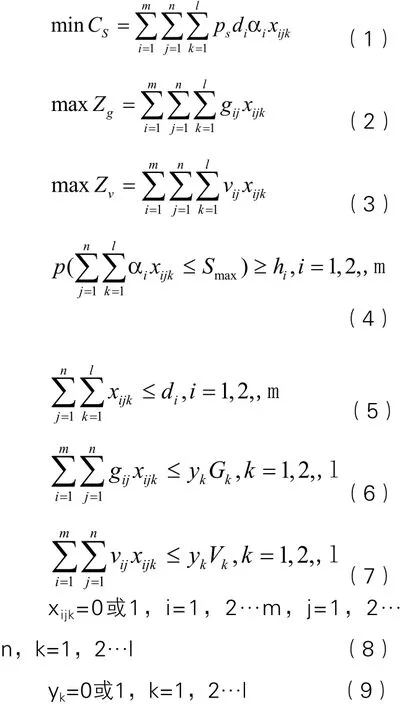
式中，式（1）～（3）中表示貨物配裝優化問題的目標；約束條件（4）表示客戶對貨損率限制的概率不小于給定的服務水平；約束條件（5）表示配送中心的貨物配送量不超過客戶的需求量；約束條件（6）表示每輛車裝載的貨物不超過車輛的載重量約束；式（7）表示每輛車裝載的貨物不超過車輛的容積約束；約束條件（8）表示每個客戶的貨物只裝一輛車的約束；約束條件（9）表示車輛被選中的約束。

2.6 算法實現

對于上述多目標貨物配裝問題的求解，可以參考R.Cheng和M.Gen在解決模糊VRP問題的混合遺傳算法來實現。這個方法使用push～bump～throw過程來處理問題模糊特征的插入啟發式操作可以有效地求解與之類似的問題[7]。

3.結束語

本文從貨損率與客戶滿意度背反這一點出發，以貨損成本最小來代替客戶滿意度最大化目標，在此基礎上建立基于客戶滿意度的貨物配裝優化模型，希望對貨物配裝問題的研究能夠起到一定的推動作用。但本文還存在一些不足之處，由于個人能力的有限，還沒找到一個很好的算法來實現這個模型的求解，是文章下一步需要仔細探討的方向。

[1]曹明蘭．配送中心貨物優化配裝問題的模型與算法研究[D]．武漢理工大學，2009：6～8．

[2]胡貴彥等．貨物配載方法最優化研究[J]．物流技術，2009，28（8）：86～89．

[3]謝天保．物流配送中心配載車輛調度問題研究[J]．計算機工程與應用，2010，46（36）：237～240．

[4]李江萍，但斌，陳軍．基于貨損約束的配送系統優化模型[J]．工業工程，2006，9（6）：66～69．

[5]張建勇，郭耀煌，李軍．基于顧客滿意度的多目標模糊車輛優化調度問題研究[J]．鐵道學報，2003，25（2）．

[6]李江萍．基于貨損和時間約束的流通型配送中心配送作業管理研究[D]．重慶大學：23～25．

[7]Herrera F，Verdegay J． Genetic algorithms and soft computing[M]．Heidelberg：Physica～Verlag，1996．683～709．

廣東理工學院質量工程項目，物流管理專業人才培養模式創新實驗區，項目編號CXSY2016004

（

廣東理工學院經濟管理學院）