關于三角函數概念構建的思考

蘇鑒強

（廣州市白云行知職業技術學校，廣東 廣州 510507）

[摘 要] 首先，對三角函數進行簡單的介紹，為下文的概念構建打好基礎。再次，相比以往的教學模式，對三角函數概念的構建進行創新講解。最后，從整體角度對此創新教學方式進行評價。

[關 鍵 詞] 三角函數；概念；構建

[中圖分類號] G712 [文獻標志碼] A [文章編號] 2096-0603（2017）09-0084-01

新課程標準的實施使初中教育降低了對運算能力的要求，降低了內容的整體難度，以及對函數部分的難度，導致學生在中職的數學課程學習中變得更加吃力，尤其是對三角函數的概念理解以及在三角函數基礎上的等價變換運算。然而由于函數的概念是數學課程的核心，如果學生對三角函數的概念存在混淆，沒有清楚地認識到三角函數中的一些基本概念，例如角的概念、任意角的函數運算以及正弦、余弦等基礎概念，則會對以后數學課程的學習產生不利影響。基于此，課程教師應該針對特定的數學教材，采用科學高效的教學方式和方法，使學生從本質上理解概念，吃透概念，便于以后知識的靈活運用和更進一步的學習。

一、三角函數的基本概念

三角函數又稱為圓函數，是因為其通常運用單位圓的形式來表示各個函數。三角函數的定義一般包含這個角的兩個邊長度的比值，或者是單位圓上各種線段的長度比。其本質是任何一角的集合域和一個比值的集合域的變量之間的映射關系，通常情況下，三角函數是在直角坐標系上的單位圓中定義的，也有的是在直角三角形中定義的。三角函數中最基本的函數有六種：正弦函數、余弦函數、正切函數、余切函數、正割函數、余割函數。

二、三角函數概念的構建

在中學的數學教材中，有些概念可以和實際相結合，通過聯系使學生了解概念的本質或內涵。但是也有許多概念不能通過此種方法進行教學，只能通過特定的語言進行講解，由于缺乏基本的認識，導致學生對這些概念的內涵以及外延都比較模糊，不能理解其確切的含義。例如，三角函數的概念，其內容全是基于數學語言來描述的，學生如果直接理解起來就很困難。因此，針對這樣的概念界定，我們可以結合獨特的教學方式，通過制定相關的教學目標來教學。

1.通過結合單位圓來認識三角函數，了解三角函數的定義，進一步了解何為定義域以及函數值。

2.在三角函數的教學過程中，首先應該激發學生的學習興趣，使其自主提問問題。當發現學生對這一問題有探索欲和求知欲的時候，便可進一步實施教學任務。

3.當學生初步掌握了基本的概念和定義之后，再幫助學生鞏固概念，建立整體概念體系，進一步提高其自主分析和解決相關三角函數問題的能力。

當學生在構建新的知識體系時，現有的知識存儲對新知識體系的構建起著非常重要的作用，在面臨新的知識框架時，學生會根據以往的學習經驗對新的知識形成自己的認識和理解，此時，教師在教學時不應該讓學生摒棄自己的理解和認知，反而應該鼓勵學生合理地推理，從現存的知識中延伸出新的知識。例如，在三角函數概念的教學中，由于在初中的時候，學生已經對銳角三角函數有了一定的了解，掌握了基本的概念。因此，在中職函數學習中，學生可以利用自己己有的知識，重新構建知識體系。

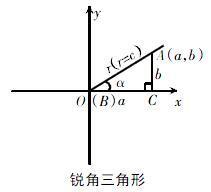
如圖所示，在直角三角形中，銳角α的正弦值=對邊長/斜邊長（b/r），余弦值=鄰邊長/斜邊長（a/r）。然而，在中職的課程中，角并不僅僅只限于銳角，而是任意角的問題。因此，此時銳角三角形就不能解決更深的問題，就需要把角放到直角坐標系中，放大角的范圍。在直角坐標系的單位圓中，進行任意角的界定，定義任意角的三角函數。

通過單位圓，在界定三角函數的概念時，三角函數可以看成以角的弧度數作為自變量，進行求解。也可以把角的度數作為自變量，以單位圓上定點的坐標比值來求得函數值。此外，教師在教學中，可以通過實際的例子來引進三角函數的概念以及后續的函數值計算。例如，2016年，我國在甘肅酒泉衛星發射中心成功發射了我國自主研制的神舟11號載人飛船，飛船進入太空后，在離地面較高的圓形軌道上圍繞地球做逆時針方向的勻速圓周運動，那么，如何確定變軌以后飛船在某一點的位置，圍繞地球飛行的飛船與地球之間的角與距離有怎樣的關系？飛船飛行的軌道可以看成是一個單位圓，將三角函數和實際案例結合起來，進一步講解三角函數的概念，學生理解起來更加清晰，便于理解。通過這樣的教學方式，可以加深學生對三角函數的理解，認清三角函數的本質。

相比之下，傳統的教學模式中教師只是在黑板上將各種三角函數的知識強加給學生，并沒有從本質上理解三角函數的概念，這就導致在以后的學習中，稍微變換一下形式，學生就不明白怎樣往下進行，不能活學活用。

三、結語

由于三角函數在數學中占據著很大的分量，對三角函數的概念掌握得好壞直接關系到后續的知識是否可以順利地學習下去。因此，對三角函數概念的構建，需要教師從根本上重視起來。將原本難以理解的三角函數變得容易讓學生接納，讓學生通過了解其本質和原理，對三角函數有一個深刻的認識和掌握。

參考文獻：

[1]李業霞.高中數學三角函數教學研究[D].內蒙古師范大學，2015.

[2]王永鋒.從“建構性學習”到“學生有效參與”[D].東北師范大學，2009.

[3]杜勝雪.建構主義與高中函數教學[D].河北師范大學，2008.