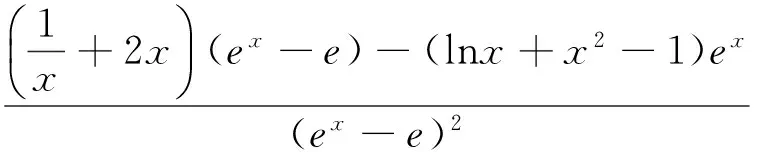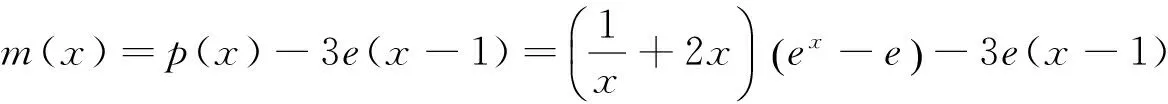對一道高三診斷試題的再探

四川省南充高級中學 (637000)

張小丹

對一道高三診斷試題的再探

四川省南充高級中學 (637000)

張小丹

題目 (2016綿陽一診21題)已知函數f(x)=lnx+ax2-1,g(x)=ex-e.

(1)討論f(x)的單調區間；

(2)若a=1，且對于任意x∈(1,+∞),mg(x)>f(x)恒成立，求實數m的取值范圍.

本題是2016年綿陽一診數學試卷(文理)第21題，第一題分類討論的思路并不復雜，大多學生能自行完成.對于第二題，從題干來分析，也是屬于常規題，不等式的恒成立問題，這考察的是導數在研究函數性質方面的一個應用：證明不等式或比較大小.咋一看，對于這類型的題目，學生在平時的練習過程中常有遇見—求參數的取值范圍，我們通常是直接構造函數法或者是分離參數法.

我們先展示參考答案給出的解法

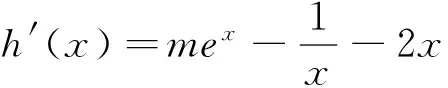
由q(x)=2x在[1，+∞)單調遞增，于是

q(x)min=2．∴p(x)min

若p(x)的圖像恒在q(x)的圖像的下方，此時p(x)

若p(x)的圖像與q(x)的圖像在x>1某點處相交，設第一個交點橫坐標為x0，當x∈(1，x0)時，p(x)

分析：參考答案是通過構造函數法，然后對參數m進行討論，從而得出m的取值范圍.

在研究這一試題的過程中，我試著用分離參數的方法來解決該題，如下

解法二：當x∈(1,+∞)時，mg(x)>f(x)

解法二雖然過程較繁，但是整個思路清晰，目標明確，步驟緊湊，沒有較生硬的學生難以理解的跳躍.另外，解法二也給我們提供了證明函數不等式的又一方法：

要證f(x)>g(x)，若一些直接的方法都不好處理的話，我們可以嘗試能否引進一條直線，l:y=kx+b，然后去證明f(x)>kx+b>g(x).當然這條直線l如何去找需要我們在解題的過程中多發現，多思考.