一道賽題的再思考
2017-08-28 11:17:05廣東省廣州市協和中學510160
中學數學研究(江西) 2017年8期
關鍵詞:數學
廣東省廣州市協和中學 (510160)
許云勇
一道賽題的再思考
廣東省廣州市協和中學 (510160)
許云勇
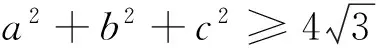
上述不等式也曾經作為第三屆國際中學生數學競賽試題,應該說它是數學中的一道經典不等式,對于該不等式,代數證明方法有多種,但基本上都是難以入手、計算量大,對學生的分析能力、計算能力都要求較高,筆者最近對該不等式作了一些探討,得到一種更為簡潔的幾何證法,同時得到與上述不等式相關的兩個新不等式鏈,現與讀者分享.
一、結論的幾何證明
證明:在ΔABC中不妨設a≥b≥c,如圖1,以BC為邊構造等邊ΔA′BC,記AA′=d,則∠ABA′=B
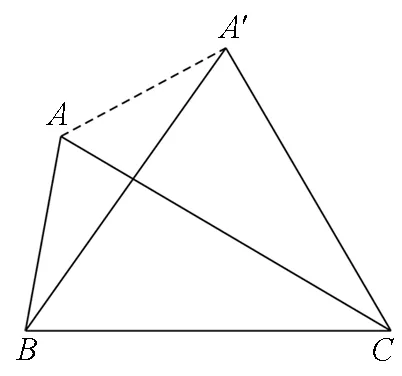
圖1
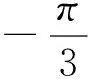
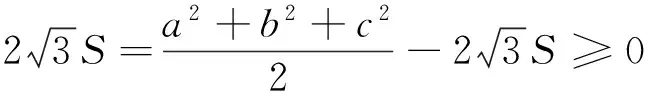
注:抓住不等式中等號成立的“關鍵”時刻,巧妙地通過分析一般時刻與關鍵時刻的異同,從而使得待證不等式通過幾何關系、代數運算得以體現!
二、相關的不等式鏈
事實上,對于不等式(1),我們可以得到一個更為完美的一個如下不等式鏈:
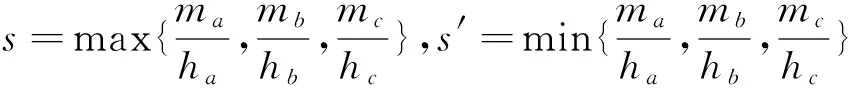
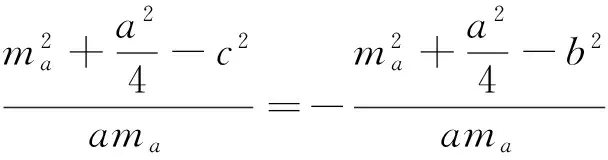
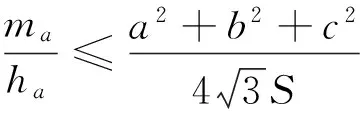
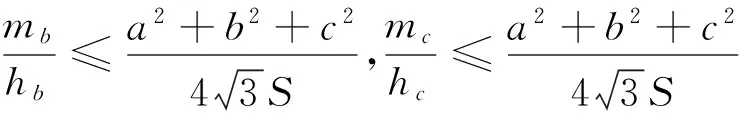
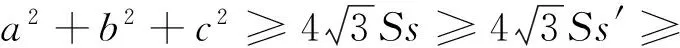
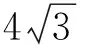
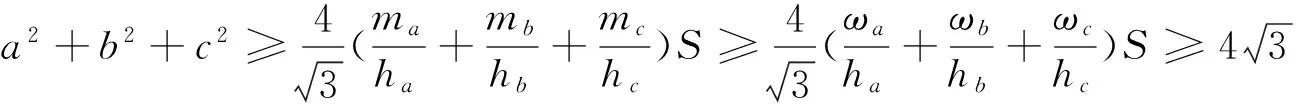
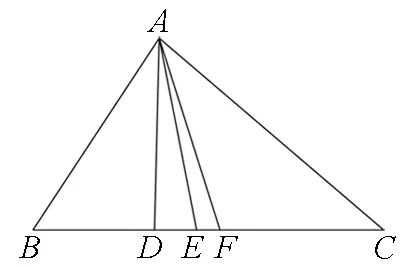
圖2
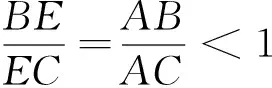
若AC=AB,不難看出ha=ωa=ma.故ha≤ωa≤ma,同理可得hb≤ωb≤mb,hc≤ωc≤mc.
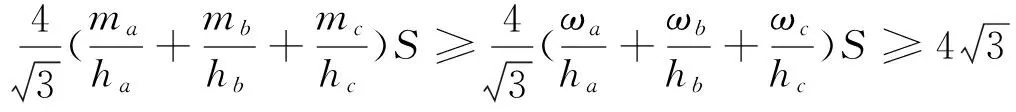
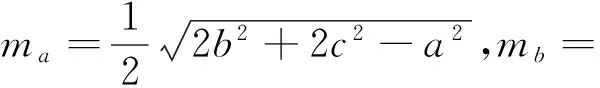
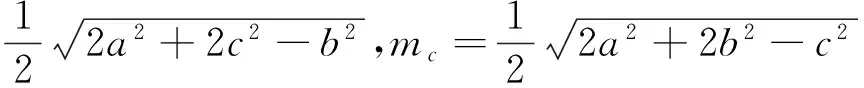
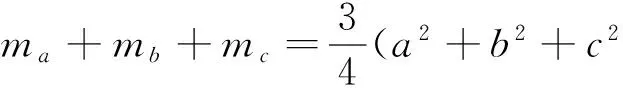
而由柯西不等式可知(a2+b2+c2)(ma+mb+mc)≥(ama+bmb+cmc)2,
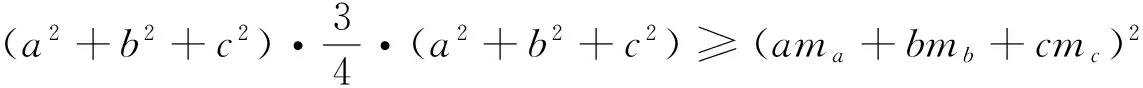

猜你喜歡
中等數學(2021年4期)2021-12-04 13:57:52
中等數學(2021年7期)2021-12-03 04:01:41
中等數學(2021年1期)2021-12-02 03:08:08
中等數學(2021年3期)2021-12-02 00:28:14
中等數學(2020年11期)2020-12-18 01:23:21
學苑創造·A版(2019年5期)2019-06-17 01:14:21
新民周刊(2016年15期)2016-04-19 18:12:04
新民周刊(2016年15期)2016-04-19 15:47:52
傳奇故事(破繭成蝶)(2015年7期)2015-02-28 09:29:27
漫畫月刊·炫版(2014年3期)2014-05-27 04:17:21

