對一道伊朗國家隊選拔考試題的推廣

廣州大學數學與信息科學學院 (510006)

邱際春

廣州大學附屬中學 (510006)

羅 芳

對一道伊朗國家隊選拔考試題的推廣

廣州大學數學與信息科學學院 (510006)

邱際春

廣州大學附屬中學 (510006)

羅 芳

2009年伊朗國家隊選拔考試第7題是一道組合幾何試題，如下：

題目 在平面內有三個由直線構成的集合，每個集合各由11條(不同的)平行線組成．若三組平行線內各存在一條直線通過平面內的同一點，求這樣的點的數目的最大值．[1]

首先，為了表述上的簡潔與方便，下面先給出一個定義：

定義 若平面內有m(m≥3)組平行線，且m組平行線內各存在一條直線通過平面內的同一點，稱這樣的點為m階特殊點．

接下來，將題目中的11條平行線推廣到n(n∈N*)條平行線的情形，得到下面的命題1．

解析:建立一個仿射標架[O;d1,d2]，則在仿射變換σ下，這三組平行線分別平行于x=0,y=0,y=x.

不妨設第一組平行線為x=i,i=1,2,…,n，記為x型直線；第二組平行線為y=j,j=1,2,…,n，記為y型直線；第三組平行線為x-y=b,b=1,2,…,n，記為x-y型直線．

根據定義，命題1中所述的點(即三條直線均通過的點)為3階特殊點．

接下來，考慮第一條x型直線(即x=1)和第一條y型直線(即y=1)，記P為兩直線的交點．

顯然，點P的左邊和下邊不存在3階特殊點．

容易看出，每一條x-y型直線與這兩條直線各交于一點，這些除點P之外的交點，要么在直線y=1上點P的左側，要么在直線x=1上的點P的下側．

因此，每一條x-y型直線至多通過一個第一條x型直線或第一條y型直線上的3階特殊點．

若擦去第一條x型直線和第一條y型直線，則至多移走了n個3階特殊點．

同樣地，每一條x-y型直線至多通過一個第二條x型直線或第二條y型直線上的3階特殊點．

再擦去第二條x型直線和第二條y型直線，則至多共移走了2n個3階特殊點．

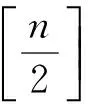
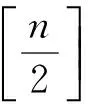
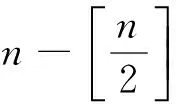
于是，對上述結論簡化，可得命題1的一個等價形式，表述為：

推論1 若平面內有三個由直線構成的集合，每個集合各由n(n∈N*)條(不同的)平行線組成，則①當n=2k時，平面內最多存在3k2個3階特殊點； ②當n=2k+1時，平面內最多存在3k2+3k+1個3階特殊點．

下面將命題1中的3個集合初步推廣到4個集合的情形可得命題2．

解析:建立一個仿射標架[O;d1,d2]，則在仿射變換σ下，這4組平行線分別平行于x=0,y=0,y=x,y=2x．

不妨設第一組平行線為x=i,i=1,2,…,n，記為x型直線；第二組平行線為y=j,j=1,2,…,n，記為y型直線；第三組平行線為x-y=b1,b1=1,2,…,n，記為x-y型直線；第四組平行線為2x-y=b2,b2=1,2,…,n，記為2x-y型直線．

根據定義，命題2中所述的點(即4條直線均通過的點)為4階特殊點．

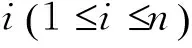
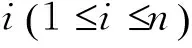
顯然，點P的左邊和下邊不存在4階特殊點．

容易看出，每一條2x-y型直線與這3條直線各交于一點，這些除點P之外的交點均在點P的左下方．

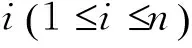
若擦去第一條x型直線、第一條y型直線和第一條x-y型直線，則至多移走了n個4階特殊點．

同樣地，再擦去第二條x型直線、第二條y型直線和第二條x-y型直線，則至多共移走了2n個4階特殊點．

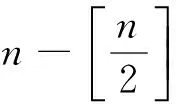
于是，問題轉化為：

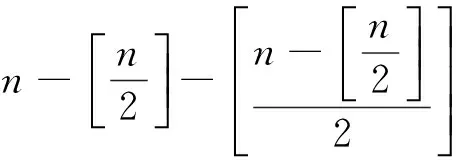
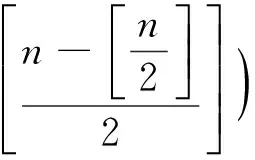
注意到，上述3階特殊點的個數唯一決定了4階特殊點的個數．

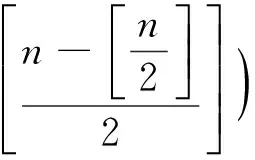
同樣地，簡化上述結論可得命題2的一個等價形式，表述為：

推論2 若平面內有4個由直線構成的集合，每個集合各由n(n∈N*)條(不同的)平行線組成，則①當n=22k-1或22k時，平面內最多存在3k2個3階特殊點； ②當n=22k+1或22k+2時，平面內最多存在3k2+3k+1個3階特殊點．

[1]2009年伊朗國家隊選拔考試[J]．中等數學，2010(增刊二)．