大豆期貨價格預測實證研究*

滕永平，周婷婷

（沈陽工業大學經濟學院，沈陽110870）

【經濟理論與應用】

大豆期貨價格預測實證研究*

滕永平，周婷婷

（沈陽工業大學經濟學院，沈陽110870）

在期貨市場中，無論是企業套期保值來規避風險，還是投資者進行投機來獲得利潤，對期貨價格進行合理預測都是特別重要的。選取2014－05－05—2015－08－31的大豆期貨合約數據，運用統計學及計量經濟學方法進行實證分析。利用ARMA模型進行預測，得出原數據與預測數據的對比圖，證明基于ARMA模型的短期價格預測機制具有一定的準確性，可以為投資者提供參考。

大豆；期貨價格；價格預測；ARMA模型；單位根檢驗；時間序列分析；白噪聲檢驗

隨著中國經濟的發展，期貨市場正在迅速崛起［1］，期貨交易逐步進入人們的經濟生活。雖然期貨市場存在一定風險性，但通過時間序列模型研究可以提供投資參考信息［2］。時間序列模型在不同的時刻有不同的信息，可以更為準確地預測期貨的價格走勢。時間序列是依賴于時間的一組時間變量，構成該時序的單個序列值雖然具有不確定性，但整個序列的變化具有一定的規律性，可以用相應的數學模型進行描述，再通過對數學模型的研究與分析實現最小方差下的最優預測。

一、國內外研究現狀

對期貨價格的預測一直是國內外研究的重點。國外期貨市場發展得較早，對期貨市場的研究更加深入。Volkan Ediger等用ARIMA模型對土耳其2005—2020年間主要的能源需求進行了預測，得出ARIMA模型對能源類非平穩時間序列數據有較好擬合和預測效果的結論［3］。有些國外學者運用神經網絡對價格進行預測，如Grudnitski G和Osburn L（1993）應用神經網絡對S＆P指數和黃金期貨價格進行預測［4］。Hossain等運用ARIMA模型對3種豆類的價格進行分析預測，通過相應對比分析發現這一模型對豆類價格具有較好的擬合和預測效果［5］。ARIMA模型與ARMA模型類似，只不過ARIMA模型中的I是對非平穩時間序列數據進行d次差分得到平穩數據后所建立的ARMA模型，差分次數d就是模型中的I值。

近年來，國內對期貨價格預測的研究也逐漸發展起來。國內對價格預測的主要方法集中于兩種：一是采用單一的模型進行檢驗與預測，二是運用兩種或兩種以上的模型進行比較或結合研究。楊嫻等利用模型分析國際有色金屬期貨的市場風險。何曉光等基于ARMA-GARCH模型與VAR模型，對上海同業拆借市場的利率風險進行研究［6］。梅志娟（2010）對ARMA模型和GARCH模型進行對比分析，得出GARCH模型預測銅期貨價格準確度更高的結論［7］。吳朝陽將ARMA模型與灰色模型結合起來對股指進行預測，并對灰色模型的缺陷進行改進，得出改進灰色模型和ARMA模型，使預測精度得到提高。閆冬（2012）基于ARMA-GARCH模型對上證指數進行短期的預測研究［8］。

本文采用大豆期貨2014－05－05—2015－08－31的真實交易數據，利用計量經濟學方法對ARMA模型進行實證分析，對大豆期貨價格的時間序列數據進行整理從而建立模型；根據所建立的數學模型對大豆期貨價格走勢進行預測，得出ARMA模型對大豆期貨價格的短期預測具有一定準確性的結論。總體來說，國外對ARMA模型的研究優于國內，但國內的研究數量也在逐步增加，有很大的發展潛力。

二、ARMA模型構建

ARMA模型由博克斯（Box）和詹金斯（Jenkins）創立，又稱B-J方法。該模型又稱自回歸滑動平均模型（auto-regressive and moving average model），是研究時間序列的重要方法，由自回歸模型（AR模型）與滑動平均模型（MA模型）為基礎“混合”構成。AR模型又稱自回歸模型（auto regressivemodel），是一種線性預測，即已知N個數據，可由模型推出第N點前面或后面的數據（設推出P點），其本質類似插值，目的是為了增加有效數據。AR模型是由N點遞推，而插值是由兩點（或少數幾點）去推導多點，所以AR模型要比插值方法效果更好［9］。MA模型即滑動平均模型（moving averagemodel），是模型參量法譜分析方法之一。ARMA模型的表達式為

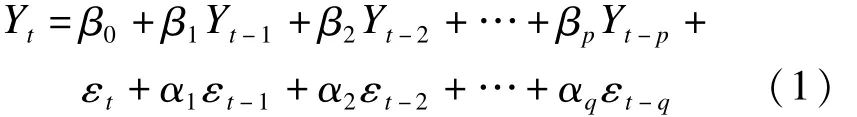
式中：p、q為模型的自回歸階數和移動平均階數；ai、βi為不為0的待定系數；Yt為平穩、正態、零均值的時間序列；εt為獨立誤差項。

ARMA模型構建共包含5個步驟：

第一步，平穩性檢驗。時間序列模型必須是平穩的才可以進行ARMA建模。對一個非平穩的時間序列模型，需要先對它進行d次差分處理，直到其變為平穩的時間序列模型。

第二步，模型識別。根據時間序列數據樣本自相關和偏自相關的值來確定模型中p和q的值，再根據最小信息準則來準確確定模型的階數。

第三步，模型的參數估計。利用最小二乘法對模型進行參數檢驗，使其在統計上顯著，具有統計意義。

第四步，模型的假設檢驗。模型選定之后對其進行白噪聲檢驗，若均落在指定區域，說明沒有需要再提取的信息。

第五步，預測。利用ARMA所建立的數學模型進行價格預測。

三、實證分析

1．數據選取

商品期貨通常情況下流通量大，參與者基本都是價格的接受者，接近于完全競爭市場，有利于利用數據預測價格。在期貨交易軟件上，時間分為月、周、日、分鐘。對選取數據而言，太短的周期具有突發性，不適合作為選取的對象；周期太長則會忽略掉中間的突變因素，同樣不適合作為選取的對象。因此，本文選取2014－05－05—2015－08－31豆一期貨的日收盤價作為研究數據。選擇每個合約交割月份前2個月的價格，如a1507是2015年7月到期的豆一合約，則選擇該合約交割前2個月即5、6月的合約，依此類推以便得到連續的期貨價格。對節假日及個別缺失的數據進行剔除，使得數據更加真實有效。共選取330個數據，其中前309個作為研究對象，后21個作為預測數據的對比對象，以檢測模型準確度。實證分析利用計量分析軟件Eviews 7.2完成。

2．ADF檢驗

為了避免偽回歸的產生，模型只有通過平穩性檢驗才有統計意義［10］。如果ADF檢驗中P＞0.05，則說明存在單位根，即數列具有不穩定性；若P＜0.05，則說明數據穩定［11］。原數列的單位根檢驗結果如表1所示，一階差分后的序列單位根檢驗結果如表2所示。

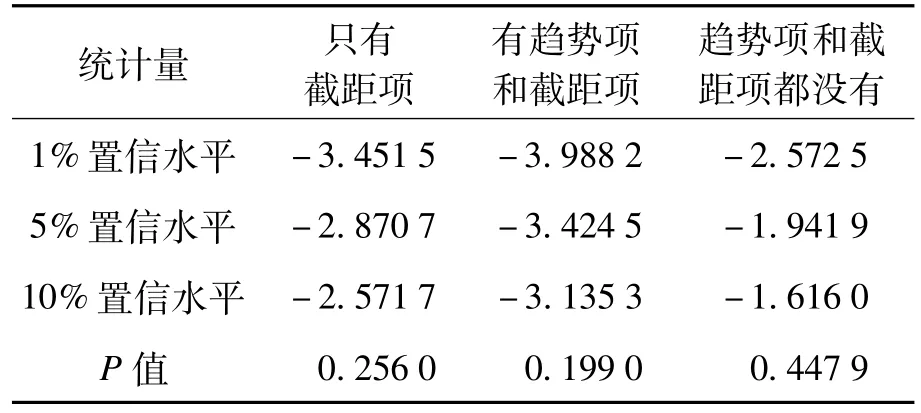
表1 差分前主要檢測指標結果

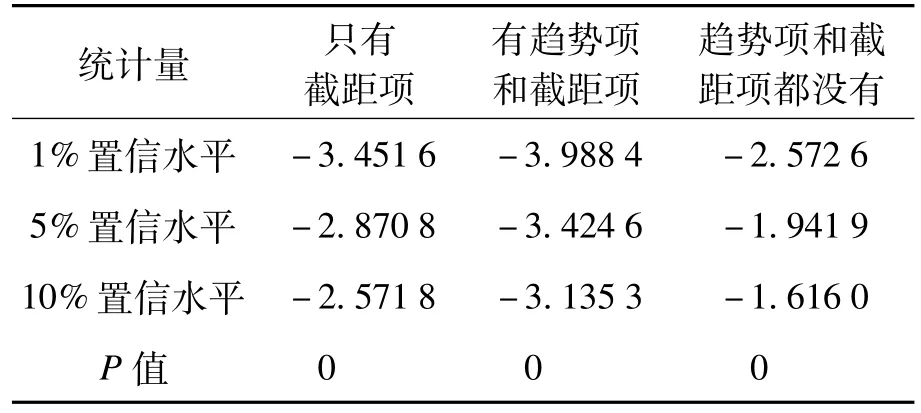
表2 差分后主要檢測指標結果

由表1、2的檢驗結果可知，原序列檢驗P＞ 0.05，說明原序列不穩定；一階差分后的序列檢驗P＜0.05，說明一階差分后的序列穩定，適合建立ARMA模型。

3．ARMA模型定階

利用Eviews 7.2，得出一階差分后序列自相關系數的3階截尾、偏相關系數2階截尾，初步斷定模型為ARMA（2，3）；再根據AIC和SC最小信息準則來準確確定模型階數［12］，選定ARMA（1，1），ARMA（1，2），ARMA（2，1），ARMA（2，2），ARMA（2，3）來進行比較，具體判定指標如表3所示。

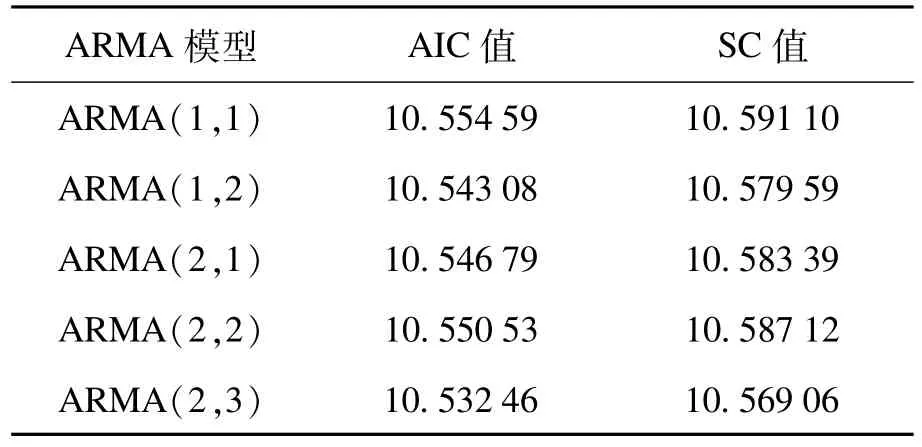
表3 ARM A模型相關判定指標

由表3可知，ARMA（2，3）模型的AIC值及SC值最小，根據最小信息準則該模型為最佳預測模型。利用OLS最小二乘法對模型進行檢驗，其中AR（1），MA（1）和MA（2）的P值明顯較大，統計上不顯著。剔除后再運用最小二乘法進行線性回歸，得出AR（2）和MA（3）的P＜0.05，統計上顯著，可以建立模型，即

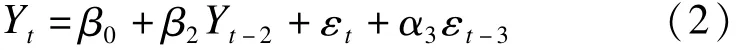
4．白噪聲檢驗

模型選定之后需要進行白噪聲檢驗，如果殘差序列的自相關均落入選定區域，則說明序列是白噪聲序列，再沒有需要提取的信息了；反之則不是殘差序列，需要進一步改進［13］。殘差檢驗結果如表4所示。

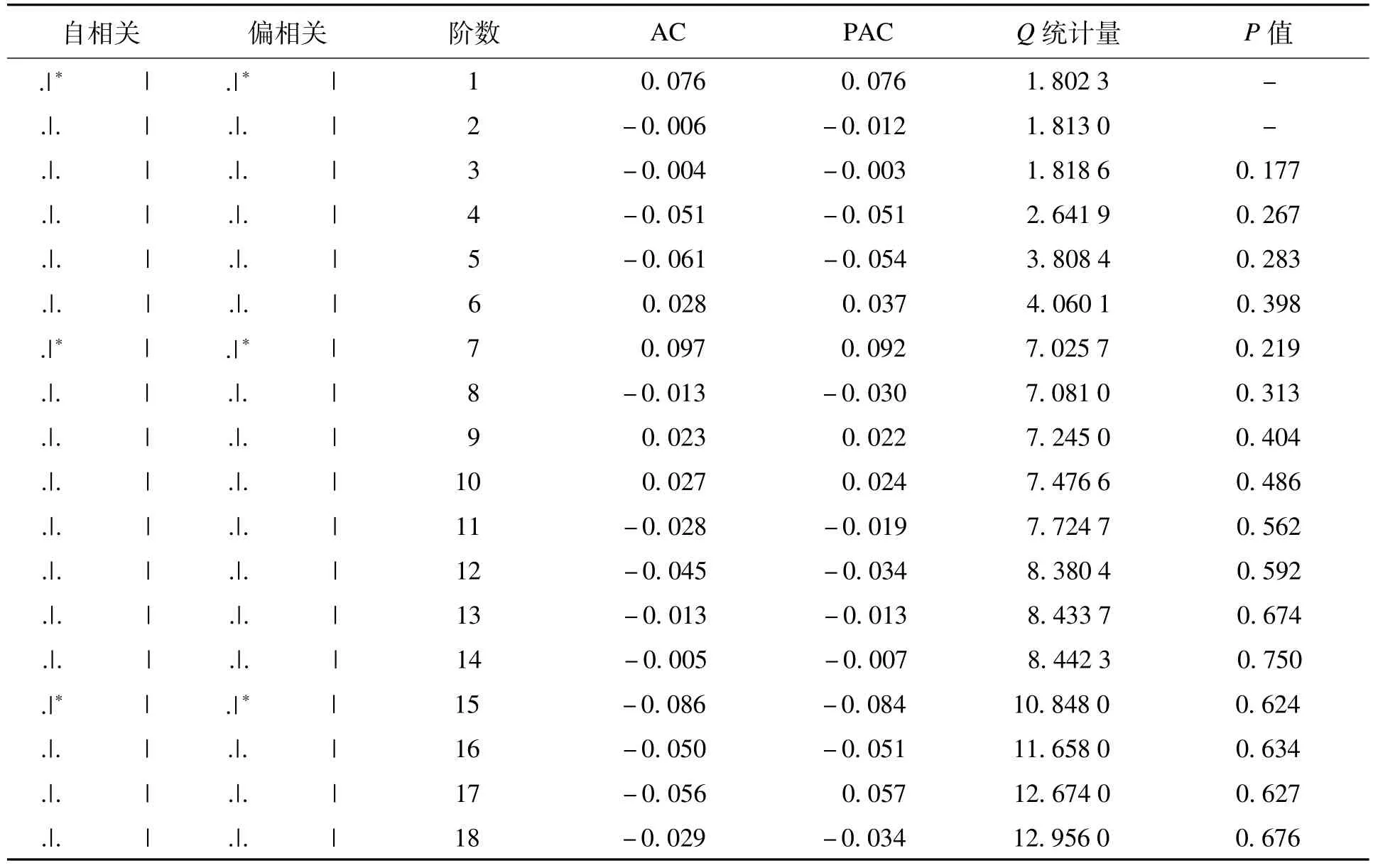
表4 殘差檢驗結果

由表4可知，殘差序列的自相關與偏相關均在選定區域內，且Q統計量的P值從3階開始都大于0.05，說明已建模型的隨機誤差相是白噪聲序列，可以用該模型進行價格預測。對模型進行OLS回歸，得出各項系數為c＝－1.296 0，AR（2）＝－0.122 9，MA（3）＝－0.144 6，則模型表達式為

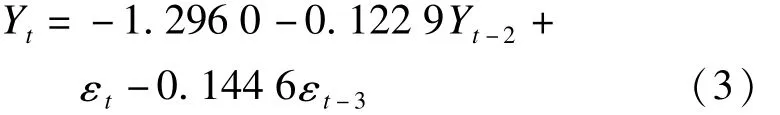
四、預測與檢驗

利用式（3）進行價格預測，得到真實期貨價格與預測期貨價格對比，如圖1所示。

由圖1可知，預測價格與真實價格整體走勢大致相同，說明預測結果具有一定的準確性。選出前5日大豆期貨價格預測值進行誤差檢驗，結果如表5所示。

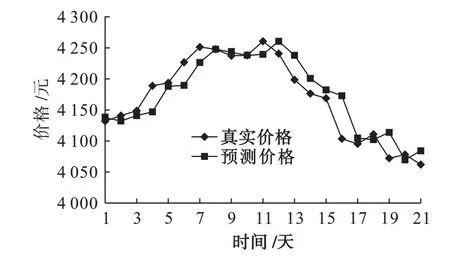
圖1 原數據與預測數據對比

如表5所示，2015－08－03—2015－08－07的期貨預測價格誤差率都很小，說明預測值比較接近真實值，此預測模型具有一定的有效性，能夠為投資者提供投資參考。

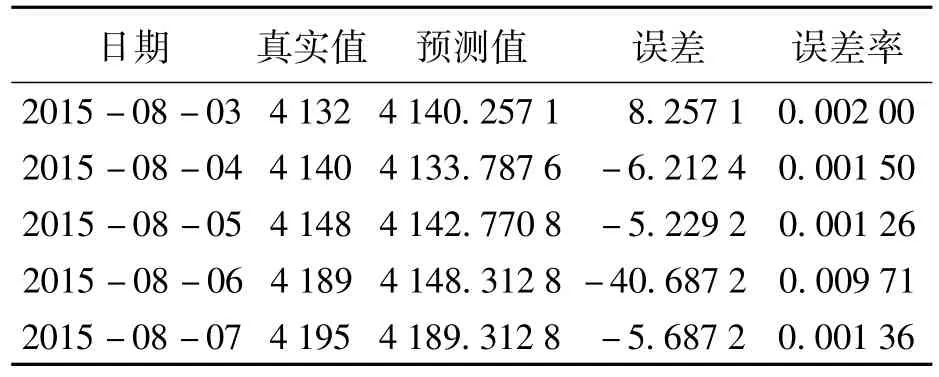
表5 部分預測值誤差率 元

五、結論與啟示

本文利用ARMA模型對2014－05－05—2015－08－31的大豆期貨時間序列數據進行實證分析，并進行模型預測效果檢驗。大豆期貨的時間序列數據是非平穩性數據，需要進行差分平穩化處理使其具有穩定性，再利用自相關與偏自相關系數進行模型定階，最后進行建模預測。預測結果表明，通過歷史時間序列數據對大豆期貨價格進行ARMA建模，所得預測價格與真實價格走勢大致相同，雖然有一定的誤差，但誤差率較小。該結果與已有研究相符，說明運用ARMA模型對大豆期貨價格進行短期預測具有一定的準確性，對進一步研究期貨價格預測問題具有一定輔助作用。

本文得出的預測價格與真實價格有一定誤差，為了使結果更有利于投資者，根據本文研究可得到如下啟示：

（1）綜合預測。價格信息具有多變性，結合技術面與基本面信息同時進行預測，可以降低誤差率，更有利于投資者。也可以在進行期貨投資的同時進行期權投資，這一方面可以在一定程度上規避金融市場風險性，另一方面可以從中獲得額外收益。

（2）由于ARMA模型是線性預測，為了使預測更有效，可以將線性預測與非線性預測結合起來，這將是下一步研究的重點。

（3）鼓勵更多的投資者進入期貨市場。更多的投資者進入期貨市場，會使市場更具競爭力，使價格的形成更具市場性。

［1］王一如，趙慶.大連期貨市場發展問題及對策研究［J］.現代商貿工業，2015（20）：127－129.

［2］馬保忠，甄博倩.基于時間序列分析的黃金期貨價格預測模型的實證分析［J］.商，2015（7）：152－155.

［3］Volkan E，Sertac A.ARIMA forecasting of primary energy demand by fuel in Turkey［J］.Energy Policy，2007（35）：1701－1708.

［4］Grudnitski G，Osburn L.Forecasting S＆P and gold futures prices：an application of neural networks［J］. Journal of Futures Markets，1993，13（6）：631－643.

［5］Hossain M Z，Samad Q A，A li M Z.ARIMA model and forecasting w ith three types of pulse prices in Bangladesh：a case study［J］.International Journal of Social Econom ics，2006，33（4）：344－353.

［6］李洛源.基于VAR方法的上海銀行間同業拆借利率風險度量［J］.經營管理者，2016（1）：26－27.

［7］梅志娟.ARMA-GARCH模型的期貨價格預測比較研究［J］.經濟研究導刊，2010，34（1）：73－74.

［8］閆冬.基于ARMA-GARCH模型的上證指數短期預測研究［J］.重慶理工大學學報（社會科學版），2012（10）：36－39.

［9］吳少華.縣域城市天然氣需求預測模型及其不均衡性對策研究［D］.鎮江：江蘇大學，2012.

［10］陳昭.時序非平穩性ADF檢驗法的理論與應用［J］.廣州大學學報（自然科學版），2008（5）：5－10.

［11］王博.基于ARMA-GARCH模型的上證指數實證分析［J］.科學技術與工程，2012（5）：1219－1221，1226.

［12］潘貴豪，胡乃聯，劉煥中，等.基于ARMA-GARCH模型的黃金價格實證分析［J］.黃金，2010（1）：5－8.

［13］李戰江，張昊，孫鵬哲，等.基于ARIMA模型的滬深300股指期貨價格預測研究［J］.魯東大學學報（自然科學版），2013（1）：22－24.

Em pirical study on price prediction of soybean futures

TENG Yong-ping，ZHOU Ting-ting
（School of Econom ics，Shenyang University of Technology，Shenyang 110870，China）

In the futuresmarket，the proper prediction of futures price is especially important whether for the enterprises to avoid risk by hedging，or for the investors to acquire profit by speculating.The data of soybean futures contract from May 5，2014 to August31，2015 are selected to conduct empirical analysis by applying statistic and econometric methods.Prediction is produced by applying ARMA model，and comparative chart of raw data and predicting data is acquired.This study proves that the forecasting mechanism of short-term price based on ARMA model has certain accuracy，and can provide reference for investors.

soybean；futures price；price prediction；ARMA model；unit root test；time series analysis；white noise test

F 831.5

：A

：1674－0823（2017）04－0331－04

10.7688／j.issn.1674－0823.2017.04.07

（責任編輯：郭曉亮）

2016－07－06

遼寧省財政科研基金項目（15B03）。

滕永平（1962－），男，山東榮成人，教授，主要從事金融市場學等方面的研究。

*本文已于2016－11－29 09∶09在中國知網優先數字出版。網絡出版地址：http：∥www.cnki.net／kcms／detail／21.1558.C. 20161129.0909.014.htm l