一種基于椋鳥群行為的改進型蝙蝠算法

胡 飛, 孫自強

(華東理工大學化工過程先進控制和優化技術教育部重點實驗室,上海 200237)

一種基于椋鳥群行為的改進型蝙蝠算法

胡 飛, 孫自強

(華東理工大學化工過程先進控制和優化技術教育部重點實驗室,上海 200237)

蝙蝠算法是一種新興的元啟發式算法,基本蝙蝠算法(BA)存在尋優精度低、易陷入局部最優等缺點。將椋鳥群的集體性行為引入到基本蝙蝠算法中,有效地提高了算法的搜索范圍;引入線性遞減權重,用于平衡全局搜索和局部搜索。通過一些測試函數對該算法進行仿真研究,結果表明改進的蝙蝠算法有效地避免了種群個體陷入局部最優,提高了算法的尋優精度,優化效果得到改善。

蝙蝠算法(BA); 椋鳥群行為; 權重; 局部最優

蝙蝠算法是一種新興的元啟發優化算法,該算法可以看作是和聲搜索算法和粒子群算法的混合[1]。目前,已有許多經典的優化算法應用于諸多方面。文獻[2]將一種改進的混沌蜂群算法應用于流水車間調度,優化調度過程中的最大完成時間,優化效果較好。文獻[3]針對化工過程的動態多目標問題,利用一種改進型粒子群算法對其進行優化,測試結果表明該算法能較好地解決工程問題。蝙蝠算法作為新興的優化算法,同樣具有較好的應用前景,已經廣泛應用于工程和自然科學領域,如函數優化問題、生產調度問題以及多目標優化問題等。文獻[4]將蝙蝠算法應用于一些工程函數尋優,結果表明該算法尋優精度較高。文獻[5]將蝙蝠算法應用于混合流水車間調度問題,能夠最小化車間調度的完工時間。文獻[6]針對多目標優化問題提出了一種多目標蝙蝠算法,應用于一些多目標函數優化,尋優效果較佳。然而蝙蝠算法亦具有粒子群等優化算法的通病,即收斂速度慢、容易陷入局部最優、搜索精度較低。為了提高蝙蝠算法的控制效果,許多研究者對蝙蝠算法開展研究,并對其進行改進。劉長平等[7]提出基于Lévy飛行特征的蝙蝠算法,從算法仿生原理入手,采用Lévy飛行搜索策略,更真實地模擬蝙蝠的捕食行為。Topal 等[8]提出一種動態虛擬蝙蝠算法,將蝙蝠種群分成探索類和開拓類子種群,當探索類蝙蝠進行對外搜索最優值時,開拓類蝙蝠進行局部搜索,尋找最優值。李枝勇等[9]將量子計算引入到蝙蝠算法中,利用量子位對蝙蝠的位置進行編碼,利用量子旋轉門進行蝙蝠最優位置的搜索。Gandomi 等[10]提出具有混沌搜索策略的蝙蝠算法,并利用不同的混沌函數產生的混沌序列對精英個體進行混沌優化,驗證了混沌策略的有效性。Niknam 等[11]提出了一種自適應蝙蝠算法,將自適應方法與蝙蝠算法結合,提高算法的種群多樣性及搜索能力,并應用于電力系統中UC問題,能夠快速解決UC問題。Wang等[12]提出將差分進化算法與蝙蝠算法相結合,并用于解決UCVA三維路徑規劃問題,結果表明控制效果較好。

當前針對蝙蝠算法的改進主要有兩個方面:(1)針對蝙蝠算法自身機理存在的變量進行改進,包括參數自適應、輔助參數的引入以及搜索策略等;(2)將其他的優化算法與蝙蝠算法相結合,提高基本蝙蝠算法的控制效果[13]。本文提出的改進策略屬于第1種,將椋鳥群行為引入到蝙蝠算法中,當全局最優值陷入局部最優時,根據椋鳥群的集體性行為對蝙蝠的位置和速度進行更新。

1 基本蝙蝠算法

1.1基本蝙蝠算法的位置和速度更新

將蝙蝠類比為在當前可行域內分布的搜索點,用目標函數值(適應度函數值)的大小來判斷當前蝙蝠所處位置的優劣;將蝙蝠飛行移動探測目標的過程類比為搜索目標函數位置最優解的過程,則可用以下流程和公式來模擬蝙蝠回聲定位的行為[14]。初始時刻,需對蝙蝠的頻率進行初始化,同時,蝙蝠在飛行過程中也需對其速度和位置進行更新,兩者的更新公式如式(1)～ 式(3)所示。

(1)

(2)

(3)

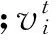
在搜索過程中還需進行局部搜索,公式如下:

(4)

其中:xnew為蝙蝠更新后的位置;xold為蝙蝠更新前的位置;ε∈[-1,1]為隨機數;At為整個蝙蝠種群在t時刻的平均響度。

1.2響度和脈沖發射率

在蝙蝠搜尋目標獵物時,需對響度Ai和脈沖發射率ri進行更新。初始階段,Ai較大,ri較小,搜尋到目標獵物后,Ai減小,ri增大[15]。Ai和ri更新公式如下:

(5)

(6)

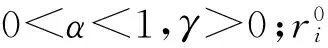
2 改進的蝙蝠算法

2.1椋鳥群行為

椋鳥是一種群體性種群,在日常生活中會產生一些壯觀的景象。當遇到天敵時,其中一些個體會改變飛行方向,并影響周圍個體,如此使得整個種群方向迅速改變,從而躲避天敵的捕食。

由于每個個體都會與周圍的個體交流信息,因此由該個體發出的信息會很快傳播至整個種群,這種行為稱為椋鳥群行為。在椋鳥群中,椋鳥個體一般與其附近的7個個體進行信息交流,這7個個體再分別與其附近的7個個體進行信息交流,進而遍布整個種群,達到整個種群的信息共享。一項分析表明,6個或7個個體組成一個群體交流網絡將有效平衡整個種群凝聚性及個體交流,因此個體與其附近的7個個體進行信息交流足以影響整個種群的行為[16]。

2.2引入椋鳥群行為的蝙蝠算法[17](SFBA)

基本蝙蝠算法在搜索過程中易陷入局部最優,缺乏種群多樣性。將椋鳥群行為引入基本蝙蝠算法中,有助于增加種群多樣性,避免陷入局部最優。當種群迭代結果發生停滯或更差超過上限值(count_limit)時,挑選出一定數目(max_num)適應度值較差的個體,對這些個體的位置和速度進行變換,挑選出全局最優值,替換原先的種群全局最優值。

針對位置變換,依據式(7)對粒子i的位置進行更新。

(7)

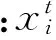
針對速度變換,依據式(8)對粒子i的速度進行更新。

(8)

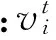
2.3針對位置和速度引入權重

由于固定的慣性權重控制精度不高,控制效果較差,本文針對蝙蝠算法速度和位置更新公式,分別引入權重w1和w2,見式(9)和式(10)。將權重w1由固定權重變為線性遞減權重。起初權重較大,加強全局搜索,隨著迭代次數的增加,迭代后期,權重減小,有利于提高局部搜索能力。線性遞減的權重公式如下:

(9)

(10)

(11)

其中:wmax為w1的上限值;wmin為w1的下限值;Iter為當前迭代次數;Iter_max為最大迭代次數。

2.4SFBA算法流程

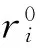
(2) 對所有蝙蝠個體計算適應度函數值f(x),找出當前位置最優解x*。

(3) 按照式(1)隨機產生頻率的新解。

(4) 根據式(9)和式(10)對蝙蝠的速度和位置進行更新,針對速度設置的權重w1使用線性遞減權重,見式(11)。

(5) 產生一個隨機值rand,若rand大于脈沖發射率ri,則根據式(4),從處在最佳位置的蝙蝠i個體中選取一個解,對該位置最優解進行隨機擾動,產生一個局部解xnew替代蝙蝠i的當前位置。

(6) 計算適應度函數值(目標函數值);

(7) 若隨機值rand小于響度Ai且更新位置后的目標函數值小于當前目標函數最優值,則接受這個位置新解,并增大脈沖發射率ri和響度Ai,見式(5)、式(6)。

(8) 對位置變動后的蝙蝠重新排列,找出當前位置最優解和適應度函數最優值。

(9) 判斷當前適應度最優值是否大于或等于上一代適應度最優值,若是,則計數器count+1(count初始值設為0)。

(10) 判斷count是否大于上限值count_limit,若是,則挑選出適應度較差的max_num個個體,利用式(7)與式(8)更新該部分個體位置和速度值,替換原先個體最優值,并從中找出全局最優值,作為當前種群全局最優值,并置count=0。

(11) 當迭代次數小于最大迭代次數時,回到步驟(2)繼續迭代搜索最優解。

(12) 算法迭代結束,輸出位置全局最優解。

3 算法的參數選擇

SFBA算法參數主要包含w1,w2,count_limit,max_num,其中w1主要由wmax和wmin決定,因此需要選擇的參數主要為wmax,wmin,w2,count_limit,max_num,這5個參數可以通過實驗確定。以Sphere函數為基準進行實驗,種群規模設為100,迭代次數Iter_max為500次,分別運行20次,取20次優化結果的平均值作為參考值,確定權值wmax,wmin以及w2的最優值。

表1示出了wmax為0.45、0.46、0.47、0.48、0.49、0.50、0.51、0.52、0.53、0.54、0.55,wmin=0.1,w2=0.50時的運行結果,可以看出,wmax=0.50時算法控制效果較好。

表2示出了wmin為0.05、0.06、0.07、0.08、0.09、0.10、0.11、0.12、0.13、0.14、0.15,wmax=0.50,w2=0.50時的運行結果,可以看出,wmin=0.10時算法控制效果較好。

表3示出了w2為0.45、0.46、0.47、0.48、0.49、0.50、0.51、0.52、0.53、0.54、0.55,wmax=0.50,wmin=0.10時的運行結果,可以看出,w2=0.50時算法控制效果較好。

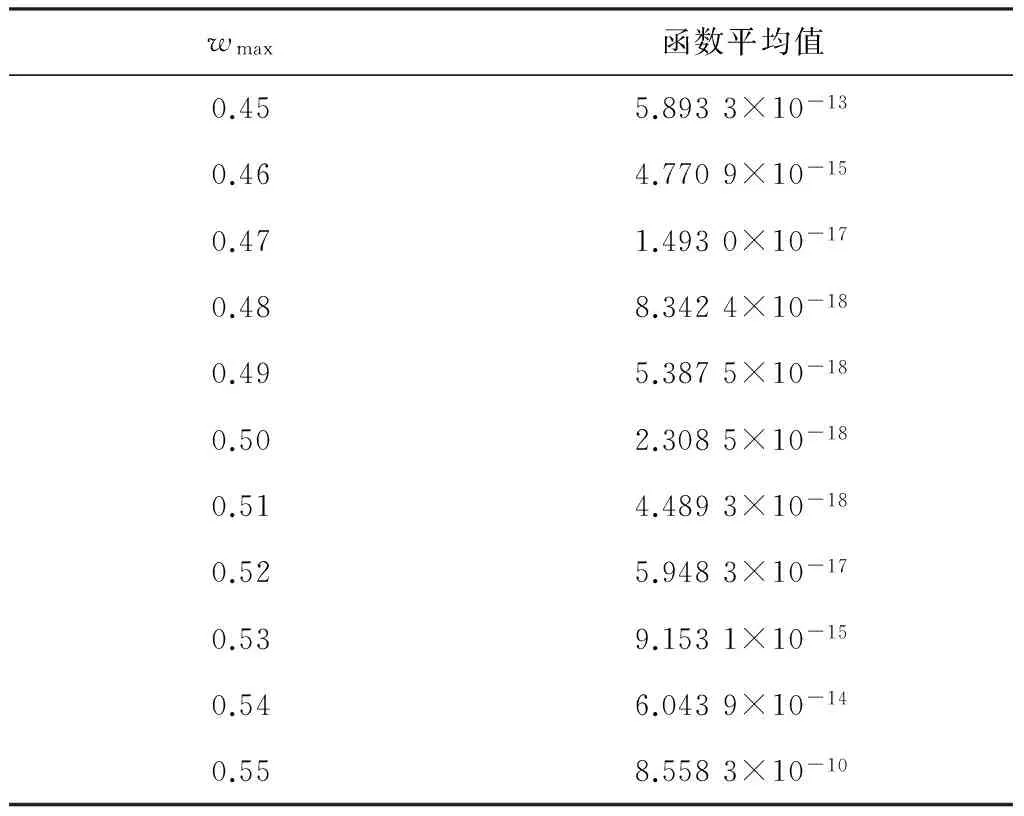
表1 wmax參數取值表Table 1 Parameter value table of wmax

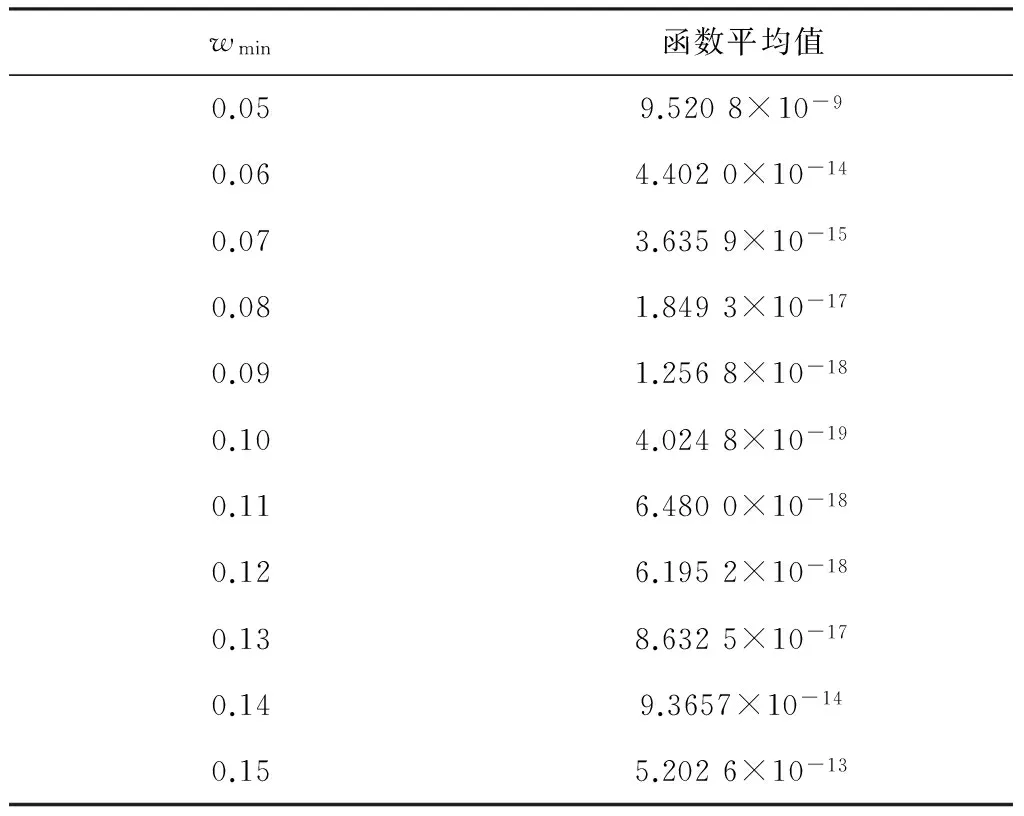
表2 wmin參數取值表Table 2 Parameter value table of wmin

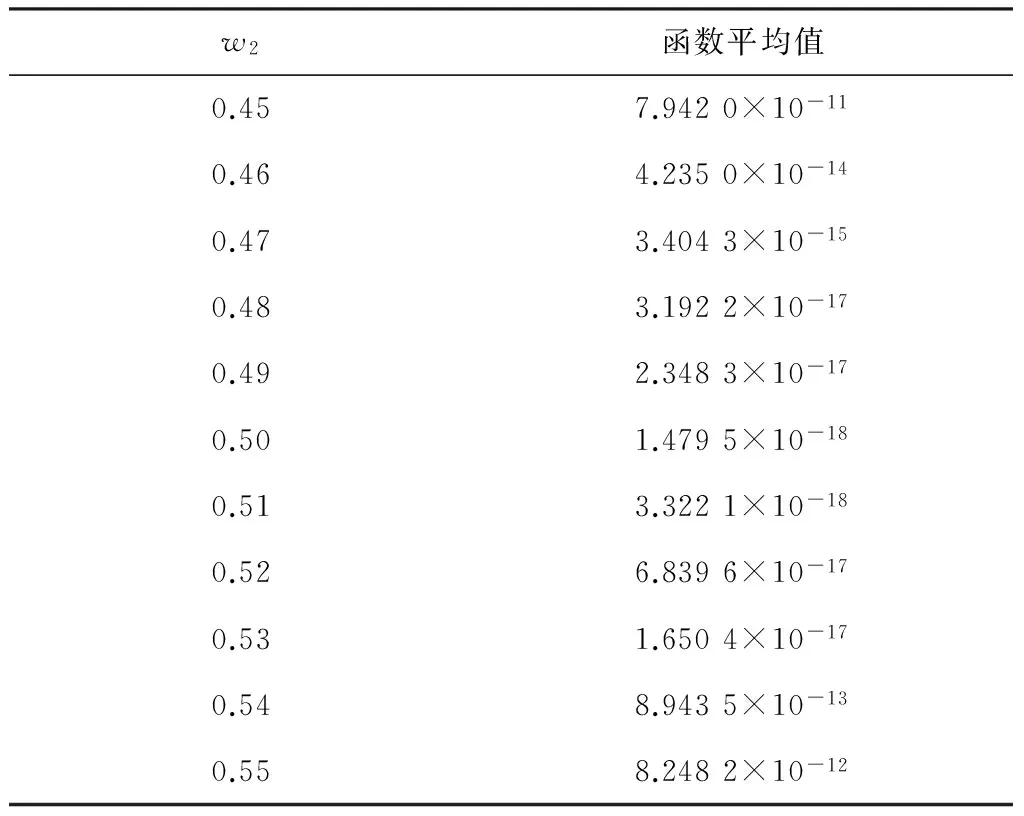
表3 w2參數取值表Table 3 Parameter value table of w2

表4示出了count_limit為1、2、3、4、5時的運行結果,可以看出,count_limit=3時算法控制效果較好。

表5示出了max_num為13、17、19、22、23時的運行結果,可以看出,max_num=19時算法控制效果較好。

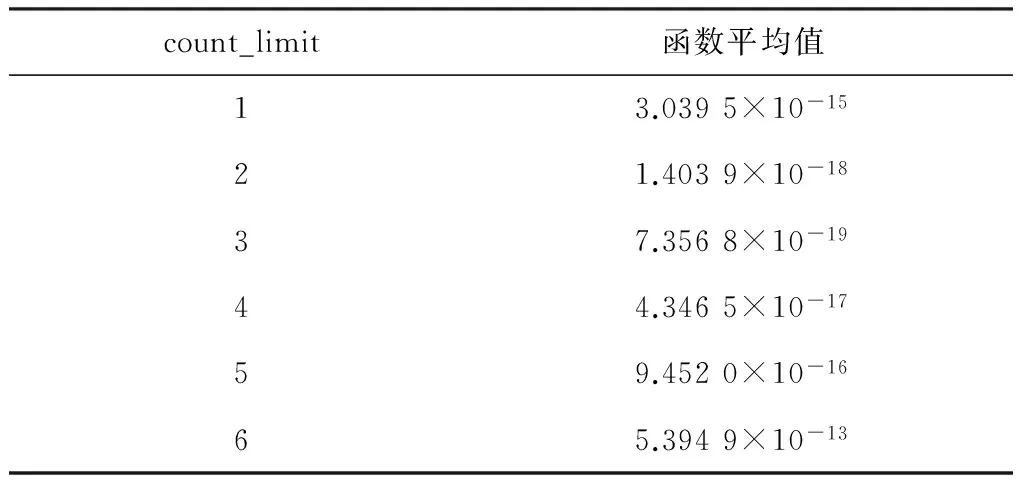
表4 count_limit參數取值表Table 4 Parameter value table of count_limit

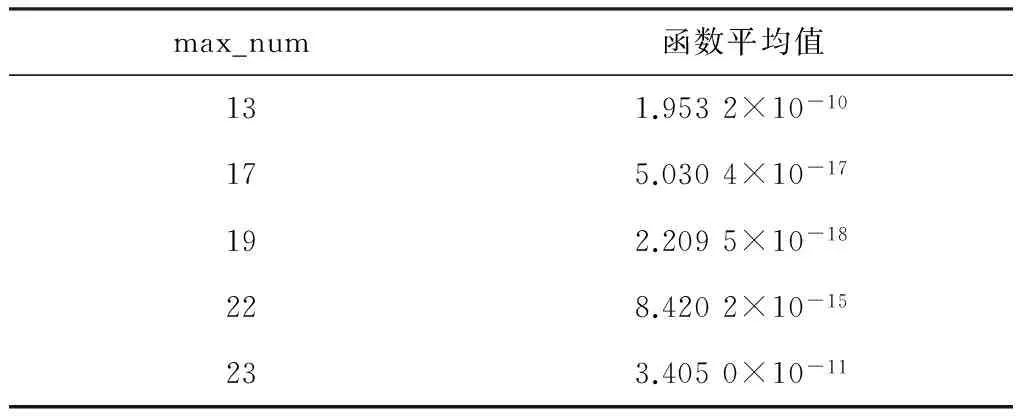
表5 max_num參數取值表Table 5 Parameter value table of max_num

綜上所述,對于改進型蝙蝠算法,取wmax=0.50,wmin=0.10,w2=0.50,count_limit=3,max_num=19,采用這組參數進行算法測試,可以進一步驗證改進型蝙蝠算法的可行性。

4 測試結果

為了評估本文提出的改進型蝙蝠算法的尋優效果,選擇5個標準測試函數(如表6所示)進行測試。

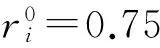
表6 標準測試函數Table 6 Benchmark functions

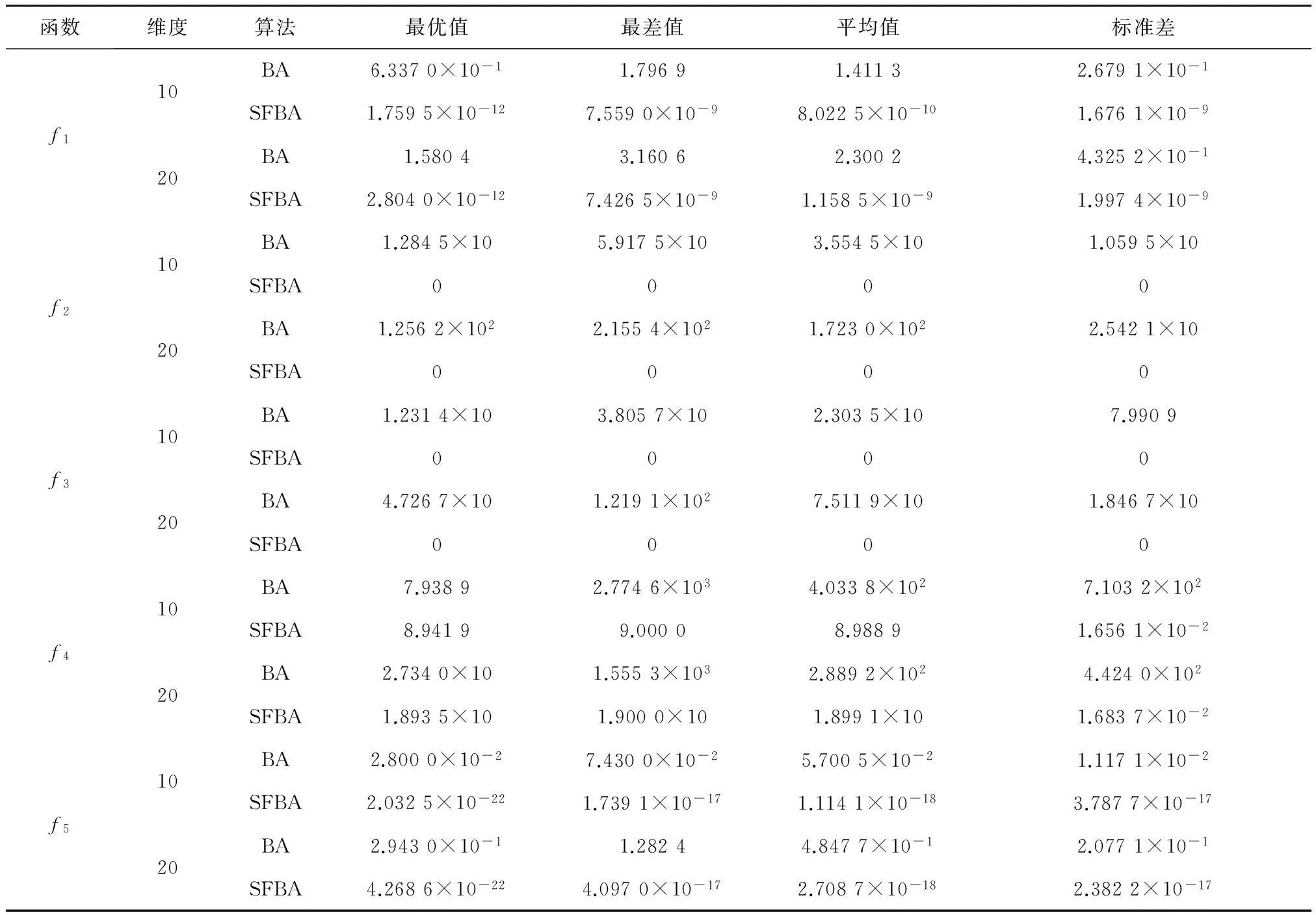
表7 標準測試函數尋優結果對比Table 7 Comparison of Benchmark functions optimization results

測試函數f1,f2,f3均為多峰值測試函數,BA尋優精度較低,控制效果較差,而SFBA均能取得較高的尋優精度,控制效果較好。測試函數f4是一種典型的病態非凸單模函數,難以極小化,從表7中數據可以看出BA和SFBA尋優效果均不理想。測試函數f5為簡單的單峰值函數,在自變量取值范圍內僅有一個全局極小值點,因而BA的尋優效果還可以,但是相比之下,SFBA的尋優精度更高,控制效果更好。限于篇幅,本文僅給出部分維度的尋優效果,測試函數迭代曲線對比如圖1～圖5所示。

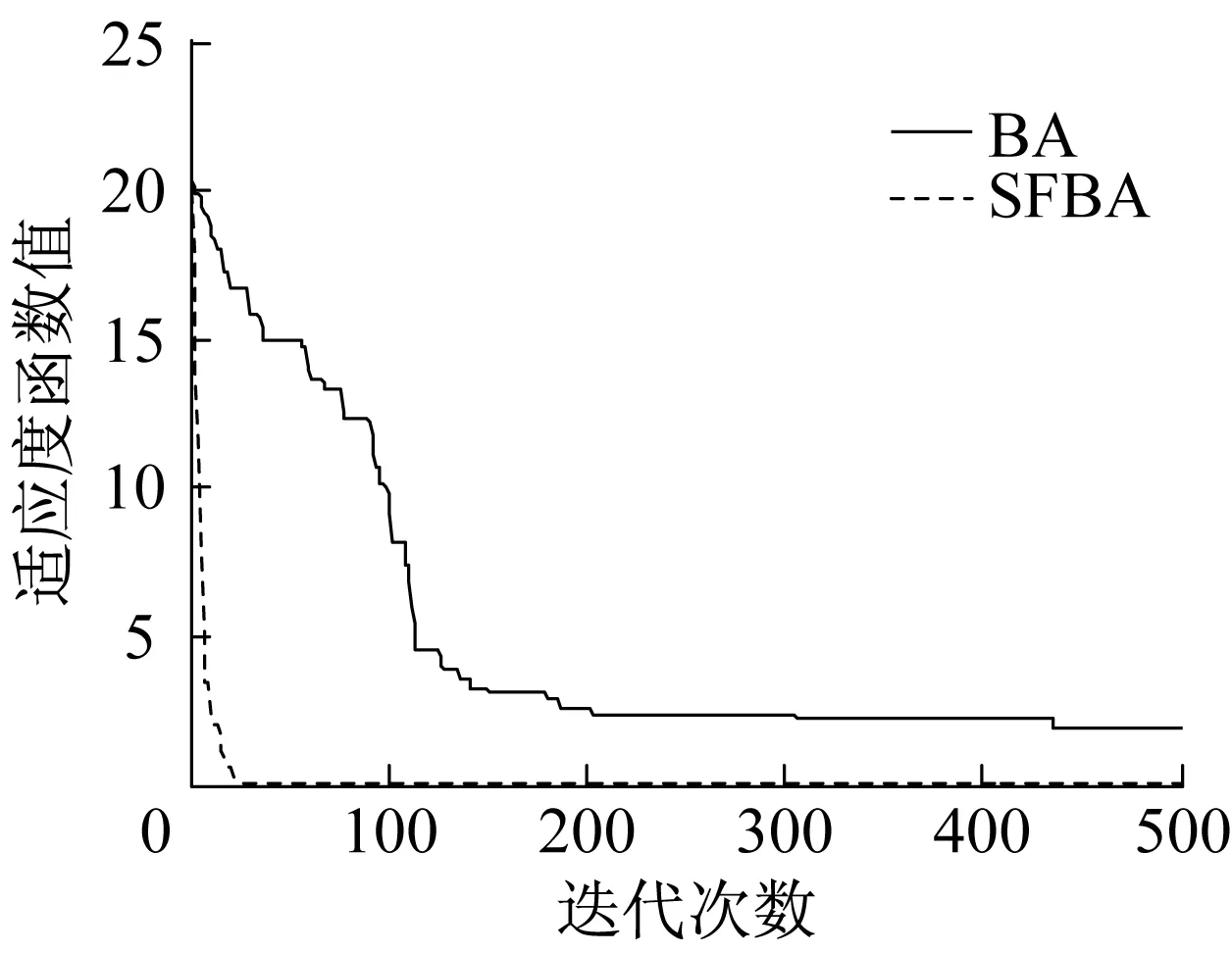
圖1 測試函數f1迭代曲線對比(d=20)Fig.1 Comparison of Benchmark functionf1′s iterative curves (d=20)

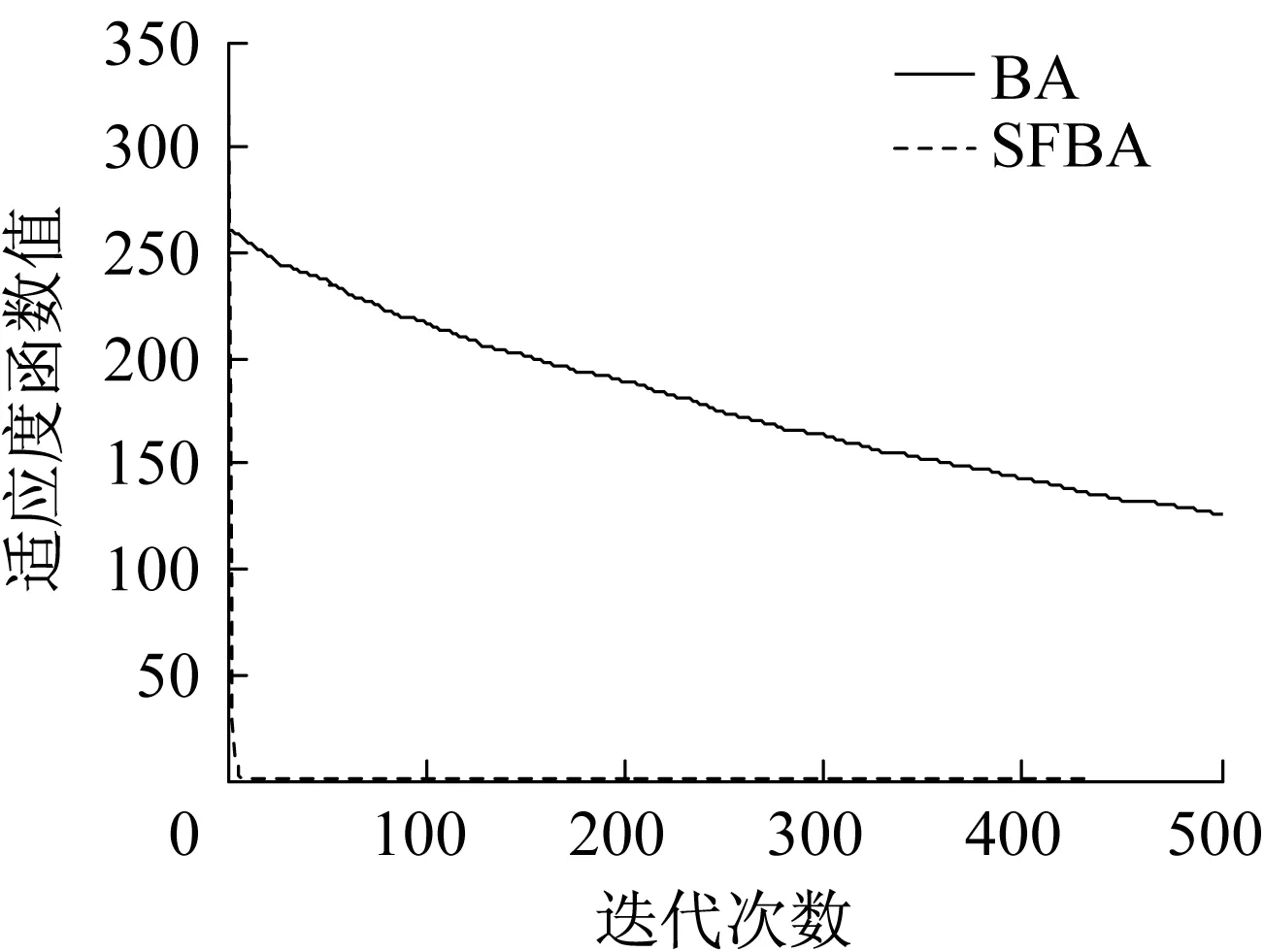
圖2 測試函數f2迭代曲線對比(d=20)Fig.2 Comparison of Benchmark functionf2′s iterative curves (d=20)

為了進一步驗證本文算法的可行性,將SFBA與文獻[18]基于微分算子與Lévy飛行策略的蝙蝠算法(DLBA)及文獻[19]基于遺傳交叉因子的蝙蝠算法(GHBA)進行對比,結果如表8所示。從表8中數據可知,SFBA的尋優效果優于GHBA、DLBA。

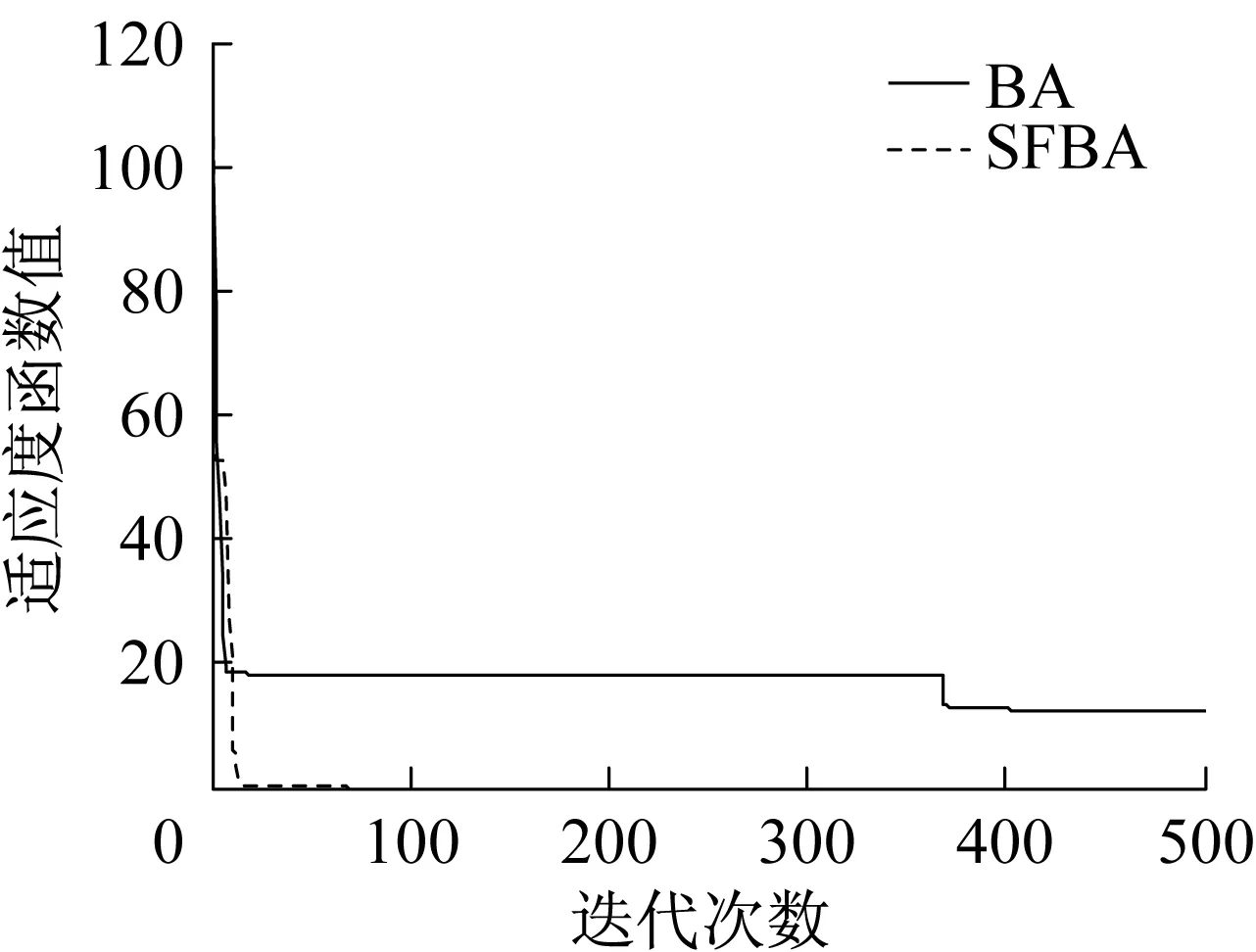
圖3 測試函數f3迭代曲線對比(d=10)Fig.3 Comparison of Benchmark functionf3′s iterative curves (d=10)

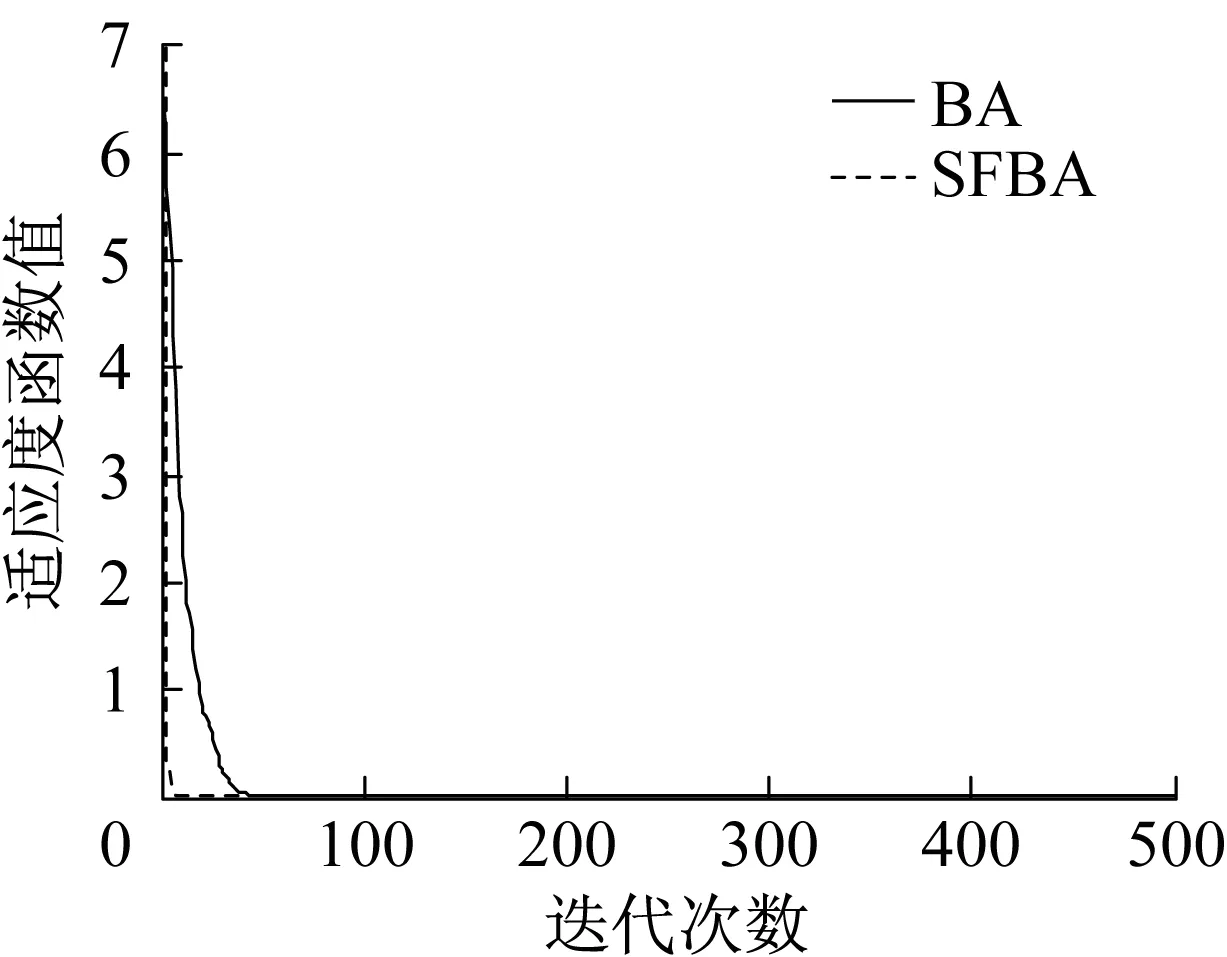
圖4 測試函數f4迭代曲線對比(d=10)Fig.4 Comparison of Benchmark functionf4′s iterative curves (d=10)

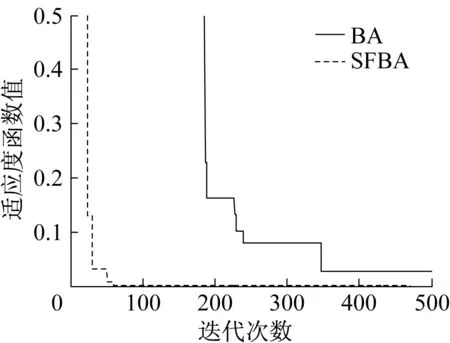
圖5 測試函數f5迭代曲線對比(d=10)Fig.5 Comparison of Benchmark functionf5′s iterative curves (d=10)表8 改進的BA算法在5個測試函數尋優結果對比Table 8 Comparison of improved BA algorithms in 5 Benchmark function optimization results

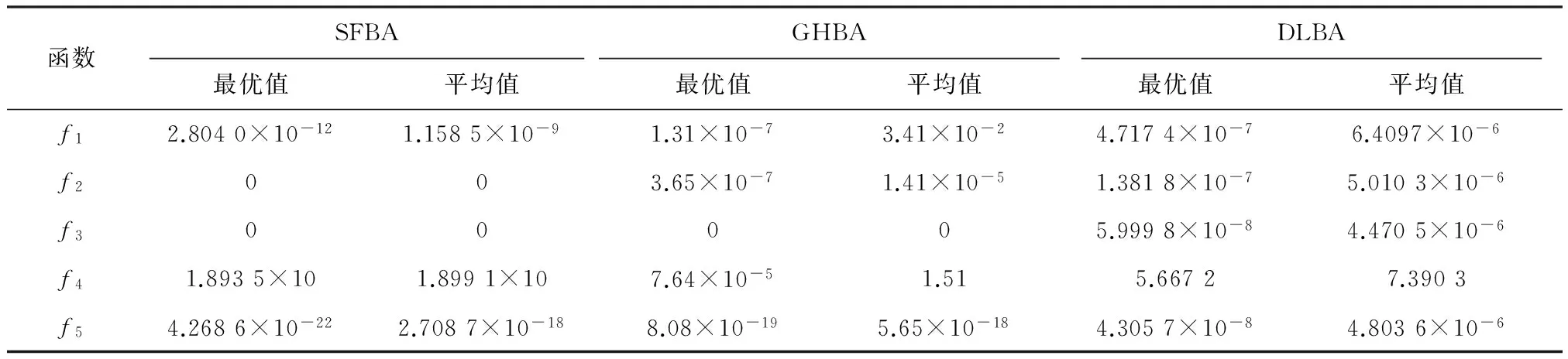
函數SFBAGHBADLBA最優值平均值最優值平均值最優值平均值f12.8040×10-121.1585×10-91.31×10-73.41×10-24.7174×10-76.4097×10-6f2003.65×10-71.41×10-51.3818×10-75.0103×10-6f300005.9998×10-84.4705×10-6f41.8935×101.8991×107.64×10-51.515.66727.3903f54.2686×10-222.7087×10-188.08×10-195.65×10-184.3057×10-84.8036×10-6

5 改進型蝙蝠算法在PID參數整定中的應用

為了進一步驗證本文算法的有效性,將改進型蝙蝠算法應用于PID控制器參數優化中[20]。選取二階被控對象,傳遞函數如下:

(12)

采樣時間為2 ms,輸入一個階躍信號,采用誤差絕對值時間積分性能指標作為參數選擇的最小目標函數,為防止能量過大,在目標函數中加入控制輸入平方項,最優指標如式(13)所示。

(13)

式中:J表示目標函數;e(t)表示系統誤差;u(t)為控制器輸出;tu為上升時間;w1,w2,w3為權重值。

為避免超調,采取懲罰功能,一旦出現超調,就將超調量作為最優指標中的一項,此時最優指標如式(14)所示。

ifey(t)<0

(14)

其中:w4為權重值,且w4>>w1;ey(t)=y(t)-y(t-1),y(t)為被控對象輸出。

SFBA算法中,種群數為100,wmax=0.50,wmin=0.10,w2=0.5,count_limit=3,max_num=19,PID參數Kp,Ki,Kd取值范圍分別為[0,40],[0,4],[0,4],取w1=0.999,w2=0.001,w3=100,w4=2.0。迭代100次后,用BA算法優化PID三參數優化后Kp=31.711 6,Ki=3.354 7,Kd=0.147 2,性能指標J=79.189 6,適應度函數J、Kp、Ki、Kd的優化過程如圖6所示。用SFBA算法優化PID三參數優化后Kp=35.053 4,Ki=3.527 6,Kd=0.003 1,性能指標J=78.352 7,適應度函數J,Kp,Ki,Kd的優化過程如圖7所示。BA和SFBA算法優化后,PID控制階躍響應如圖8所示。

由圖8可知,SFBA算法優化效果優于BA算法,SFBA基本無超調,調節時間較短,響應速度較快。

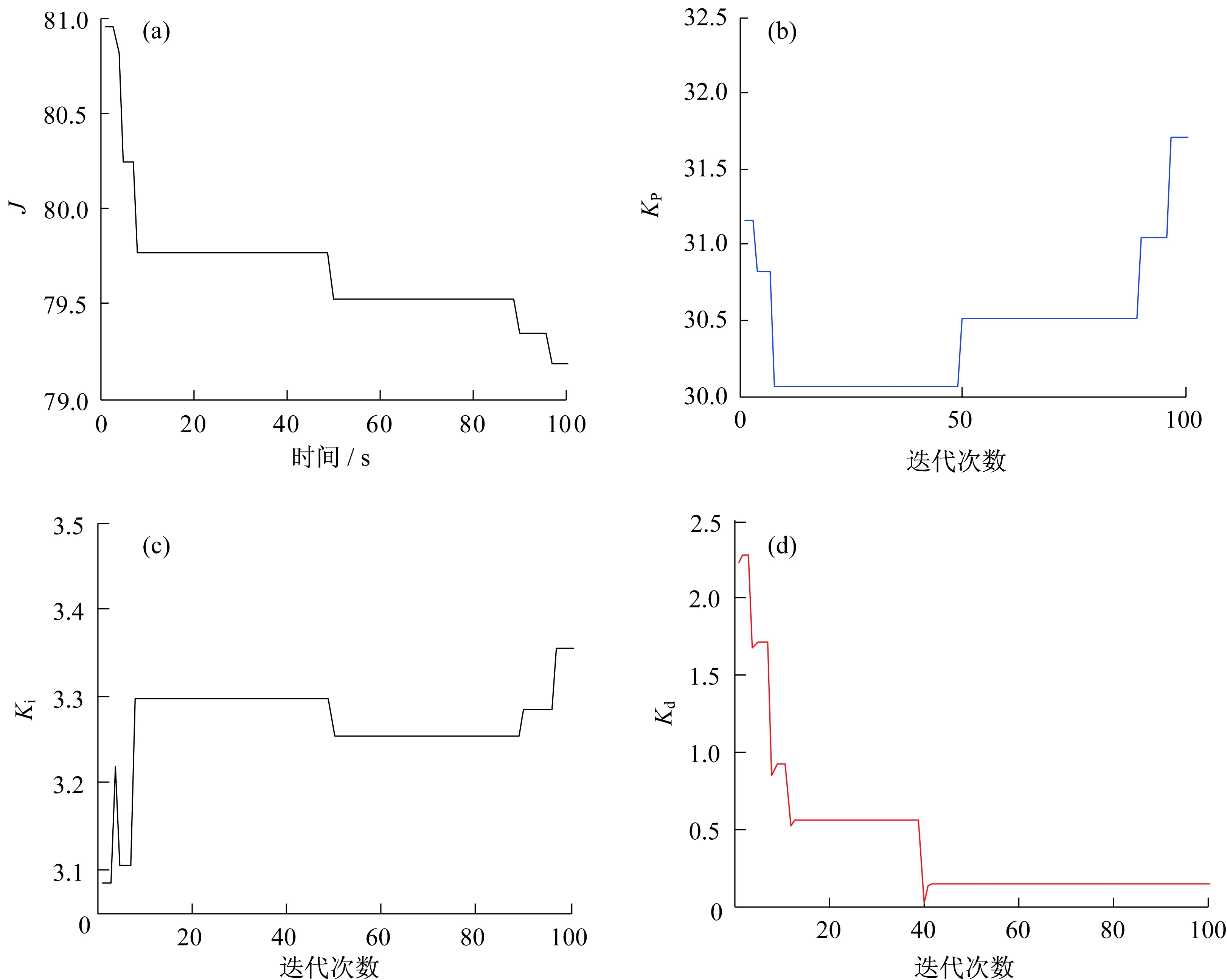
圖6 BA算法迭代曲線Fig.6 Iterative curves of BA algorithm

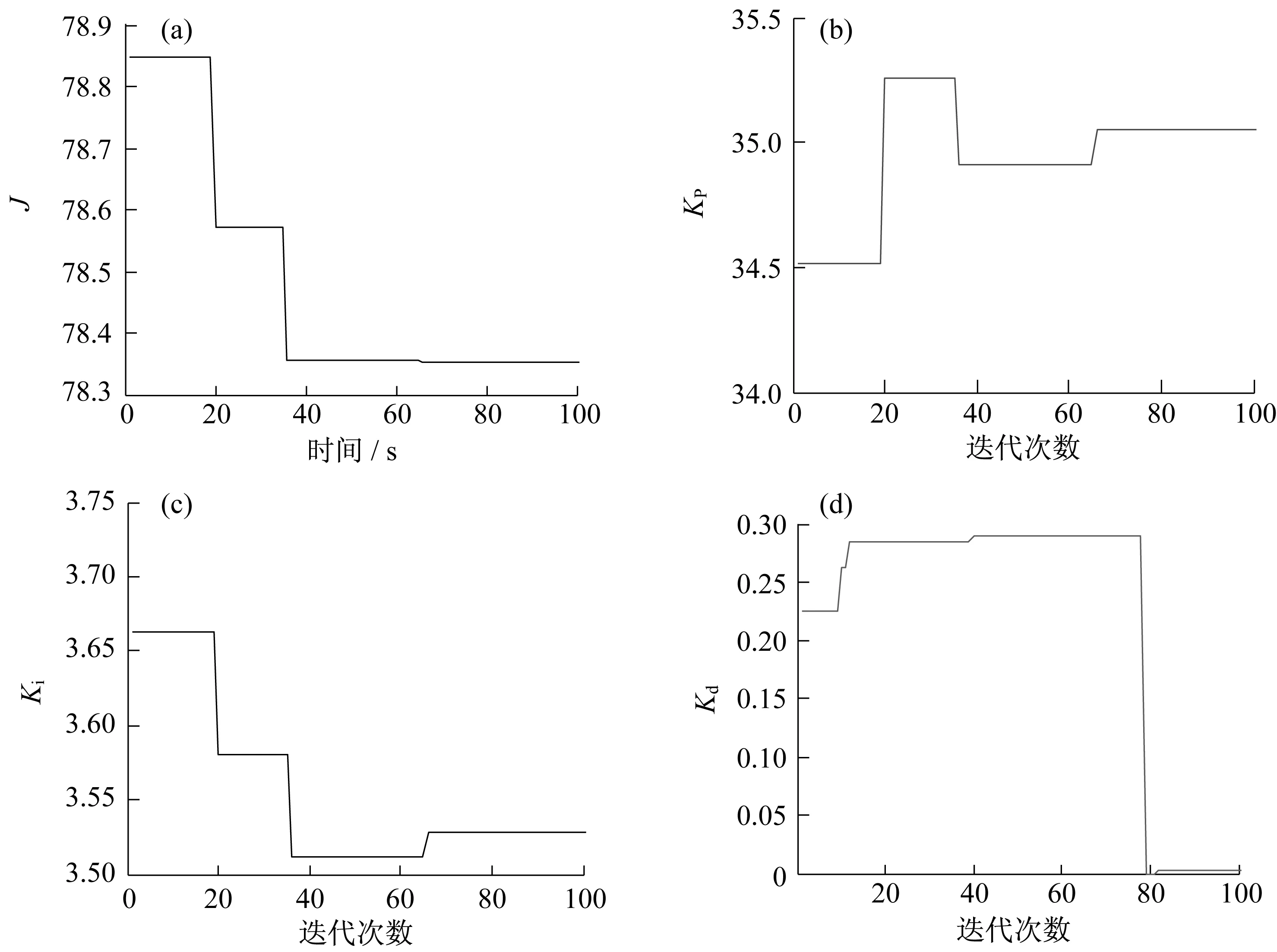
圖7 SFBA算法的迭代曲線Fig.7 Iterative curves of SFBA algorithm

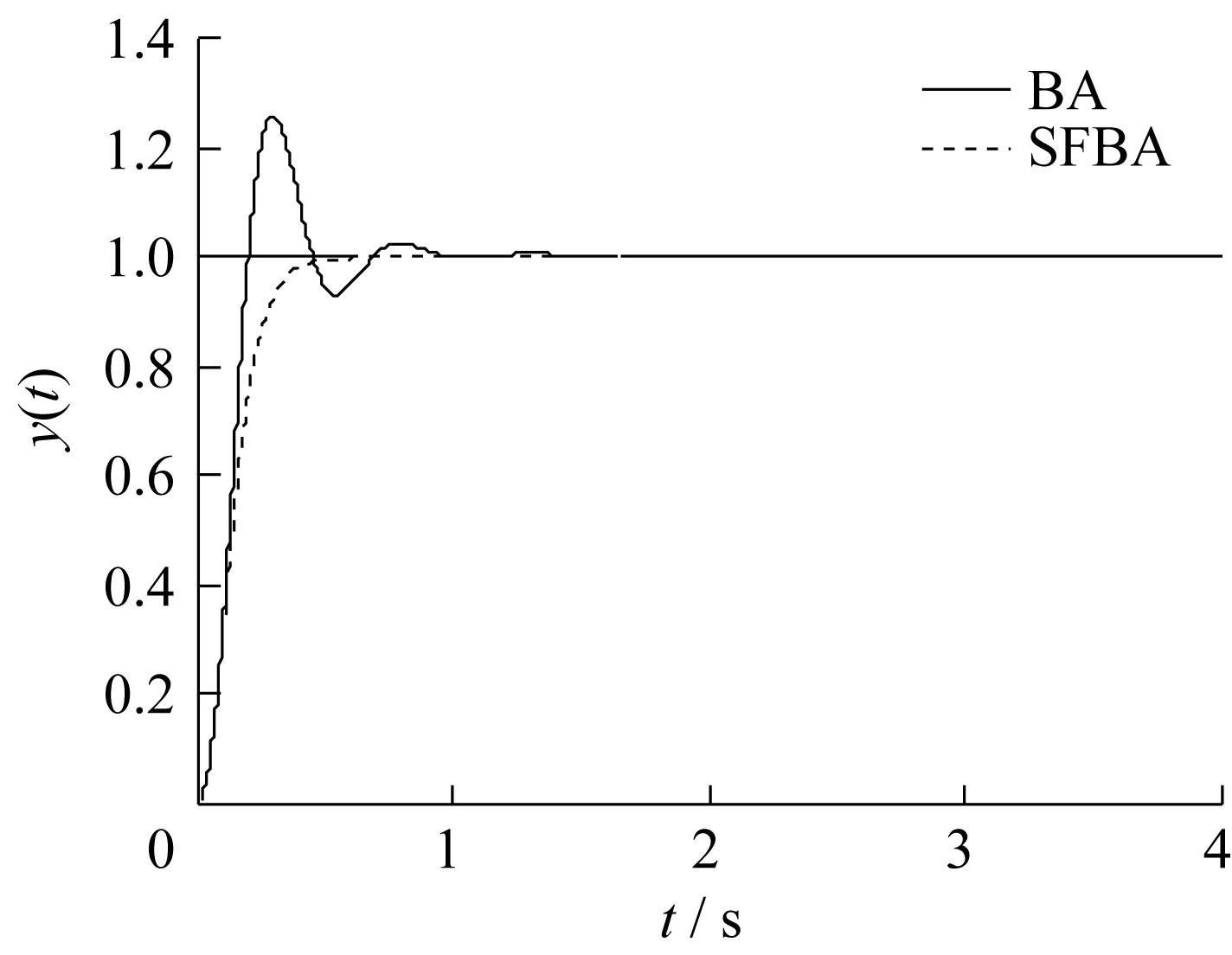
圖8 BA算法與SFBA算法的階躍響應曲線Fig.8 Unit-step response of BA algorithm and SFBA algorithm

6 結 論

本文針對BA算法收斂速度慢、容易陷入局部最優、搜索精度不高等缺點,提出了一種基于椋鳥群行為的蝙蝠算法(SFBA),同時引入線性遞減權重平衡全局搜索與局部搜索。通過5個不同的單峰值和多峰值測試函數進行驗證,與BA算法相比,SFBA算法優化效果較佳。此外,將SFBA算法應用于PID參數優化,結果表明SFBA算法優化效果優于BA算法。

[1] YANG X S.A new metaheuristic bat-inspired algorithm[J].Physics,2010,284:65-74.

[2] 劉華,顧幸生.改進的混沌蜂群算法在流水線調度中的應用[J].華東理工大學學報(自然科學版),2013,39(3):345-350.

[3] 王珊珊,杜文莉,陳旭,等.基于約束骨干粒子群算法的化工過程動態多目標優化[J].華東理工大學學報(自然科學版),2014,40(4):449-457.

[4] YANG X S,GANDOMI A H.Bat algorithm:A novel approach for global engineering optimization[J].Engineering Computation,2012,29(5):267-289.

[5] MARICHELVAM M K,PRABAHARAN T,YANG X S,etal.Solving hybrid flow shop scheduling problems using bat algorithm[J].International Journal of Logistics Economics & Globalisation,2013,5(1):15-29.

[6] YANG X S.Bat algorithm for multi-objective optimization[J].International Journal of Bio-Inspired Computation,2011,3(5):267-274.

[7] 劉長平,葉春明.具有 Lévy飛行特征的蝙蝠算法[J].智能系統學報,2013(3):240-246.

[8] TOPAL A O,ALTUN O.A novel meta-heuristic algorithm:Dynamic virtual bats algorithm[J].Information Sciences,2016,354:222-235.

[9] 李枝勇,馬良,張惠珍.函數優化的量子蝙蝠算法[J].系統管理學報,2014(5):717-722.

[10] GANDOMI A H,YANG X S.Chaotic bat algorithm[J].Journal of Computational Science,2014,5(2):224-232.

[11] NIKNAM T,BAVAFA F,AZIZIPANAH-ABARGHOOEE R.New self-adaptive bat-inspired algorithm for unit comi--tment problem[J].IET Science Measurement Technology,2014,8(6):505-517.

[12] WANG G G,CHU H C E,MIRJALILI S.Three-dimensional path planning for UCAV using an improved bat algorithm[J].Aerospace Science & Technology,2016,49:231-238.

[13] AFRABANDPEY H,GHAFFARI M,MIRZAEI A,etal.A novel bat algorithm based on chaos for optimization tasks[C]//Iranian Conference on Intelligent Systems.USA:IEEE,2014:1-6.

[14] RAGHAVAN S,MARIMUTHU C,SARWESH P,etal.Bat algorithm for scheduling workflow applications in cloud[C]//International Conference on Electronic Design,Computer Networks & Automated Verification.USA:IEEE,2015:139-144.

[16] YOUNG G F,SCARDOVI L,CAVAGNA A,etal.Starling flock networks manage uncertainty in consensus at low cost[J].PloS Computational Biology,2013,9(1):e1002894.

[17] NETJINDA N,ACHALAKUL T,SIRINAOVAKUL B.Particle swarm optimization inspired by starling flock behavior[J].Applied Soft Computing,2015,35(C):411-422.

[18] XIE J,ZHOU Y,CHEN H.A novel bat algorithm based on differential operator and Lévy flights trajectory[J].Computational Intelligence & Neuroscience,2013(2013):453-812.

[19] 彭泓,丁玉成.基于遺傳交叉因子的蝙蝠算法的改進[J].激光雜志,2015(2):23-26.

[20] 劉金琨.先進PID控制MATLAB仿真[M].北京:電子工業出版社,2004.

AnImprovedBatAlgorithmBasedonStarlingFlockBehavior

HUFei,SUNZi-qiang

(KeyLaboratoryofAdvancedChemicalProcessControlandOptimizationTechnology,MinistryofEducation,EastChinaUniversityofScienceandTechnology,Shanghai200237,China)

Bat algorithm (BA) is a new metaheuristic algorithm.However,the standard BA has some shortcomings,e.g.,low convergence precision and easily relapsing into the local optima.In this work,by introducing the collective behavior of the starling group into BA algorithm,the searching range of the standard BA algorithm can be effectively improved.Besides,a linear decreasing weight is introduced to balance the global search and the local search.Simulation results from Benchmark functions show that the improved algorithm can effectively avoid the local optimum and attain higher convergence precision.

bat algorithm (BA); starling group behavior; weight; local optima

1006-3080(2017)04-0525-08

10.14135/j.cnki.1006-3080.2017.04.011

2016-11-01

胡 飛(1992-),男,安徽人,碩士生,研究方向為智能優化算法。 E-mail:xueshanfeihu1992@163.com

孫自強,E-mail:sunziqiang@ecust.edu.cn

TP301.6

A