類比中獲新知 應用中顯能力
——從高中數學類比法解題談起

☉湖南省隆回縣第一中學 王一帆

類比中獲新知 應用中顯能力
——從高中數學類比法解題談起

☉湖南省隆回縣第一中學 王一帆

在現行的高考制度下，高中數學學科具有十分重要的地位，學生的數學解題能力是數學教師和學生都關注的焦點；實踐表明，在高中數學各級各類質量檢測中，解題能力強的學生都能取得較高的分數；值得我們注意的是：數學思想方法的靈活運用是提升數學解題能力的重要保障；類比是一種數學思維方式與解題思想，在高中數學中主要涉及“概念、結構、次數、元數、方法”的類比，本文借助于典型案例的剖析，重點從“平面與空間、橢圓與雙曲線、低次與高次、少元與多元”等四個方面的類比進行探究，充分展現類比法在高中數學解題中的優越性與實效性，僅供參考，若有不當之處，敬請批評指正.

一、平面與空間問題的類比

在高中數學知識中，平面上涉及“點、線、面”，空間上涉及“線、面、體”，這些對應的元素，往往存在一定的數學類比關系，也是專家進行探究創新命題的素材；在幾何問題中，出現一種新的題型：“根據平面幾何的性質類比到空間問題之中，猜想、探究空間結構圖形中也滿足其性質特點”.

例1 已知O為△ABC的內切圓的圓心，AB=c，AC=b，BC=a，存在面積等量關系：S△OAB+S△OBC+S△OCA=S△ABC，則可得到△ABC的內切圓半徑；若將此平面三角形幾何性質類比至空間三棱錐問題中，即在三棱錐DABC中，S△ABC=SD，S△BCD=SA，S△CDA=SB，S△DAB=SC，試求：三棱錐D-ABC的內切球的半徑R的值.

剖析：平面三角形中，S△OAB+S△OBC+S△OCA=S△ABC，即，即；空間三棱錐中，令P為三棱錐的內切球的球心，存在體積關系V三棱錐P-ABC+V三棱錐P-CDA+V三棱錐P-BCD+V三棱錐P-DAB=V三棱錐D-ABC，即，即R=

點評：本題是根據平面幾何中存在的性質拓展類比至空間結構中，給學生探索、猜想的平臺，題中主要是根據“平面中的面積和”與“空間中的體積和”進行拓展類比，不僅考查學生類比聯想和空間想象的能力，更加注重學生邏輯推理和創新能力的考查與培養，符合新課改的主導思想.

二、橢圓與雙曲線問題的類比

在高中數學解析幾何問題中，橢圓和雙曲線是考查的重點之一，兩者之間存在一定的聯系與區別，若能搞清兩者之間的區別和聯系，有助于提升解決此類問題的效率.

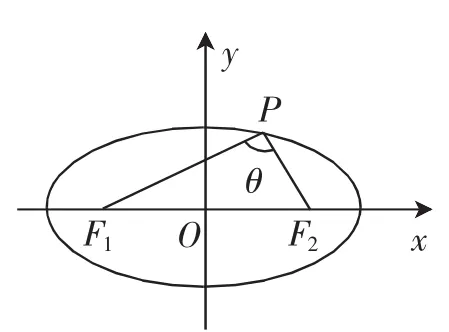
圖1

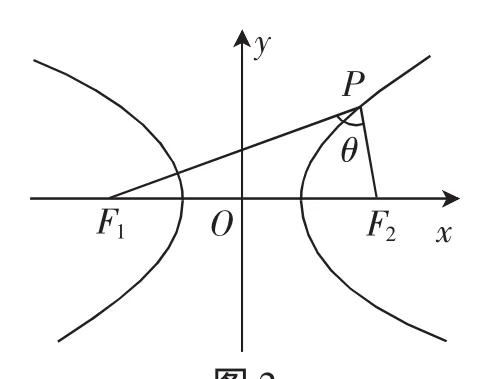
圖2

剖析：根據題意，構建如圖2所示雙曲線，令∠F1PF2=θ，|PF1|=m，|PF2|=n，則存在m-n=2a，4c2=m2+n2-2mncosθ，則，則可得到雙曲線焦點三角形面積的計算公式為

點評：本題主要探究橢圓和雙曲線的焦點三角形面積問題，橢圓中與雙曲線中兩個表達式結構十分相似，充分說明圓錐曲線中橢圓與雙曲線的本質規律的一致性，本題側重于計算橢圓與雙曲線焦點面積公式形式上的類比，有助于提升學生的邏輯推理能力.

三、低次與高次問題的類比

在高中數學的代數問題中，不等式的性質和不等式的應用是高考的重要內容之一，在含有字母參量的不等式中，若增加參量方根的次數可能會大大增加表達式的復雜性，但高中數學中的不等式問題含有一定的規律性，這是值得大家注意的地方.

例3 高中數學不等式章節中存在這樣一個性質：“兩個正數a、b的算術均值的平方小于等于其平方的算術平均值”，即且a=b時不等式中等號成立），其證明過程為，即可證明上述不等式性質成立；若增加參量的次數為3時，請根據不等式特征進行類比，寫出猜想的結論并加以證明.

剖析：根據參量次數是2時的特征，比較容易猜想次數為3時不等式性質表示形式為R+且a=b時不等式中等號成立），則

點評：本題中含有正參量的不等式性質直接源于課本中，多數學生十分熟悉，題設部分展示其證明過程，要求學生根據結構特征進行類比，推廣兩個參量的次數，可以得出結構相似的新結論，題中已經證明了次數為3時的正確性，對于心有余力的學生而言，這里可以進一步拓展次數增加4、5、…時，得出的新結論是否正確，并加以邏輯證明.

四、少元與多元問題的類比

不等式問題是高考的必考內容，不等式的考查形式呈現多樣化，不等式證明題是考查的重要形式之一，常規不等式題型中參量的元數通常是保持不變的，若增加參量的元數則難度加大，對學生的理解運用能力要求高.

剖析：根據題設呈現的不等式中三元對應三個具有“特色”分式形式，若由3個元數增加至4、5、6、…、n個元數時，不等式形式變為.此不等式證明如下：當n=3時，根據題設信息可知成立，假設n=k（k≥3）時，不等式成立，則當n=k+1時，存在不等式成立，則當n≥3時，類比猜想的不等式成立.

點評：本題是基于不等式問題，由三個字母參量的大小關系，得出“特殊”的分式不等式關系，再由三元拓展至多元，猜想得出新的不等式形式，采用數學歸納法對猜想內容進行證明與驗證，側重于考查學生拓展思維、猜想推理能力，在完成題目的一系列過程中體會類比思想方法在處理高中數學問題中的優越性和獨特性，同時激發學生探索新知的欲望.

總之，數學思想方法是解決高中數學問題的重要途徑，類比思想方法在解題中的有效運用有助于提升學生數學解題能力，讓學生在聯想、類比、拓展中不斷提升發現問題、提出問題、解決問題的能力，讓學生親身經歷數學知識、數學能力和數學素養“點→線→面→體”的逐步升華過程，感悟類比數學思想方法的“獨特”魅力.F