分類例談多元函數最值問題求解策略

☉浙江省寧波市北侖中學 范東暉

分類例談多元函數最值問題求解策略

☉浙江省寧波市北侖中學 范東暉

多元函數是高等數學中的重要概念之一，隨著新課改的推進，多元函數的值域與最值問題在自主招生、高考和各類數學競賽中也常有涉及.本文就常見的多元函數最值問題的求解策略加以梳理，供參考.

一、整體換元法

整體換元就是將數學問題中某一式子看成一個整體，然后用一個所謂的”元”去代替它，再用替換了的變量根據條件去構造成新的數學關系，這樣通過替換不僅可以實現數學問題的簡單化，而且使得與已知條件的聯系更為直觀.

例1 已知實數a，b滿足a2-ab+b2=3，求a2+ab+b2的最小值和最大值.

解析：將a2-ab+b2=3代入，得a2+ab+b2=（3+ab）+ab=3+2ab，下面只要求出ab的最值即可.由a2-ab+b2=3，得a2+2ab+b2=3+3ab，所以ab≥-1，當且僅當|a|=|b|=1，ab＜0時等號成立；再由a2-ab+b2=3，得a2-2ab+b2=3-ab，所以ab≤3，當且僅當a=b時取等號.于是-1≤ab≤3.

因此，a2+ab+b2的最小值是1，最大值是9.

評注：根據結論與條件中數學式子的結構特點，將條件整體代入結論表達式，盡管不能消元，但可化簡所求的結論.

例2 （2015年浙江省高考題）設x，y為實數，若4x2+xy+y2=1，則2x+y的最大值是_______.

解析：令2x+y=t，則y=-2x+t，代入已知條件，并化簡得6x2-3tx+t2-1=0.因為x為實數，所以由Δ=9t2-24（t2-1）≥0，得，所以2x+y的最大值是

評注：本題將要求的結論2x+y整體換元，代入已知條件，將問題轉化為“方程有解需要滿足的條件”來求解，這也是一種通性通法.

例3 已知x，y，z∈R+，且.求證：

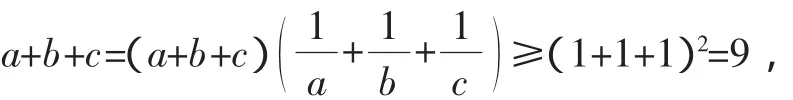
即a+b+c≥9.

二、配方法

當所給出的多元函數表達式的結構具有二次關系時，可考慮配方法來解決.

例4 （2014年浙江省競賽題）設a，b為實數，函數f（x）=ax+b滿足：對任意x∈［0，1］，有|f（x）|≤1，則ab的最大值為__________.

解析：易知a=f（1）-f（0），b=f（0），則ab=f（0）·［f（1）-

例5（2007年浙江省競賽題）設f（x，y，z）=sin2（x-y）+sin2（y-z）+sin2（z-x），x，y，z∈R，求f（x，y，z）的最大值.

評注：本題給出的式子的結構關系，利用基本不等式并不奏效，根據式中項與項之間的次數關系，我們選擇了配方法.

三、不等式法

利用基本不等式（均值不等式）和柯西不等式等求解最值問題.

1.利用基本不等式

故a3b2c≤27×4.

當且僅當a=3，b=2，c=1時，等號成立.

評注：本題應用了三元均值不等式來求多元函數的最值，但要注意應用條件“一正二定三相等”.

例7 （2015年全國數學聯賽題）若實數a，b，c滿足2a+4b=2c，4a+2b=4c，求c的最小值.

解析：將2a，2b，2c分別記為x，y，z，則x，y，z＞0.

由條件知，x+y2=z，x2+y=z2，

故z2-y=x2=（z-y2）2=z2-2y2z+y4.

由于c=log2z，故c的最小值為

評注：本題先用換元法將已知化簡，先求z=2c的最小值，進而求得c的最小值，同時要特別注意等號取得的條件.

2.利用柯西不等式

例8（2013年浙江省競賽題）設二次函數f（x）=ax2+（2b+1）x-a-2（a，b∈R，a≠0）在［3，4］上至少有一個零點，求a2+b2的最小值.

解析：由已知得，設t為二次函數在［3，4］上的零點，則有at2+（2b+1）t-a-2=0，變形為（2-t）2=［a（t2-1）+2bt］2≤（a2+b2）［（t2-1）2+4t2］=（a2+b2）（1+t2）2.

四、數形結合法

當我們所要求的多元函數的結構式與我們學過的一些公式（如兩點間距離公式、斜率公式、點到直線的距離公式、定比分點坐標公式等）的結構類似時，可考慮用數形結合的思想方法.

上題例8也可用數形結合法求解，把等式看成關于的直線方程：（x2-1）a+2xb+x-2=0，利用直線上一點（a，b）到原點的距離大于原點到直線的距離，即，接下來的解法同例8.

例9 已知實數a，b，c，d滿足（b+a2-3lna）2+（c-d+2）2=0，則（a-c）2+（b-d）2最小值是________.

解析：由已知可得b=-a2+3lna，d=c+2.（a，b），（c，d）可視為平面上的兩點坐標，則問題等價于求直線l：y=x+2上的點與函數y=-x2+3lnx的圖像上的點距離的平方的最小值.

由圖像易知，與直線l平行且與曲線y=-x2+3lnx相切的直線l0與直線l之間的距離的平方，即為所求最小值.

設切點（x0，y0），則由知，解得x0=1，所以切點為（1，-1），切線方程為y=x-2.

所以（a-c）2+（b-d）2的最小值為

評注：本題有4個參數，又夾雜著對數運算，比較難于找到問題的本質.采用數形結合的思想，把隱含的條件顯露出來，使看似一籌莫展的問題柳暗花明.

五、利用函數的單調性

先將多元函數轉化為一元函數，然后利用函數的單調性來確定最值.

例10設0≤x≤π，0≤y≤1.試求函數f（x，y）=（2y-1）sinx+（1-y）sin（1-y）x的最小值.

解析：由題意易知，對一切0≤x≤π，有sinx≥0，sin（1-y）x≥0.

，有tanx＞x＞sinx，

且sin（x+δ）=sinx·cosδ+cosx·sinδ≤sinx+δcosx.

則

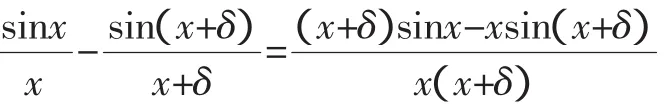
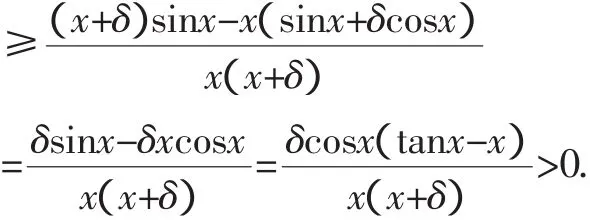
又因為0＜（1-y）x≤x≤π，

注意到（1-y）2=1-2y+y2≥1-2y＞0，

故（2y-1）sinx+（1-y）sin（1-y）x≥0，即f（x，y）≥0.

當y=0時，等號成立.

綜上，當x=0或y=0時，f（x，y）min=0.

六、賦特殊值法

有些競賽題直接解答有難度，不妨“退后一步”，從特殊出發，先探索出結論，再證一般性.

設x-2=cosθ（θ∈［0，π］），則

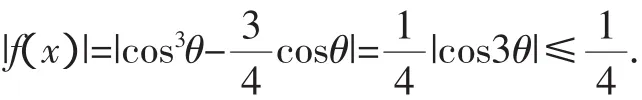
設g（x）=x3-ax2-bx-c，在區間［1，3］上，關于x=2對稱地取值

則

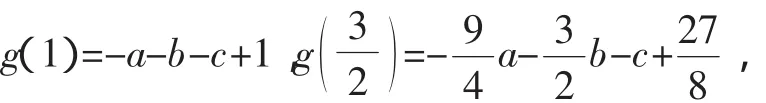
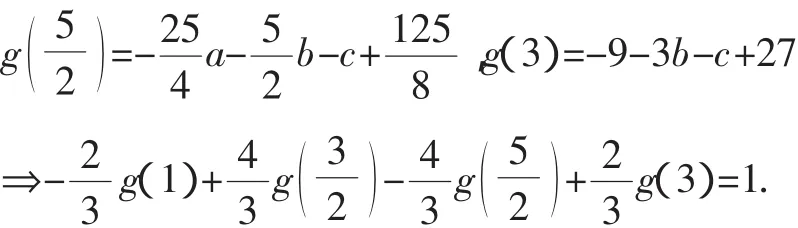
七、逐步調整法

例12 （北大自主招生題）已知a1+a2+a3=b1+b2+b3，a1a2+a2a3+a3a1=b1b2+b2b3+b3b1，若min（a1，a2，a3）≤min（b1，b2，b3）.

求證：max（a1，a2，a3）≤max（b1，b2，b3）.

證明：不妨設a1≥a2≥a3，b1≥b2≥b3，條件為：a3≤b3，

要證：a1≤b1.

由假設可知α≥β.

若α=β，則a1+a2=b1+b2，a1a2=b1b2，從一元二次方程根的角度可知，a1=b1.

若α＞β，因為a1a2+a2a3+a3a1=b1b2+b2b3+b3b1，所以

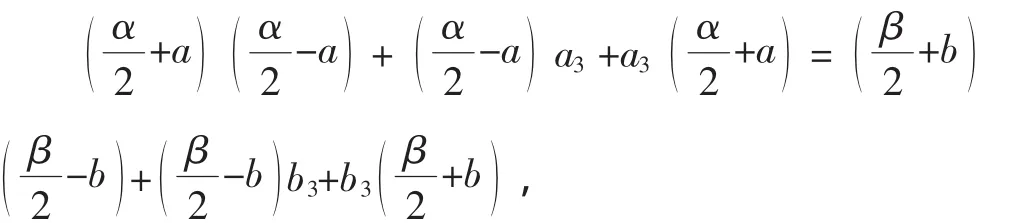
評注：本題采用分析法、換元法解決，利用式子的輪換對稱，假定字母的大小順序，從而產生分析法的思路.

最后指出，求解多元函數的最值問題，除了上述方法外，還有減元法、判別式法、分類討論法等，有時還需要多種方法的綜合運用.由于篇幅所限，這里不再一一舉例.