合理利用波利亞解題模型于解題教學

☉江蘇省錫東高級中學 葉 琳

合理利用波利亞解題模型于解題教學

☉江蘇省錫東高級中學 葉 琳

數學教學的重要任務是提高數學解題能力，學生解題能力的強弱很大程度上決定了數學教學質量的高低，因此提高學生解題能力這一任務應該貫穿于教學始終，它是一項長期復雜的系統工程.筆者結合備課組的教學模式，嘗試將波利亞的解題表具體化到可操作的步驟：讀題分析、提取組合、解題反思，并付諸于教學實踐，提高學生的解題能力.

波利亞的數學解題思想表現在解題表上：“第一，你必須弄清問題.第二，擬定計劃，找出已知數據與未知量之間的聯系.第三，實現你的計劃.第四，回顧檢查所得到的解.”它站在系統的高度給出了求解問題一般的步驟，在教學中我們從“讀題分析—有效提取—探索—解題反思”幾個步驟來訓練提高學生的解題能力.

一、生成合理的問題表征，引導學生分析

審題就是弄清問題，了解題意的過程，也是對問題進行表征的過程.解題教學的關鍵是指導幫助學生恰當地進行問題表征，尋找解題突破口，可以從以下幾個方面著手：①要將題目轉化為數學題目，比如實際問題（像應用題），要從題目中大量的文字語言描述轉化為數學語言描述出來.②列出題目中所給出的條件和要求，條件包括題目中給出的數據、等量關系、函數的模型等，還包括已有的公式、原理等；要求是指題目的問題，需要達到的目標.③搜索縮小條件和要求的范圍.在明確條件和問題后，結合已有的認知結構，確定判斷題目條件和問題中所涉及的知識點，可以用什么方法或者技能來解決.

案例（一）學生的讀題審題訓練

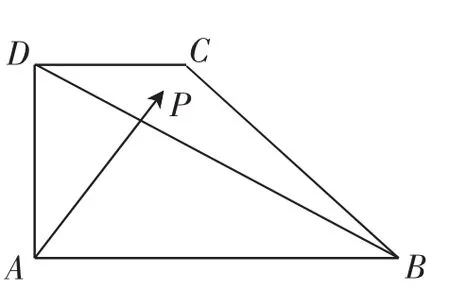
圖1

例1 如圖1，在直角梯形ABCD中，AB⊥AD，AD=DC=1，AB=3，動點P在△BCD內運動（含邊界），設，則α+β的取值范圍是_________.

讀題分析：（1）本題目本身就是數學語言闡述的題目，故不需要將其轉化為數學問題.

（2）條件有5個：“直角梯形ABCD”，“AB⊥AD”，“AD=DC=1，AB=3”，“P在△BCD內運動（含邊界）”，“；問題：求“α+β”的取值范圍.

（3）在明確條件和問題之后，開始判斷它們的范圍，“點P在△BCD內運動”，即點P的范圍在三角形內，可能要用到線性規劃來解決.

在實際教學過程中，我要求學生在讀題時養成把題目條件圈出來的習慣，考試或者解題時很多學生讀題很馬虎，讀題時一目十行，題目還沒看完就下筆去做，結果不是條件漏看了就是看錯了，導致解題錯誤.讀題時圈出條件，視覺感知變得強烈起來，第二遍讀題或者審題時可以關注圈出來的條件，減少審題馬虎導致的錯誤.

在教學實踐中筆者發現有些學生在讀題階段出現以下問題：①數學專有名詞理解困難.如求導數的極值點，學生不知道極值點是什么意思；再如利用“二分法”求方程的近似解，有的學生都不知道二分法是什么.②問題結構不清楚，信息識別能力低.有的學生對題目的表述不清楚，不能形成完整的問題空間，或者只知道問題的總體結構，但是不知道條件和問題分別是什么.

這是高三一輪復習“基本不等式”中的一道填空題，當時難倒了很多同學，有的同學讀題時就卡住了，不理解h的含義，它表示什么都不清楚，有的同學想到了本題是關于a，b的二元變量問題，可能要用到基本不等式，但是不知道條件是什么.這些都是因為學生受到數學語言的影響，不能正確地理解數學符號及模型與它們所表述的問題中的量之間的關系.

學生解題的能力與學生對問題的熟悉程度有關，這取決于他所具有的知識基礎和相關的解題經驗，如果他能夠用先前的知識合理地表征當前的問題，或者在以往的經驗中發現一個類似的問題，那么解決問題的可能性就比較大了.

二、有效提取組合，擬定解題方案

探索解題的途徑擬定解題方案是解題中最重要也是最困難的環節，可能這個環節它用時最多，而且在實施方案過程中發現它是錯誤的或者太繁，那么又要重新擬定新的解題方案.最為關鍵的是在每次探索過程失敗了，又要重新回到審題階段，找出失敗原因所在，重新提取組合，擬定方案.在整個解題過程中審題與擬定解題方案是緊密相連難以分開的，即審題中需要擬定方案，擬定方案中需要進一步審題.

在嘗試利用波利亞解題模式解題時，學生嘗試這樣的解題步驟：①讀題的同時圈條件，將文字轉化為數學語言，列出條件和問題；②讀題以后，你馬上想起的數學知識有哪些？你從已知、題設能想到什么，從結論中考慮需要什么信息，這兩者如何產生火花？

后面的思考有幾條常見的解題途徑（按順序）：

途徑1：“問題直接可以用定義、公式、定理求解”，把握題目的信息后，通過對問題表征的觀察，直接可以用相關的公式、定理、公理解決問題，或者從中挖掘符號、圖形、數量等信息，找到解題思路的突破口.

途徑2：在腦海里尋找相同的或者類似的題目，化新問題為已知問題.進入審題環節后，能否找出與新問題相關的問題或者題目類型，或者是相類似的問題，這里的相似可以是題目背景的相似，也可以是問題的闡述相似，或者是隱含的模型相似抑或問題的解法相似.因此掌握基本題型是有必要的，只有掌握了一些典型例題，在解決新問題時才容易找到化歸的方向.研究表明，學生類比聯想問題識別能力對學生的解題有很大的影響，可能會影響學生的解題速度，影響尋找策略和實施策略環節.

途徑3：多步化歸，改變表述方法.數學知識的特點之一是相互之間有著廣泛的聯系，面對復雜難題時已有的認知結構找不到相應的或者類似的模型，這時可以利用等價條件代換題設或者結論，嘗試去重新構造問題，組織問題，轉化為一個可能相關的問題或者熟悉的問題，再進行解題.在讀題分析的過程中，筆者讓學生說出解題過程中遇到困惑的地方，在思考過程中哪里出現了思路中斷或思路受阻，受到阻礙的原因是什么.解題結束后老師和學生一起分析、回顧解題中零星的想法和凌亂的解題思路，揭示解題的盲點，尋找繞過障礙的道路，找到出路.

案例（二）一次作業講評課片斷

在實施這樣的解題步驟的過程中，班級學生由不習慣到慢慢適應，在課堂教學中思維也漸漸活躍起來，一次的習題講評課讓我至今記憶猶新！實錄如下：

如圖2放置的邊長為1的正方形ABCD的頂點A，D分別在x軸，y軸正半軸上（含原點）滑動，則的最大值是_____________.

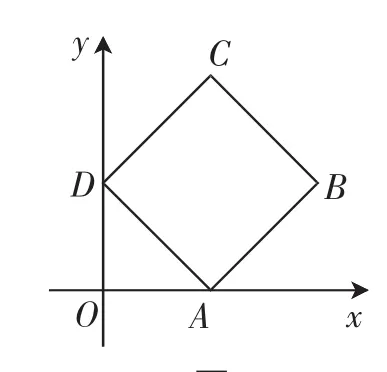
x A B C D O y

筆者在呈現出題目后，找學生起來讀題，學生分析完條件后給出了自己的思路：“老師我用平面向量基本定理做的由得到，其中α是與的夾角，故得到最大值為2.

筆者：很好，小Z同學從結論出發利用向量基本定理來處理這個問題，過程嚴謹，表述規范，是同學們學習的榜樣！

話音剛落，教室里討論聲響起來，男生小H站起來：“老師她的解法煩瑣了，我是用平面幾何做的，不要太省力哦.”

這樣的百家爭鳴的場景正是筆者需要的.

筆者：“真的嗎？你說說你是怎么做的？”

小H：“過B，C分別作x軸，y軸的垂線交并于M，N兩點，設AO=a，OD=b可以證明△AOD，△BAM，△BAM全等，所以OD=AM=CN，OA=DN=BM，設B（a+b，a），C（b，a+b），所以b（a+b）+a（a+b）=a2+b2+2ab，又最大值是2.

圖3

此時小M舉手示意：“老師，我是用矩陣變換做的！”

“矩陣變換也可以做？”不少同學露出驚訝的表情，（矩陣變換是附加里面的內容）.筆者也拿不準思路究竟對不對，就讓學生繼續往下說，設A（a，0），D（0，b），則可以看成繞A點順時針旋轉90°，求得B的坐標后，再同理求C的坐標，最后用數量積的坐標表示求得答案.下面不由自主地響起了掌聲.

課后筆者感慨頗多，如果我們的課堂都能像這節課一樣，各種解法百花齊放，每個學生都會在這節課學到很多，在教學活動中老師充分展示學生的思維過程，培養學生的創造精神和探索精神，當然教師的引領十分重要，對于學生易混淆的問題，要通過變式問題不斷強化，不斷練習，讓學生來領悟其中的解題奧妙，學會從多角度思考問題的方法.

三、適時解題回顧與反思，溫故而知新

波利亞說：“想要從解題中得到最大的收獲，應當深入理解如何解題的，思考是否還有更簡單的解題方法？如何克服障礙？本問題中是否隱含重要的思想方法等等.”現在很多學生迫于升學的壓力，整天在做大量的試卷中度過，但多數學生對解題過程的認識仍處于感性階段，解題追求數量的積累，以為數學多做題，能力就能提高，但是解題量的積累沒有促使質的轉變，最關鍵的是他們少了反思、回顧的過程，沒有反思就沒有總結就談不上提高.

筆者對班里數學較好的學生做了一次訪談，訪談中發現數學好的同學做完題目后，很多也是把題目丟到一旁，去找別的事做，很少去回顧過程.在一開始提出回顧反思這個話題時很多同學不知道怎么反思，筆者引導學生解題結束首先回顧解本題用到哪些知識，什么解題方法，其次一定要回顧本題的解題方法是什么，解題過程中走了哪些彎路，在哪里遇到了什么困惑，如何處理的等等.

回顧不光是回顧解題成功的經驗，更要反思解題失敗的教訓，找出犯錯的根源，每個學生都有過這樣的體驗——遇到難題時自己百思不得其解，而同伴或者老師稍加指點便想到了解題思路，而且解法不是很難.其實數學問題的解決往往在一個“思維點”上，這個思維點一旦突破，問題自然迎刃而解.通過解題反思可以梳理解題過程，突破自己的解題障礙，久而久之，就可以總結出帶有規律性的經驗，可以是解題策略，解題元認知知識等等，它們都是今后解題的經驗指南.