數學解題，不妨“無中生有”

郭建華

江蘇省南京市教育科學研究所 (210001) 劉權華江蘇省南京市第二十九中學 (210036)

數學解題，不妨“無中生有”

郭建華

江蘇省南京市教育科學研究所 (210001) 劉權華江蘇省南京市第二十九中學 (210036)

如果把解題比作打仗，那么解題者的“兵力”就是數學基礎知識，解題者的“兵器”就是數學基本思想方法，而調動數學基礎知識、運用數學基本思想方法的數學解題策略就是“兵法”.“無中生有”是三十六計中第七種計策.其意思就是制造假相欺騙敵人，但又不是弄假到底，而是巧妙地由假變真，由虛變實，以假相掩蓋真相，造成敵人的錯覺.無中生有，這個“無”指的就是“假”，是“虛”.這個“有”指的是“真”，是“實”.無中生有就是真真假假，虛虛實實，真中有假，假中有真，虛實互變.

在數學解題中，有時看似“無”，其實是“有”，關鍵是要有一雙“慧眼”.它對我數學解題的啟示是：在解決某些問題時，要根據該問題的背景、結構特征，通過觀察、比較、聯想，恰當地構造出某個數學模型.所謂構造法，就是根據題設條件和結論的特殊性，構造出一些新的數學形式，并借助它認識與解決原問題的一種思想方法．應用好構造思想解題的關鍵有二：一是要有明確的方向，即為什么目的而構造；二是弄清條件的本質特點和背景，以便重新進行邏輯組合．它的特點是：創造性使用已知條件，創造性地應用數學知識、數學模型等.下面結合例題，談談此法在數學解題中的運用.

1.充分地挖掘條件

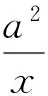
分析:此題若是將其中的一個變量借助等式用另一個變量表示，再行運算，未嘗不可，但是難度可想而知，若是充分地使用條件中的“1”，再利用書寫規則(當一個式的系數是1或-1時，“1”通常省略不寫)“無中生有”，立即就“柳暗花明”.

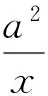
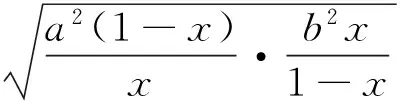
點評:但若是仔細觀察，便會發現左邊兩個式子的分母有以下的關系，x+(1-x)=1，就可以使用無中生“1”的方法簡便地予以證明了.本題中看似“無”，其實是“有”.關鍵是要充分的利用條件，挖掘條件，生出這個“有”來.

2.必要地巧用規則

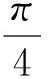
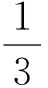
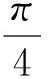
(2)sin2α+sin2α+cos2α=sin2α+sin2α+cos2α-sin2α=2sinαcosα+cos2α

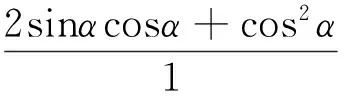
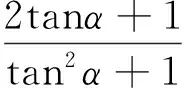
點評:在推導sin2α，cos2α和tan2α中用tanα表示的萬能公式時，皆可以運用此法，效果確是恰到好處.

3.深刻地借用定義

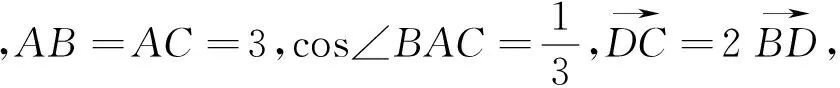
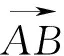
兩組治療前血液流變學指標比較，差異無統計學意義（P＞0.05），治療后，觀察組血沉、纖維蛋白原、紅細胞壓積、全血黏度、血漿黏度分別為（12.08±1.79）mm/h、（3.19±0.33）g/L、（0.43±0.05）L/L、（4.65±0.37）、（1.61±0.19），均低于對照組，差異有統計學意義（P＜0.05），見表1。

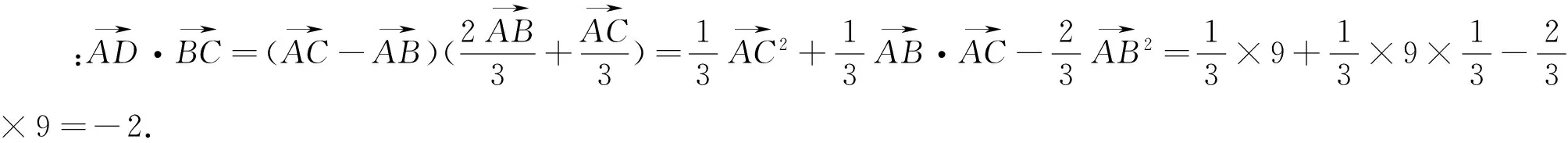
點評:此題，關鍵之處是對向量根據定義，巧妙拆分，無中生“A”，使得問題迅速解決.在定比分點的向量表示中，此法極為常用.此法就是利用充分向量減法的定義.此題中，由于AB=AC,故也可以由圖，無中生“系”，通過建立直角坐標系，轉化為對應的坐標，再用“代數法”求解，也很簡單.

4.創造地利用模型

例4 6位身高不同的同學排成兩排三列，若每列后面的同學均比他前面的同學高，則不同的排法有多少種？

點評:概率論是研究隨機現象的一門數學分支，它既有獨特的概念和方法，又與其它科學分支有著密切的聯系，因此在解答有關數學問題時，如能根據題設條件構建概率模型，可使這些數學問題簡潔巧妙地解決.

5.巧妙地使用規定

例5 4個0怎樣能算出24？

解析:在階乘(n!=1×2×3×…(n-1)×n，0!=1)的教學中，筆者帶領同學們做游戲——算24點，“算24點”就是給一組數，通過一些數學運算(加、減、乘、除、乘方、括號)，使其結果等于24，每個數字都要用上，并且只能用一遍.比如給一組數2,3,4,6.一般有這樣幾種算法.法1：2×6+3×4=24；法2：(3-2)×4×6=24；法3：(6-3)×2×4=24.等.運算的范圍一般在有理數范圍內，最常見的方法就是構造24的因數3,8,4,6,2,12.

通過簡單幾個題目在他們小有成就而沾沾自喜的時候，我出了一道題：4個0怎樣能算出24？足夠的時間，激烈的討論，學生們可謂絞盡腦汁，最后筆者給出了答案：(0！+0！+0！+0！)！=24，學生紛紛嘆為觀止，接著筆者點撥到：這就是“無中生有”，學生一下子群情激昂，雷鳴般的掌聲經久不息，學習數學的情緒一下子就被調動起來.這似乎上升到“文化”的境界，這是我們多么渴望追求的一種高境界啊！然而，第二天一大早，有一個學生跑到筆者的辦公室，急不可耐地告訴筆者，“老師，老師，我又有一種辦法，“00∶00”就是24點呀……”內容如此的切合，學生如此的執著，一切都是那樣的妙不可言.這樣的故事，學生一生可能也難以忘懷.這樣的過程似乎上升到一種更高的只可意會的境界.

6.巧妙地使用方程

例6 在平面直角坐標系xOy中，已知圓O1，圓O2均與x軸相切且圓心O1，O2與原點O共線，O1，O2兩點的橫坐標之積為6，設圓O1與圓O2相交于P，Q兩點，直線l：2x-y-8=0，則點P與直線l上任意一點M之間的距離的最小值為_________.

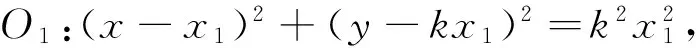
點評:根據已知條件與所求式子的特征，探尋問題的結構特征和數量關系，挖掘潛在已知與未知因素，從而聯想有關的方程(或方程組)，利用方程理論求解，使問題在新的關系下轉化，將陌生問題熟悉化，復雜問題簡單化.

“無中生有”中的“有”，可以是數，可以是點，可以是圖形，可以是坐標系，還可以是模型.這種方法，其實就是我們常說的“構造法”中的一種，構造法解題是一種創造性地思維過程，具有較大的靈活性和技巧性.在運用過程中，我們要仔細分析題目的結構特點，善于聯想，應有目的，有意識地進行構造，始終“盯住”要“求”的目標.通過構造特殊數字、特殊規定(如0!=1)、特殊模型等將“未知軌道”中的問題轉化為“常見可解的軌道”上來.