探析一道解析幾何題的求解策略
虞 懿
浙江省金華市第六中學 (321000)
探析一道解析幾何題的求解策略
虞 懿
浙江省金華市第六中學 (321000)
解析幾何的核心方法是用代數的方法研究圖形的幾何量(性質),核心思想是“數形結合”.2017年高考浙江卷第21題,保持了浙江卷背景熟悉、入口寬泛、解法多樣的一貫風格,細細品讀深感底蘊純厚,緊扣解析幾何的思想精髓.本文從解決解析幾何問題的核心思想出發,著重探究本題第(Ⅱ)問的求解策略.

圖1
一、試題展示

(Ⅰ)求直線AP斜率的取值范圍;
(Ⅱ)求|PA|·|PQ|的最大值.
品讀:本題以拋物線為載體,主要考查拋物線的幾何性質、直線與拋物線的位置關系、斜率與弦長等基礎知識,同時考查解析幾何的基本思想方法和綜合解題能力.設計新穎,構思巧妙,耐人尋味,令人賞心悅目,體現了“能力立意”的指導思想,凸顯了數學試題的選拔功能.
二、求解策略

(Ⅱ)策略1:選擇恰當形式,實現幾何量的代數表示
“幾何量的代數表示”是解決解幾問題的關鍵,在本題中的幾何量是“|PA|·|PQ|”,用什么樣的代數形式來表示這個幾何量?對于弦長問題,很自然地聯想到圓錐曲線的距離和弦長公式.而在解幾中描述弦長的代數形式就是點或斜率,由此可想到用點坐標或斜率來表示幾何量“|PA|·|PQ|”.
解法1:聯立直線AP與BQ的方程
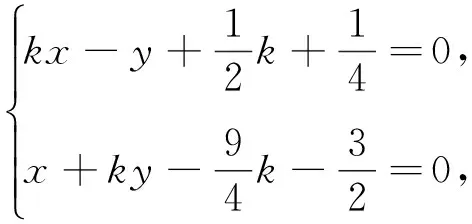
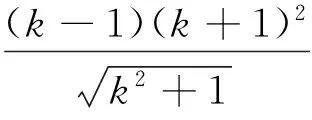
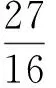
評析:聯立兩相交直線方程求出點Q的坐標,再根據兩點間的距離公式,以斜率為參變量來表示弦長,建立目標函數.



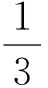

評析:涉及弦長的問題,應熟練地利用根與系數的關系,通過設而不求計算弦長,以求達到簡化運算的目的.
策略2:借助參數方程,實現幾何量的代數表示

評析:利用直線的參數方程中參數的幾何意義,避免了繁瑣的計算,使得方程的聯立簡便易得.
策略3:回歸向量知識本質,實現幾何量的代數表示
向量具有代數、幾何雙重身份,融數形于一體,是溝通代數和幾何的橋梁.它可以將幾何問題坐標化、數量化,因此它是解決解析幾何問題的重要工具.
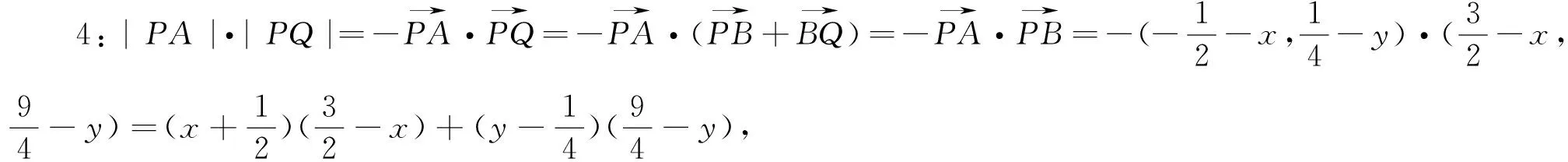
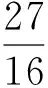
評析:本解法構建平面向量,利用數量積的定義求|PA|·|PQ|,簡潔明了.在探究解題思路時,要善于從不同的角度分析、挖掘它與其他知識的聯系,在平面解析幾何中有關長度、角度的計算及有關平行、三點共線、垂直等位置關系問題都可以用向量知識解決.
策略4:妙用極化恒等式,實現幾何量的代數表示



評析:極化恒等式的應用,由一般的直接運用到結合具體問題的巧用,需要學生恰當地運用轉化思想,注意化動為定,特別是要結合題中的隱性特征進行轉化處理,才能達到事半功倍的效果.
策略5:利用圓冪定理,實現幾何量的代數表示
圓冪定理是平面幾何中的一個定理,是相交弦定理、切割線定理及割線定理(切割線定理推論)的統一.例如,如果交點為P的兩條相交直線與圓O相交于A、B與C、D,則PA·PB=PC·PD.
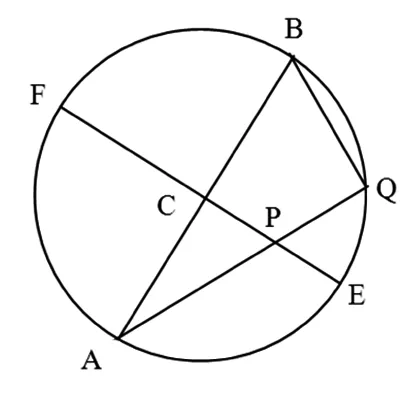
圖2



評析:巧妙利用圓冪定理進行轉化,得|PA|·|PQ|=R2-|PC|2,避開求點Q的坐標,從而大大簡化運算,并且后續化簡也比較方便.
三、探究感悟
解析幾何的核心方法是用代數的方法研究幾何問題,在解題過程中,首先要將文字信息、圖形條件進行轉換,通過代數語言描述幾何要素及其關系,將待求的幾何量表示成代數式,然后進行適當的代數運算得出代數結果,最后通過分析代數結果的幾何含義解決幾何問題.在這個過程中要經歷文字信息、圖形特征和符號語言之間的多重轉換,因此,我們必須重視對幾何量(關系)的深入研究,探究用何種代數形式能恰當表示題目中的幾何量(關系),同時有利于代數運算,從而形成正確的解題策略.

