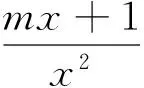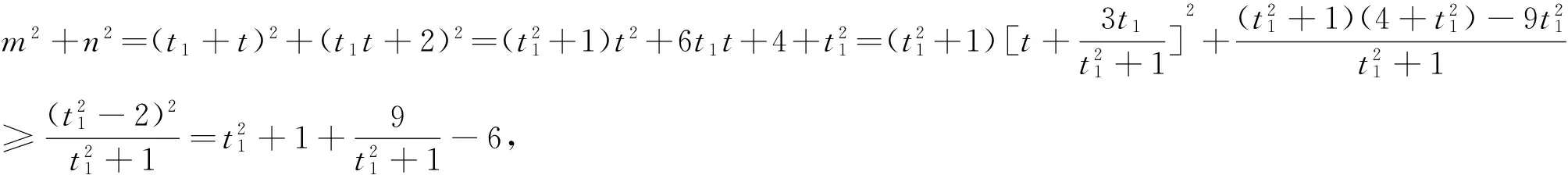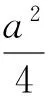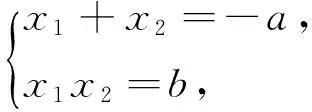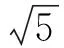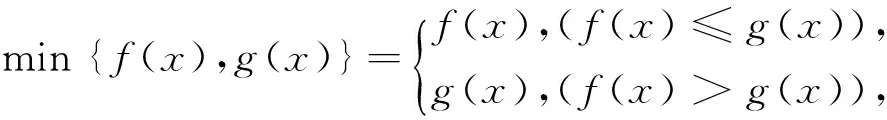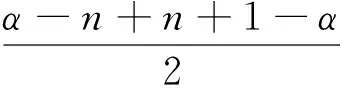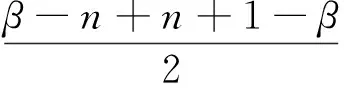利用函數零點式妙解一類函數題
嚴婷婷 陳少春
浙江省紹興魯迅中學 (312000)
利用函數零點式妙解一類函數題
嚴婷婷 陳少春
浙江省紹興魯迅中學 (312000)
函數是高中數學中一個非常重要的核心知識,二次函數作為眾多函數里的“明星”備受考試命題者的青睞.最近浙江的模考卷、競賽卷里頻頻出現一類函數問題,筆者發現如果用二次函數的零點式去處理,簡潔明了,事半功倍.
例1 (2017年浙江高中數學競賽題)設f(x)=x2+ax+b在[0,1]有兩個實數根,則a2-2b的取值范圍為_________.
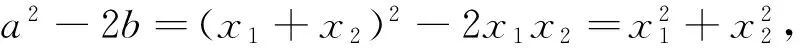
例2 (2014年浙江高中數學競賽題)已知b,c∈R,二次函數f(x)=x2+bx+c在(0,1)上與x軸有兩個不同的交點,求c2+(1+b)c的取值范圍.
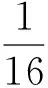
例3 (2017年浙江高考調測卷17題)已知函數f(x)=x2+ax+b在(0,1)有兩個零點,3a+b的取值范圍是_________.
解:設f(x)=x2+ax+b的兩個零點為x1,x2,則0 例4 (2017年浙江模擬題)已知函數f(x)=ax2+bx+c(a>0)在(0,1)有兩個零點,f(0)·f(1)是正整數,求實數a的最小值. 例7 (2015年浙江高考文數21題)設函數f(x)=x2+ax+b(a,b∈R). (2)若函數f(x)在[-1,1]上存在零點,0≤b-2a≤1,求b的取值范圍. 解:(1)略; -3≤b<0. 例8 (2011年北大保送生試題)設p、q為實數,函數f(x)=x2+px+q,如果f(f(x))=0只有一個實數根,求證:p,q≥0. 解:由題意知,f(x)=0必有實數根,設f(x)=(x-x1)(x-x2),故f(f(x))=(f(x)-x1)(f(x)-x2).下面用反證法證明x1≤0,x2≤0.不妨設x1>0,則由二次函數f(x)=x2+px+q開口向上及f(x)=0有實根知,方程f(x)-x1=0有兩個不相等實根t1,t2,即f(x)-x1=(x-t1)(x-t2),所以f(f(x))=(f(x)-x1)(f(x)-x2)=(x-t1)(x-t2)(f(x)-x2)至少有兩個不相等的實根,與題設矛盾.從而p=-(x1+x2)≥0,q=x1x2≥0.