一道IMO試題的推廣

李汝雁 郭要紅

安徽師范大學數學計算機科學學院 (241000)

一道IMO試題的推廣

李汝雁 郭要紅

安徽師范大學數學計算機科學學院 (241000)

2014年第55屆IMO試題4如下：

題目點P和Q在銳角△ABC的邊BC上，滿足∠PAB=∠BCA，且∠CAQ=∠ABC，點M、N分別在直線AP、AQ上，使得P為AM的中點，且Q為AN的中點.證明：直線BM與CN的交點在△ABC的外接圓上.

文[1]刊登了試題的一個證明，本文用三角法給出該試題的一個推廣.

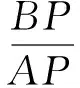
圖1

如圖1，設∠NCQ=α，∠MBP=β，直線NC與直線MB相交于T.則∠QNC=∠AQC-α=∠A-α,∠BMP=∠APB-β=∠A-β.

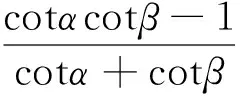
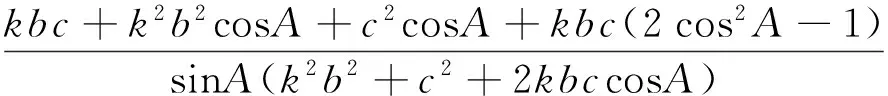
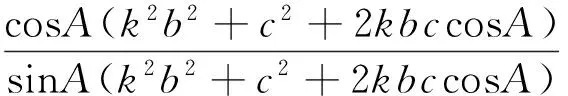
故α+β=A，所以∠BTC=180°-(α+β)=180°-∠A，即點T在△ABC的外接圓上.

當k=1時，即AP=PM時，AQ=QN，點P、Q分別為AM、AN的中點，本文定理即為試題，所以定理是試題的推廣.

[1]姚一雋.第55屆IMO試題解答[J].中等數學，2014(9)：20-24.