輔助線添加策略的探尋

[摘 要] 本文通過對平面幾何中“輔助線的添加”進行探討，提出“從定義模型中發現輔助線身影，在操作實驗中確定輔助線思路，從美學角度尋找輔助線蹤影，從平衡理論中尋找輔助線印跡，從大小格局中探尋輔助線蹤跡”五種策略.

[關鍵詞] 輔助線；策略；實驗；格局

在平面幾何教學中，輔助線的添加往往是學生幾何學習的“攔路虎”，對優等生來說，也常心有余悸，對中等生來說，更是噩夢一場. 許多學生都有這樣的體會：如果題目有輔助線做法的提示，那么問題就會較快得到解決，但如果沒有提示，往往會陷入束手無策之中. 一日，徒弟鄭巧斌老師（以下簡稱鄭）問我：“陳老師，學生在學習幾何時總是很怕做需要添加輔助線的題目，你有什么好的教學策略嗎？”這個問題在平面幾何教學中確實經常遇到，是一類最常見且迫切需要解決的問題. 雖然輔助線千變萬化，但也并非無跡可尋，于是我們有了如下討論.

從定義模型中發現輔助線身影

陳海烽（以下簡稱陳）：輔助線的添加確實是一個值得我們深入研究的問題，我們一起來梳理一下. 初中階段是從什么時候開始涉及需要添加輔助線的幾何題目的？

鄭：應該是從第五章“相交線與平行線”（人教版）就開始的吧！

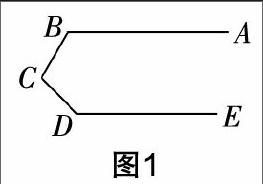
陳：很好，其實在這個章節中，一般老師會遇到如下這道題. 如圖1，已知AB∥DE，求證：∠ABC+∠BCD+∠CDE=360°.

鄭：對，這道題很典型，但是學生的掌握情況好像不好，如果知道要過點C添加一條輔助線，那么這道題就很簡單了.

陳：你認為學生為什么想不到添加輔助線呢？

鄭：對結論的把握不清晰. 如果知道兩個180°，那么就應該知道要添加輔助線了.

陳：你只講對了一部分. 其實在教學時需要我們有所“作為”的. 如何刻畫兩條直線平行，除了我們的外在感官外，還需要有一條直線輔助，才能將位置關系轉化為數量關系，這就需要一條截線. 我們現在看到AB∥DE，還看到了一條折線BCD，但這并不是截線，那么我們需要幫助，這個幫助就是我們做輔助線的“念頭”.

鄭：如果從這個思路或想法入手，就會有很多辦法.

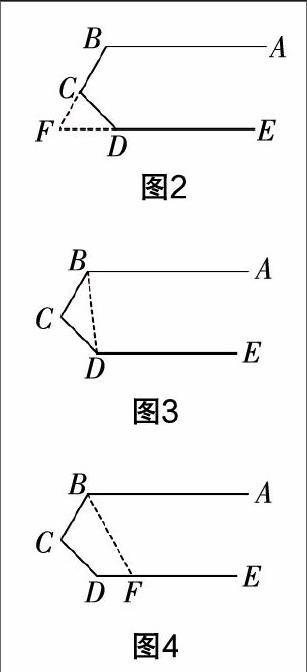
陳：是的，至少有如下策略（如圖2～4）. 當然，如果學生認為BC是一條截線，回到平行線的基本模型，這時就需要過點C作CF∥AB（或CF∥DE），圖5也就是你所說的方法，那么自然就水到渠成了.

鄭：是不是可以這樣理解，我們在講解定義或模型時要理清模型中的結構，這樣可以幫助學生理清模型特征，還原出模型. 《義務教育數學課程標準》修訂組組長史寧中說過：“模型的最初建立是基于觀察和想象的，而不是基于推理的；判斷模型正確與否的標準是基于經驗的，而不是基于理性的. ”比如平面直角坐標系中，我們經常添加垂直于兩軸的垂線段，這也是基于對坐標本質的理解吧.

陳：總結得很好. 比如我們看到有公共頂點的兩條相等線段，其實具備了旋轉的部分特征——頂點可以看作旋轉中心，兩條相等的線段可以看成是由其中一條線段經過旋轉而形成的. 這時我們可以考慮將圖形進行旋轉. 所以，希望我們老師在講解的時候可以幫助學生理清這個結構模型. 不少老師善于總結解幾何題的一些基本圖形，這些基本圖形就是題目的一個“器官”，教學時我們要多創設情境加以指認和識別，提高學生的審圖能力，進而提升他們的核心素養.

在操作實驗中確定輔助線思路

陳：我們再來看一道單元測試中的試題. 如圖6，在等腰三角形ABC中，AB=AC，∠A=20°，在邊AB上取一點D，使AD=BC，求∠BDC的度數.

鄭：這是競賽題呢，這是壓軸題！這道題我做過，學生肯定很少做出來，貌似要構造等邊三角形，但是如何想到要構造等邊三角形的呢？

陳：是的，這也是很多優等生也存在的疑問. 講解這道題時，我讓學生進行了數學實驗.

鄭：頭一回聽說數學實驗，說具體點.

陳：我讓學生量出∠BDC=30°，然后追問學生，如果∠BDC=30°，那么∠ACD應該為多少度？學生都回答10°，接著我再追問學生，在本圖中，如何才能得到有個10°的角？學生馬上想到作∠A的平分線. 我又繼續追問，這樣一來，我們能否找到一個和△ADC全等的圖形？需要多少度的角？學生回答需要有20°的角，這時讓學生自己探索，就有不少同學發現以BC為邊作等邊三角形后，就會出現一個含20°角的三角形，從而問題就容易解決了. 如圖7，以BC為邊作等邊三角形OBC，易證△ABO≌△ACO，接著證明△ACD≌△CAO，就可以得出答案了.

鄭：您這樣讓學生實驗操作，學生就很容易從這些條件中找到答案，而且學生經歷了操作確認的過程，能完成邏輯證明. 記得《義務教育數學課程標準》就指出：“學生應當有足夠的時間和空間經歷觀察、實驗、猜測、計算、推理驗證的過程. ”數學實驗正好契合新課程理念，有利于提升學生的核心素養.

陳：沒錯，我們在教學時要讓學生學會數學實驗，當然也包括思維實驗，我們現在最流行的數學軟件——幾何畫板也可以用來探尋作輔助線的思路. 在精確作圖的基礎上，借助最常用的三角板、量角器等數學學具，可以幫助我們發現一些靠譜的結論，這就等于把握了解題的方向，使我們的解題不至于像無頭蒼蠅. 這里要特別說明的是，對于一些較難的壓軸題，雖然題目中已經配上了圖形，但是學生看到的只是成品，并沒有看到這個圖形的生長過程，所以建議在教學時務必讓學生感受這個過程，讓學生知道這個圖形是如何生長出來的，同時通過這個過程，感悟圖形要素（或元素）之間的從屬關系，進而在確定圖形的過程中生長出作輔助線的念頭.

從美學角度尋找輔助線蹤影

陳：我們還可以從美學特征中尋找輔助線蹤影.

鄭：美指的是那些簡潔美、對稱美、和諧美、奇異美嗎？endprint

陳：是的，其中對稱美對我們添加輔助線幫助最大. 拿我們最常見的角平分線來說，通過它，我們能將這個角進行翻折，或者說角是一個軸對稱圖形，角平分線所在的直線就是它的對稱軸. 如果能從這個角度就可以找到解題思路.

鄭：比如下面這道題. 如圖8，AD平分∠BAC，∠B+∠C=180°，求證：DB=DC.

陳：這個題目很典型，如果學生知道角平分線是一條美學中心線，利用美學思想，可以有如下幾種作法（如圖9～11）.

鄭：從美學角度，相信學生能更好地理解輔助線作法的由來，也可以知道這三種輔助線作法本質上是一致的，對一題多解就更加容易接受了. 我覺得很多翻折、平移、旋轉其實也是一種廣義的對稱，也都具有美學的特征.

陳：沒錯. 教學時我們應該多從美學的角度闡釋數學知識，比如教學垂徑定理時，可以讓學生通過折疊圓的方法，充分利用其對稱美來研究問題，這樣，學生對定理的認識就會有新的高度. 再如，直線與圓的位置關系，也可以通過對稱美折疊圓的方法發現很多性質. 經過這樣的引導教學，學生更容易明白為什么要作弦心距這條輔助線，為什么見到切線要連半徑得到垂直.

從平衡理論中尋找輔助線印跡

陳：此外，我們還可以從平衡理論中找尋輔助線印跡. 比如我們常見的截長補短就是一種很好的平衡理論的應用. 如要證明“a=b+c”，常用的策略就是從a中分成兩段相加，即a=b1+c1，即先讓b=b1，然后證明c=c1，這樣，式子的兩邊就都是兩兩相加的結構，兩邊都平衡了，達到了證明的目的. 當然，我們也可以將“b+c”通過輔助線將其延長，補成一條線段a，從而完成證明，這是很明顯的應用之一. 學生明白了這些，就會更容易理解截長補短的本質. 當然，類似的還有如下試題. 如圖12，已知點E，F分別在正方形ABCD的邊BC，CD上，分別連接AE，AF和EF，若∠EAF=45°，試說明EF=BE+DF.

鄭：你的意思是∠EAF=45°占了∠DAB的一半，另外兩個角，即∠EAB和∠DAF的和也是45°，我們要將兩者拼在一起才能平衡，所以想到作輔助線，將圖形△ADF進行旋轉，是嗎？

陳：沒錯，這樣的話，學生的理解會更順一些.

鄭：是的，實際上，總有很多學生想將EF截成兩段，或者過點A作EF的垂線段. 如果能從平衡中入手，就不會再糾結了.

陳：對. 因此，在教學中，遇到線段或角的和、差、倍、分問題，要引導學生從結論出發，利用平衡理論原理，讓學生體會將結論逐步轉化的過程，即從不平衡的狀態通過恰當的輔助線達到平衡的狀態.

從大小格局中探尋輔助線蹤跡

陳：另外，我們還可以從大小格局中尋找輔助線蹤跡. 比如，我們看到一個有關中點的題目，我們會提醒學生展開聯想.

鄭：就是聯想倍長中線，三線合一，直角三角形中斜邊上的中線等于斜邊的一半，中位線定理等.

陳：說得好，譬如倍長中線，還有不少老師總結“倍長中線找倒8”，也就是找個“8”字形的結構，然后讓學生證明全等.

鄭：對呀，這有什么問題嗎？

陳：當然沒什么問題，但是我們可以引導學生從更大的格局來看待問題. 倍長中線后，除了兩個全等的三角形外，我們其實還可以看到一個平行四邊形，讓學生連接成平行四邊形后，需要通過全等獲得的條件可以直接從平行四邊形中獲取，解題的書寫長度更短.

鄭：學生老是用全等，看來可以再稍做改進. 我們在平面直角坐標系中，經常讓學生補成矩形或梯形，將三角形的問題看作是它們的一部分，是不是可以看作是這種策略的運用？

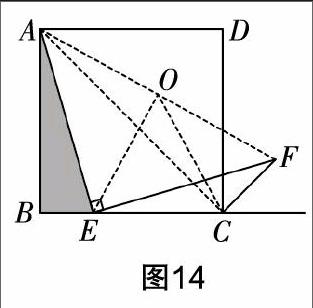
陳：是的. 當然，我們在教學時要注意對課本知識進行再探究. 比如下面這道題. 如圖13，四邊形ABCD是正方形，E為BC上一個動點，∠AEF=90°，且EF交正方形ABCD的外角平分線CF于點F，求證：AE=FE.

陳：這道題是我們在八年級下冊學習“正方形”后的一道課后習題，課本還給出了相應的提示. 我們在初三教學四點共圓的條件時再讓學生做這道題，發現了雙直角模型，存在的一個更大的格局是A，E，C，F四點共圓，于是添加如下輔助線證明更為快捷. 如圖14，連接AC，AF，取AF的中點O，連接OE，OC，則AO=EO=CO=FO. 所以A，E，C，F四點共圓. 所以∠AFE=∠ACE=45°. 所以△AEF是等腰直角三角形. 所以AE=FE.

鄭：哦，我知道了，比如將四邊形的問題轉化為三角形問題，再將一般三角形問題轉化為特殊的直角三角形問題，就是從小格局上入手. 若把斜三角形放在一個大矩形或一個平行四邊形中，就是從大格局上考慮. 教學時，我們要讓學生感悟事物之間是普遍聯系的這一哲理，讓學生知道一個圖形不是孤立的，可以前后關聯在一起，形成一個更加良好、系統的格局.

陳：是的，這樣的例子相當多，對學生來說也比較容易想到. 教學時，要提醒學生輔助線的功能就是將分散的條件集中起來，將隱含的條件顯現出來. 另外，作輔助線一般要遵循一個原則，即“不可貪，不可破”！其中“貪”的情況比較普遍，比如學生經常在作輔助線時說這條輔助線不僅能和誰垂直還要和誰相等，這顯然就是貪多了，再如本文開頭的第一道題，假如作平行線CF∥AB且CF∥DE，顯然不妥. “不可破”就是作輔助線時盡量不要破壞已知條件，不能通過輔助線得了一個條件，反而失去一個可用的條件，這樣反而得不償失了.

鄭：這個本質和原則今后我會加強滲透，總結你講的上述策略，我發現也很有美感. 一，從定義模型里尋找輔助線身影；二，從實驗操作上尋覓輔助線思路；三，從美學特征中發現輔助線蹤影；四，從平衡理論里尋找輔助線印跡；五，從大小格局中尋找輔助線蹤跡. 今后，在執教中引導學生通過解題慢慢領悟，就能不斷地提高他們的數學素養，那么學生對需要添加輔助線的題目就會更有信心.endprint