由遞推式求數列通項公式的四種常見類型研究

李曦霞

(昆明官渡區第二中學,云南 昆明 650041)

由遞推式求數列通項公式的四種常見類型研究

李曦霞

(昆明官渡區第二中學,云南 昆明 650041)

數列是高中數學的重要內容之一，而數列問題中出現最頻繁的要數是求數列通項公式.本文結合高中新課改教材(人教A版)及最新高考大綱要求，談一談由遞推式求數列通項公式的四種常見類型方法，利于培養學生的創造力、觀察力和思維能力，提高學生學習數學的興趣.

遞推式 數列 通項公式

數列是高中數學的重要內容之一，是連接初等數學與高等數學的橋梁，在歷年高考試題中占有一定的比例.而數列問題中出現最頻繁的要數是求數列通項公式.如何求數列的通項公式成為解決數列問題的關鍵.但是求數列通項往往靈活性較強，特別是由數列的遞推式找數列的通項公式，直接求解有時比較困難，而在一些綜合性比較強的數列問題中，求解過程往往方法不一，技法較強，給初學者在學習過程中帶來困惑.本文從這點出發，結合高中新課改教材(人教A版)及最新高考大綱要求，談一談由遞推式求數列通項公式的四種常見類型，希望能對初學者有所幫助.

類型一形如an+1=an+f(n)

遞推式形如an+1=an+f(n)，可轉化為an+1-an=f(n)，與等差數列的遞推式相似，可仿照等差數列求通項公式的方法“累加法”來求其通項公式.

由an+1=an+f(n),

有an+1-an=f(n),

a2-a1=f(1),

a3-a2=f(2),

a4-a3=f(3),

…

an-an-1=f(n-1) (n≥2).

以上n-1個式子相加，

an-a1=f(1)+f(2)+f(3)+…+f(n-1),

類型二形如an+1=f(n)·an(f(n)≠0,an≠0)

以上n-1個式子相乘，

故an=a1f(1)f(2)f(3)…f(n-1) (n≥2).再對a1進行檢驗.

類型三形如an+1=pan+q的遞推式

當p=1時，數列為等差數列；當p≠0,q=0時，數列為等比數列.

當p≠1,p≠0,q≠0時，令an+1-λ=p(an-λ)，展開整理，

an+1=pan+(1-p)λ.

對比an+1=pan+q有(1-p)λ=q，

例1 已知數列an滿足：a1=1，an+1=pan+q，且a2=3，a4=15，求p,q的值及數列an的通項公式.

解得p=-3，q=6 或p=2，q=1.

由(2)中an+1=2an+1，有an+1+1=2(an+1)，所以an+1+1是以a1+1=2為首項，公比q=2的等比數列， 故an=2n-1.

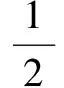
類型四形如an+1=pan+f(n) (p≠0)的遞推式

將上式兩邊同時除以pn+1，得

例2 數列an的前n項和為Sn，且滿足a1=1，an+1=2Sn+n2-n+1 (n≥1),求數列an的通項公式.

解由an+1=2Sn+n2-n+1, (1)

有an=2Sn-1+(n-1)2-(n-1)+1 (n≥2) (2).

(1)-(2)得：an+1-an=2an+2n-2 即an+1=3an+2n-2.

∴b2-b1=0,

…

以上n-1個式子相加，

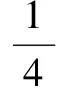
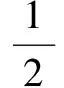
經檢驗此式對b1也成立,

由數列的遞推式求數列的通項公式，需要滲透多種數學思想方法，尤其轉化思想，類型三與類型四就是通過構造新數列，把不熟悉的數列轉化為熟悉的等差或等比數列或常見類型一或類型二，特別是即非等差數列，又非等比數列的求通項問題，除了采用不完全歸納法進行歸納、猜想，然后借助于數學歸納法予以證明，還可以通過構造新數列轉化為上述四種類型來處理，有助于初學者理解數列的概念以及數列與函數的關系，加強學生對知識的橫向聯系，促進學生對知識進一步掌握，同時有利于培養學生的創造力、觀察力和思維能力，提高學生學習數學的興趣.

[1]王朝銀.高中數學步步高大一輪復習講義[M]，哈爾濱：黑龍江教育出版社,2015.

[2]周貞雄.百試百樂專題考王高中版[M].長沙：湖南教育出版社，2005.

[責任編輯：楊惠民]

2017-07-01

李曦霞(1971-)，女，漢族，湖南人，學士，中學一級教師，從事高中數學教學.

G632

A

1008-0333(2017)28-0011-02