突破計數單位學習困難的教學思考

梁洪超

[摘 要]在平時的教學和聽課活動中發現，學生在學習整數、分數、小數的計數單位時都存在著較大的困難，而且大多數教師對計數單位的理解也存在偏差。通過深入挖掘教材對“10以內數的認識”中長方形背景框的使用，依托計數單位來銜接整數、小數和分數體系之間的聯系，讓學生在計數單位的拓展和累加中完成數的認識的學習，為學生的計算打下堅實的基礎。

[關鍵詞]計數單位；10以內的數；主體地位

[中圖分類號] G623.5 [文獻標識碼] A [文章編號] 1007-9068（2017）32-0020-03

【重要地位】

數的認識的核心是對“位值原則”的理解，而“位值原則”可以理解為計數單位和進位法則的高度統一。正是計數單位的出現，才使人們實現了用0～9這10個數字來表示無窮無盡的數的可能。因此，從這個角度來看，計數單位是組成數的基石，在數的認識中有著不可替代的地位。

新課改后，計算教學的總課時數和習題數量都較以前大幅度減少，學生的計算能力也隨之減弱。要改變這一現狀，首先要求學生對算理有一定的理解，而理解算理又必須對計數單位有一定的理解，理解計數單位則要從數的認識的學習中實現。

目前，計數單位的教學到底處于一個什么樣的狀態呢？

【現象掃視】

現象一：學生學習小數的計數單位時感覺很難。

2010年春，我有幸參與了縣小數研修班“小數的意義”的“同課異構，一課多上”的研討活動，三位上課教師的教學都別具匠心，各有千秋，然而在教學小數的計數單位時，卻碰到了相同的困難：即使教師費盡九牛二虎之力對學生加以引導，學生卻總是似懂非懂，學得十分吃力。在課后的交流討論中，與會教師也都覺得對此沒有有效的應對之法。

后來我在“千課萬人”的聽課活動中，看到唐彩斌老師在執教“小數的意義”時，從學生熟知的整數引入，以教師的不同身高為載體，層層引入、環環相扣，不禁令人眼前一亮。然而，他在教學小數計數單位時，也遇到了同樣的問題。

現象二：在調查學生掌握計數單位的情況中發現，正確率不足五成。

隨后我對本校五年級七個班，學號末位數為0或5的學生進行了一次問卷調查，結果發現學生對計數單位的掌握情況不容樂觀。

如，題目：整數的計數單位有（ ）、（ ）、（ ）、（ ）……與它們相對應的數位分別是（ ）、（ ）、（ ）、（ ）……小數的計數單位有（ ）、（ ）、（ ）（ ）……與它們相對應的數位分別是（ ）、（ ）、（ ）、（ ）……

學生解答該題的正確率僅為53.90%，其中有近六成的學生是因為分不清數位和計數單位的概念而出錯。

后來我對四年級的學生進行訪談，聽說過“計數單位”這一詞的學生竟不足兩成。大多數學生認為計數單位和數位很難區分，學習計數單位也沒有什么用處。由此可見，學習計數單位的困難并不僅存在于“小數的意義”這一節課中，學生對整數和分數的計數單位的學習也存在同樣的困難。

【成因分析】

1.對教材缺乏深入的研讀

對于學生學習計數單位困難這個現象，諸多教師都認為造成這些的原因是教材中計數單位概念出現的次數太少。分析整套人教版教材，在1～12冊教材中，出現“計數單位”這一完整概念的總共只有6次：第一、二次分別出現在四年級下冊第3頁“億以內數的認識”和第20頁“十進制計數法”的整數數位順序表中；第三、四次分別出現在四年級下冊第51頁“小數的意義”和第52頁“小數的讀法和寫法”的小數數位順序表中；第五、六次分別出現在五年級下冊第62頁“分數的意義”和第64頁練習十一的第8題中。如此重要的內容，在教材中的“出鏡率”顯然太低。尤其是對整數的教學，直到教學了“個、十、百、千、萬、十萬、百萬、千萬、億”這些計數單位，在整數的認識教學即將結束時，教材中才第一次出現“計數單位”這一完整概念。

2.過分強調生活情境，缺少計數單位的適時抽象

課改后，越來越多的教師認識到數學情境生活化的重要作用和意義，然而數學情境過分生活化，卻導致許多數學知識抽象程度不夠，為學生日后學習更深層次的數學知識留下隱患。如，四年級下冊“小數的加法和減法”中的“5.72+1.3”，對于為什么要把7和3相加而不是2和3相加，有的學生是根據元、角、分的情境來理解，認為角和角對應相加，分和分對應相加；有的學生是根據長度單位來理解，認為分米和分米對應相加，厘米和厘米對應相加；很少有學生能從“計數單位”的角度上去理解算理。雖然前兩者的理解都對，但無論從數學知識的抽象程度，還是對學習后續知識的影響上看，教師都應該將學生向后者的方向上引導。其中，對后者理解上的缺失也正好反映了學生在學習“計數單位”中存在的問題。

3.教師對計數單位的理解也十分模糊

在與許多教師的訪談中發現，大家對計數單位的認知和理解存在著很大的分歧。有些教師認為：5個5個地數，5就是計數單位；8個8個地數，8就是計數單位；一位小數最大的計數單位應該是0.5，因為2個0.5正好可以湊成一個更大的計數單位。有些教師認為，只有以10個、100個、1000個等進行數數的時候才能將其叫作計數單位，而5個5個地數時，5就不能稱之為計數單位。我專門就這一問題向杭州新思維培訓中心的姜榮富老師請教，才清楚：無論是幾個幾個地數，都不能稱之為計數單位，只能叫作按群計數，只有在計數和計算時才會有計數單位的概念。真正的計數單位只有1，其他的計數單位都是人為創造的。也就是說，只有在位值制出現后才有計數單位一說。

綜上，學生出現上述問題的原因包括：傳統教學中只重視計數單位的知識講授，使得學生對計數單位的學習只停留在數的組成和分解之中，沒有經歷計數單位從量變到質變的逐步累加過程，忽略了新計數單位學習的必要性，以及理解和體會它的重要作用。因此，教學的改進可以從以下這幾方面入手。endprint

【改進方略】

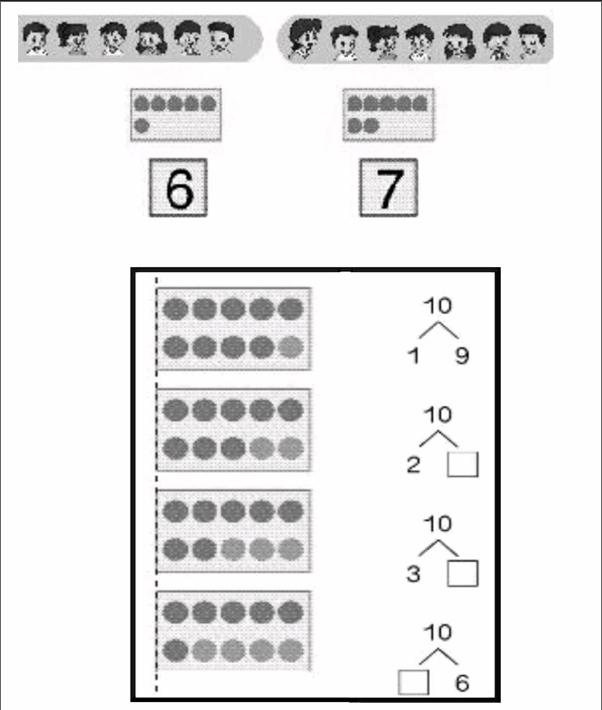
1.加強教材的深入發掘，重視長方形背景框的使用

深入整理和研讀教材中“10以內數的認識”的內容，不難發現，從“5以內數的認識”開始，到“10的認識”，教材中都配了長方形背景框中的點子圖，這顯然是對10作為計數單位的有意滲透。教師在教學時若能用好這個背景框，不但可以促進學生理解10作為計數單位的意義，對學生學習20以內數的進位加法和退位減法，并能夠用湊整思想進行簡算都大有幫助。

眾所周知，20以內數的進位加法是一年級計算教學的難點，因此很多教師在教學“7加幾的進位加法”時，常常會讓學生背誦“看到7想到3，把幾分成3和幾……”的計算口訣，然而不少學困生對“看到7一定要想到3”表示難以理解，這是因為學生對“10”作為“計數單位”的理解不夠深刻造成的。如果教師能在教學“6和7的認識”時，利用好點子圖的背景框（滲透計數單位“10”）讓學生思考“把這個長方形框擺滿，還能再擺幾個點子？你是怎么想的？”；在教學“10以內數的認識”時，對于10的分解和組成，結合點子圖讓學生畫一畫、想一想、做一做……學生就能獲得對計數單位“10”更多的直觀體驗，給學習進位加法的算理打好基礎。

2.在“10的認識”中突破“10”的局限性，讓“10”成為新數認知的新起點

在教學“10的認識”時，“10”應該是本課教學的終點，大多數教師在教學中都會安排學生進行“把10根小棒捆成1捆，把10顆珠子串成1串”等操作活動，以此來加深學生對新的計數單位的理解。而這樣的操作大都是“被操作”，學生并沒有真正理解教師要求操作的目的。從“10作為計數單位”的角度來思考，“10”不該成為“10的認識”的教學終點，應該是學生認識新數的一個新起點。因為，從理論上講，學生學了“10的認識”后再去數數時，應該就可以數到10個“十”。

因此，在以上操作活動的基礎上，教師應帶領學生再向前多走一步，讓計數單位真正變得有用。

【教學片段】一年級上冊“10的認識”

師（多媒體出示散亂的小方塊，引導學生從1數到10；多媒體出示很多個散亂的小方塊（100個），鋪滿整個屏幕）：共有幾個小方塊？

生1：太多了，數不清楚。

師：通過電腦操作，我們把原來分散的每10個“一”組合成了現在的1個1個的“十”。

師：現在我們再來數一數。

生2：一個“10”、兩個“10”、三個“10”……一共有十個“10”。

師（小結）：“1個1個”散亂地數太費時了，我們可以把它們稍作整理，變成“10個10個”地數，就可以把原來數不清楚的小方塊數得很清楚了。

在學習每一個新的計數單位時，都讓學生經歷這一幕，學生對計數單位的作用就能有更加深刻的體會了。

3.在小數和分數體系的認識和拓展中，讓計數單位先行

張奠宙教授在2011年《小學數學教師》的第4期中就明確闡述了“小數有自己的概念系統，不能也不必依賴于對分數的理解”“小數的本質是位值計數法的拓展，而不是十分之幾的表述”等觀點。

【教學片段】小數的意義

師（出示一把沒有刻度的尺子）：如果我用自然數1來表示這把尺子的長度，你覺得教室門的高大約可以用什么數字來表示？黑板的長呢？

生1：2、4。

師：這支毛筆的長度呢？能用幾個1來表示？

生2：毛筆的長度還不到1。

師：也就是說現在用1作為計數單位太大了，那該怎么辦？

生3：我們需要創造一個比1更小的計數單位。

師：有道理。那么我們把1平均分成幾個小的計數單位比較好呢？

生4：平均分成10個比較好，因為整數也是滿十進一。

師：你很會思考，整數是滿十進一，這里就可以是“一分為十”。

師（多媒體演示：把一把尺子平均分成10份） ：這樣我們就創造了一個比1更小的計數單位——0.1（十分之一），那接下來（取下自制尺子中的0.1，邊演示邊講解）我們就可以0.1為單位進行計數和測量物品了。

師：數數看1里面一共分成了幾個0.1呢？（板書：1里面有10個0.1）那么，現在毛筆的長度是幾個0.1呢？3個0.1可以怎么表示？

生5：0.3。

師：空白部分有幾個0.1，可以用什么分數來表示？

生6：7個0.7，表示為■。

師：沒錯，有了0.1這個計數單位以后，就可以方便我們數數了。我們一起來數一數。（教師帶領學生一起從0.1數到1）

師：這個0.1是把1平均分成10份，每一份其實就是分數里的十分之一，所以我們也可以十分之一、十分之一地數。0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9、1.0、1.1……

【設計意圖：兩次數數，第一次以0.1為單位數，第二次以十分之一為單位數，從而幫助學生理解小數都是由0.1累加而成的，十分之幾是由十分之一累加而成的，進一步強化了學生對計數單位的體驗，有利于增強學生對小數意義的理解，與華羅庚先生“數，數也！”的見解相吻合。】

其實，無論整數、分數、小數，還是十進制、二進制、八進制等，都只是計數單位和進位法則上存在區別，在這些內容中，整數的十進制是學生學習課時最長，生活體驗最為豐富的內容。因此，教師要抓住計數單位的改變這一主線，先拓展計數單位，再帶領學生數計數單位的個數，最大限度地借助學生整數學習中的經驗，依托計數單位讓學生對小學階段各數系的認識實現無縫對接，以此為后續的相關計數教學打好基礎。

[ 參 考 文 獻 ]

[1] 中華人民共和國教育部.全日制義務教育數學課程標準（修訂稿）[S]. 北京：北京師范大學出版社，2010.

[2] 張奠宙. 談小數教學[J]. 小學數學教師，2011（4）.

[3] 吳振亞. 關于計數單位的教學思考[J]. 小學教育教學，2011（1）.

（責編 童 夏）endprint