基于拉格朗日插值的光纖陀螺時延補償方法

張 峰，黃繼勛，王頌邦

（北京航天時代光電科技有限公司，北京 100094）

基于拉格朗日插值的光纖陀螺時延補償方法

張 峰，黃繼勛，王頌邦

（北京航天時代光電科技有限公司，北京 100094）

針對光纖陀螺存在時延環節而影響了光纖慣組的導航位置精度的問題，從陀螺儀原理出發，分析光纖陀螺儀時延產生的機理以及不同方向陀螺儀時延特性與導航位置精度之間的關系。在此基礎上，提出了基于拉格朗日插值的時延補償方法，通過拉格朗日插值運算得到當前時刻的對準信息，從而實現了三個方向的陀螺儀輸出的時間配準。通過仿真和多自由度導航試驗驗證，證明了該方法的正確性和有效性，該方法易于實現，通過補償導航位置精度提高了21%。

光纖陀螺儀；定位精度；拉格朗日插值；多自由度導航

光纖陀螺是一種基于 Sagnac效應的角速度敏感器[1]，具有精度高、體積小、重量輕等優點，由光纖陀螺為核心的光纖慣組產品已經廣泛地應用在飛機、艦船、火箭等載體。由閉環光纖陀螺儀原理可知，陀螺儀輸出特性等效為一階慣性環節和純時延環節的乘積，并且不同陀螺儀的延遲時間各不相同。由于延遲特性的存在勢必對組成的光纖慣組的精度造成影響。文獻[1-2]研究了數字閉環光纖陀螺動態特性測試，通過動態特性的數字測試方法辨識帶寬和時延參數；文獻[3]研究了光纖陀螺時滯環節的實時補償技術，采用最小二乘法對光纖陀螺的測量輸出進行預測用以補償其時滯環節，但并沒有分析陀螺儀的時延特性對導航精度的影響；文獻[4]研究了加速度計時延與導航速度誤差之間的關系，但未涉及到光纖陀螺儀的時延與導航誤差關系；文獻[5]研究了激光陀螺捷聯慣導系統中整周期采樣的修正研究，提出了線性外推補償方法，重點分析了時延對姿態誤差的影響，但沒有分析對導航位置精度的影響；文獻[6]將拉格朗日差值方法用于信號延遲重構方面，該方法的理論可為光纖慣組的時延補償提供了一定的指導意義，但該方法并未分析時延產生的影響以及針對光纖慣組如何具體實現。

本文從陀螺儀原理出發，分析了時延產生的原因和對導航位置精度的影響，建立了基于拉格朗日插值方法的時延補償方法，開展了仿真分析和試驗驗證，證明了方法的有效性，能夠有效地補償陀螺儀時延造成的導航位置誤差。

1 時延特性分析及導航精度影響

1.1 光纖陀螺時延特性分析

光纖陀螺主要由光源、探測器等光路和 A/D、D/A、FPGA等電路組成，其中，光路的帶寬較高，通常能達到幾兆赫茲以上，幾乎不存在時延，而電路部分由于需要對信息的采集，解算調制解調，因此電路部分的時延較為明顯。以下對陀螺儀的各個部分時延情況進行詳細分析：

1）Sagnac效應時延

由光纖陀螺原理可知，其敏感的相位誤差ΔRΦ可以表示為

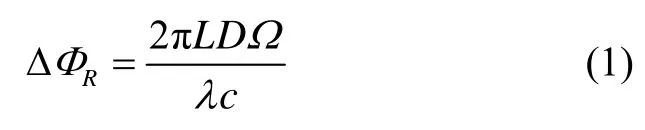
其中，λ表示光源的波長，c為光在真空中的速度，D表示光纖環直徑，L表示光纖總長度。可以看出，轉速Ω與相位差ΔRΦ成正比關系，且是瞬時產生，可以認為原理上無延遲產生。

2）處理電路時延

閉環光纖陀螺儀在電路設計上需要增加閉環反饋控制環節，處理周期為光纖環的渡越時間τ，即：

其中，n為光纖的折射率，n= 1.456。考慮到閉環處理中方波調制、A/D采樣延遲及積分電路的計算延遲，通常處理電路延遲在1～2個渡越周期，該時間通常在μs量級。

3）軟件處理時延

在光纖陀螺中電路中，通常采用FPGA作為核心控制部件，主要完成A/D和D/A數據處理和時序控制，如圖1所示。

圖1 硬件接口圖Fig.1 Hardware interface

FPGA算法處理時間較長，通常為ms量級，是導致光纖陀螺時延的主要因素。

4）數據傳輸時延

數據傳輸時間主要是由發送數據的波特率和數據字節長度決定，通常也在 ms級。若陀螺按照輸出波特率為460 800 bps，傳輸的6個字節數據，則傳輸的時延為0.1 ms左右。

通過以上分析，光纖陀螺儀總的時延在ms量級，不同參數的陀螺儀(光纖環長度L、A/D和D/A運算速度)的時延不同，但即使相同參數的陀螺儀，由于使用的器件個體性能差異如晶振溫漂參數不一致性，陀螺儀時延也不相同，因此，陀螺儀具體的延遲時間需要標定試驗獲得。圖2是某型光纖慣組(三個軸陀螺儀參數一致)時延參數。

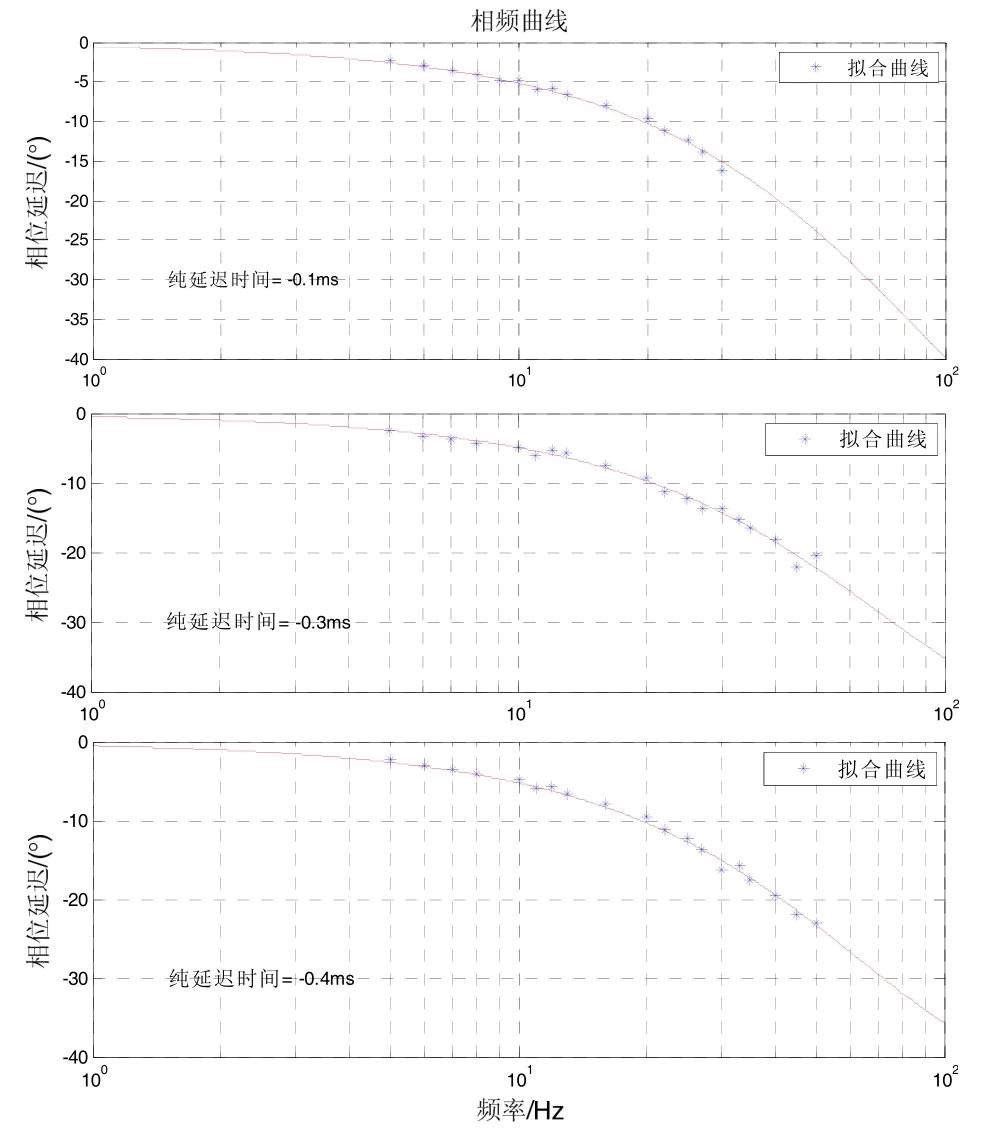
圖2 三軸陀螺儀時延測試結果Fig.2 Results of three-axis gyro delay time

通過測試得到該光纖慣組三只陀螺儀的時延結果如表1所示。

表1 三軸陀螺儀的延遲時間Tab.1 Delay time of three gyros

1.2 陀螺時延對導航位置精度的影響

在不考慮高度方向的影響，慣導位置隨時間的誤差方程如式(3)所示：

其中：δL、δλ分別表示緯度誤差和經度誤差；L、λ表示緯度和經度；εe、εn、εu分別表示東、北和天向陀螺儀的漂移；ωie表示地球自轉角速度；▽e、▽n分別表示東向和北向加速度計的漂移；ωs表示舒拉頻率。

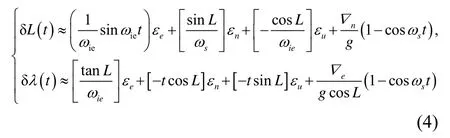
從公式(4)可知：東向陀螺儀漂移εe引起的緯度方向的誤差是振蕩的，引起的經度方向的誤差是常值誤差；北向陀螺儀漂移εn引起的緯度方向的誤差是常值的，引起經度方向的誤差為線性累積的，系數為cosL；天向陀螺儀漂移εu引起的緯度方向的誤差是常值誤差，引起的經度方向的誤差是線性累積的，系數為sinL。以下考慮了不同方向的陀螺儀的時延對導航位置精度的影響：

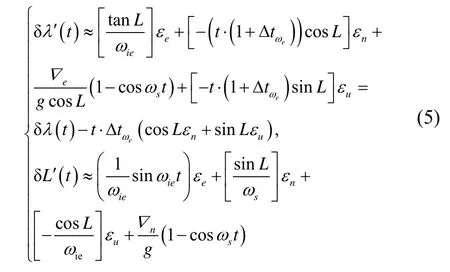
其中：δλ′和δL′表示由時延產生的經度和緯度方向的誤差。由公式(5)可知，經度方向的誤差將比無時延情況下發散的更快，與時延的時間成線性增長。而由緯度誤差方程可知，此時對緯度的影響相對較小。

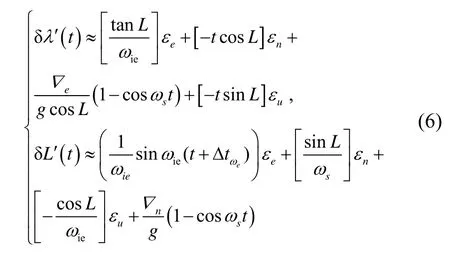
從公式(6)可以看出，北向陀螺儀時延主要引起了緯度方向的振蕩周期，而對經度方向影響較小。

2 基于拉格朗日插值方法的時延補償技術

設三個方向的陀螺儀(gx、gy、gz)在時間軸上的輸出序列分別為如圖3所示，圖中Tk-1、Tk表示導航計算機采樣時刻，時間間隔為h，陀螺儀輸出周期為以X陀螺輸出gx為例，在tk-1、tk和tk+1時刻對應的輸出為則運用拉格朗日三點插值法計算出tk時刻的測量值為

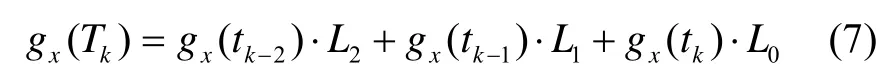
其中：

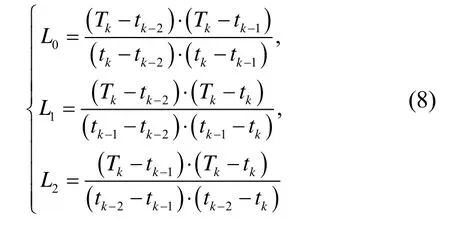
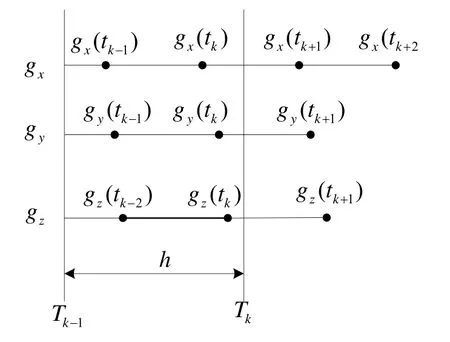
圖3 三軸陀螺時延輸出示意圖Fig.3 Schematic diagram of three-axis gyro delay time

根據公式(8)得到X陀螺在Tk時刻的輸出值。設光纖慣組采樣周期為 5 ms，三只陀螺延遲時間分別為-0.1 ms、-0.3 ms、-0.4 ms。三只陀螺儀在50 ms時刻對準時，拉格朗日插值估算結果如圖4紅線值部分。

當時延未補償，且三個軸向陀螺儀在第50 ms時刻的輸出為分別為-0.023 (°)/s、0.007 (°)/s、0.002 (°)/s，采用拉格朗日插值方法對時延進行補償時，對三個軸陀螺儀輸出時間配準得到第 50 ms時刻的輸出分別為-0.0225 (°)/s、0.005 (°)/s、0.0015 (°)/s。采用拉格朗日插值方法可以簡單地實現三個軸的陀螺儀輸出在時間軸上對齊，完成了信息融合的時間匹配。

圖4 三軸陀螺儀時間配準圖Fig.4 Temporal registration of three-axis gyros

3 仿真分析與試驗驗證

3.1 仿真分析

設緯度L=40.0689°，陀螺儀的零偏穩定為 0.01(°)/h，加速度計的零偏穩定性為 100 μg，為按照東向陀螺儀和北向陀螺儀分別時延遲0.1 ms和0.5 ms的狀態作靜態導航的仿真。由式(5)和式(6)可得，當時延時，經度方向將多產生的100 m的誤差；當時延Δtωe=0.5 ms時，經度方向將多產生的500 m的誤差。仿真曲線如圖5(a)～5(d)所示。

由圖5(a)～5(d)可知，光纖慣組不同方向陀螺儀時延特性的理論計算與仿真分析結果相吻合，證明了理論分析的正確性。

圖5(a) 東向陀螺儀時延0.1ms引起的導航誤差Fig.5(a) Navigation error caused by 0.1ms delay time of east gyros

圖5(b) 東向陀螺儀時延0.5 ms引起的導航誤差Fig.5(b) Navigation error caused by 0.5ms delay time of east gyros

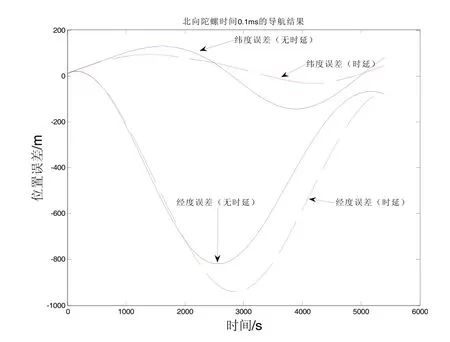
圖5(c) 北向陀螺儀時延0.1ms引起的導航誤差Fig.5(c) Navigation error caused by 0.1ms delay time of north gyros

圖5(d) 北向陀螺儀時延0.5ms引起的導航誤差Fig.5(d) Navigation error caused by 0.5ms delay time of north gyros

3.2 試驗驗證

為了驗證時延補償方法對導航位置精度影響，開展了光纖慣組多自由度導航試驗。采用自對準方式，對準時間為60 s，導航時間為600 s，分別按照未時延補償和時延補償的兩種方式進行。緯度誤差和經度誤差輸出結果如圖6所示，輸出結果如表2所示，多自由度導航試驗圖如圖7所示。

從表2試驗結果分析可以看出，對陀螺儀的時延補償提高了三軸陀螺儀動態環境輸出的同步性，導航位置誤差由原來的651.7490 m減小至515.0498 m，提高了近21%，尤其是緯度誤差改善較為明顯。

表2 補償前后導航位置誤差Tab.2 Position errors before and after compensation

圖6(a) 北向誤差輸出曲線Fig.6(a) Output curve of latitude error

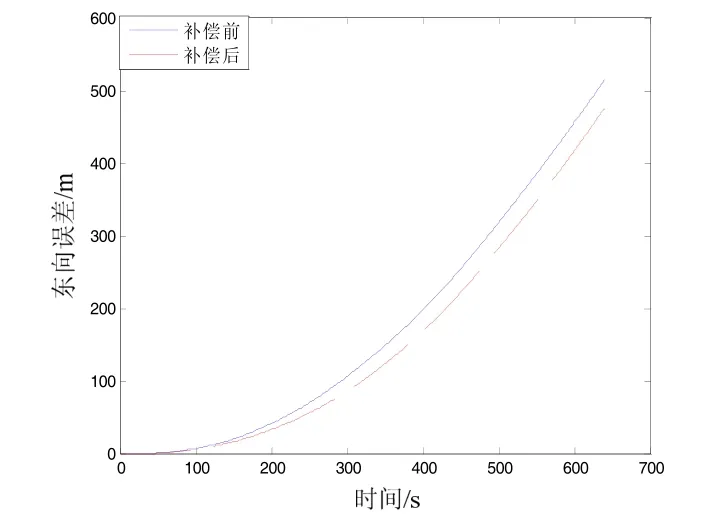
圖6(b) 東向誤差輸出曲線Fig.6(b) Output curve of longitude error

圖7 多自由度導航試驗圖Fig.7 Six-degree of freedom navigation

另外由慣導原理可知，若光纖慣組三個軸存在連續的角運動，則在導航算法中會因為時延的問題導致角運動的不可交換性誤差變大且不斷累積，最終導致嚴重的姿態解算誤差。對三軸陀螺儀輸出的時延補償也能有效地提高慣組的姿態精度。

由于拉格朗日算法較為簡單，實際為多項式乘法運算，計算簡單，實時性強。

4 結 論

本文從光纖陀螺儀原理出發，分析了時延產生的原因，定量分析了光纖慣組不同方向陀螺儀時延對導航精度的影響。針對方向陀螺儀時延的問題，提出了采用拉格朗日插值的時延補償方法，開展了試驗驗證，從試驗結果可以看出該方法能夠有效提高光纖慣組動態環境下的導航位置和姿態精度，相比未補償導航精度提高了21%。

（References）：

[1]王巍.干涉型光纖陀螺技術[M].北京: 中國宇航出版社,2010: 281-287.

[2]李星善, 馬珣, 袁慧錚, 等.光纖陀螺角速率延遲特性分析與測試[J].導航位置與授時, 2016, 3(1): 69-72.Li X S, Ma X, Yuan H Z, et al.Analysis and test for angular rate delay characteristics of fiber optic gyroscopes[J].Navigation Positioning & Timing, 2016, 3(1): 69-72.

[3]毛耀, 馬佳光, 包啟亮.光纖陀螺時滯環節的實時補償技術[J].光電工程, 2009(2), 36(2): 105-109.Mao Y, Ma J G, Bao Q L.Real-time compensation technology of time delay unit of fiber optic gyro[J].Opto-Electronic Engineering, 2009, 36(2): 105-109.

[4]Zhou Y, Zheng Z, Wu S L.Signal delay reconstruction method based on dynamic index and complex-coefficient Lagrange interpolation[J].Chinese Journal of Electronics,2015, 24(4): 750-754.

[5]Tang X J, Wei J L, Chen K.A Chebyshev-Gauss pseudospectral method of solving optimal control problems[J].Acta Automatica Sinica, 2015, 41(10): 1778-1787.

[6] 嚴恭敏, 張強, 何昆鵬, 等.捷聯慣導系統中加速度計的時延補償研究[J].宇航學報, 2013(12), 34(12): 1578-1583.Yan G M, Zhang Q, He K P, et al.Study on time-delay compensation for accelerometers in SINS[J].Journal of Astronautics, 2013, 34(12): 1578-1583.

[7]嚴恭敏, 嚴衛生, 徐德民, 等.激光陀螺捷聯慣導系統中整周期采樣的修正研究[J].傳感技術學報, 2008,21(6): 998-1001.Yan G M, Yan W S, Xu D M, et al.Correction study on dithered laser gyro whole cycle sampling demodulation in SINS[J].Chinese Journal of Sensors and Actuators, 2008,21(6): 998-1001.

[8]Wang Z, Yang Y, Lu P, et al.Optically compensated polarization reciprocity in interferometric fiber-optic gyroscopes[J].Optics Express, 2014, 22(5): 4908-4919.

[9]Ping L, Wang Z, Luo R, et al.Polarization non-reciprocity suppression of dual-polarization fiber-optic gyroscope under temperature variation[J].Optics Letters, 2015, 40(8):1826-1829.

[10]Wang Z, Yang Y, Lu P, et al.All depolarized interferometric fiber optic gyroscope based on optical compensation [J].IEEE Photonics Journal, 2014, 6(1): 7100208.

[11]Rajulapati R M, Nayak J, Sk N.Modeling and simulation of signal processing for a closed loop fiber optic gyro’s using FPGA[J].International Journal of Engineering Science and Technology, 2012, 4(3): 947- 959

[12]任剡, 房建成, 許端.直升機光纖陀螺 IMU 抗振設計及實時濾波方法[J].北京航空航天大學學報, 2013,39(4): 437-441.Ren Y, Fang J C, Xu D.Anti-vibration design and real-time filter methods for FOG IMU used in helicopter[J].Journal of Beijing University of Aeronautics and Astronautics,2012, 4(3): 947- 959

[13]Li J L, Fang J C, Du M.Error analysis and gyro-bias calibration of analytic coarse alignment for airborne POS[J].IEEE Transaction on Instrumentation and Measurement, 2012, 61 (11): 3058-3064.

Time-delay compensation method of FOG based on Lagrange interpolation

ZHANG Feng, HUANG Ji-xun, WANG Song-bang
(Beijing Aerospace Times Optical-Electronic Technology Co., Ltd, Beijing 100094, China)

The time delay link exited in fiber optic gyroscope (FOG) would affect the inertial navigation system positioning accuracy.Based on the principle of gyroscope, the time delay mechanism of FOG and the relationship between delay characteristic of different azimuth FOGs and navigation positioning precisions were analyzed.On this basis, the time delay compensation method based on Lagrange interpolation is proposed to get the alignment information at that moment by Lagrange interpolation extrapolation, so as to realize the FOG output time registration in the three directions.Simulation and multi-degree of freedom navigation experiments verify the validity of the theoretical analysis and the compensation method.With this method, the accuracy of navigation system is improved by 21%.

FOG; positioning accuracy; Lagrange interpolation; multi-degree of freedom navigation

U666.1

A

1005-6734(2017)05-0676-05

10.13695/j.cnki.12-1222/o3.2017.05.020

2017-05-23；

2017-08-28

“863-706”重大專項（2007AA704206）

張峰（1982—），男，高工，博士研究生，從事導航、制導與控制技術研究。E-mail: guyansnow@126.com