三浮陀螺磁懸浮干擾力矩機理分析

王 雪，鄧忠武，馬 寧

（1.北京航天控制儀器研究所，北京 100854；2.陜西航天時代導航設備有限公司，寶雞 721000）

三浮陀螺磁懸浮干擾力矩機理分析

王 雪1，鄧忠武1，馬 寧2

（1.北京航天控制儀器研究所，北京 100854；2.陜西航天時代導航設備有限公司，寶雞 721000）

在三浮陀螺磁懸浮的干擾力矩研究方面，詳細分析了磁懸浮干擾力矩的產生機理，對機加和裝配誤差、磁性材料的不理想、調試過程等可能造成的磁懸浮干擾力矩進行了定性分析和定量計算，推導出干擾力矩的表達式，并通過組合加工的方法對磁懸浮干擾力矩的力臂加以控制。目前的加工水平可以達到：徑向磁懸浮干擾力矩1×10-8N·m，對應的陀螺漂移8.4×10-2(°)/h，隨機分量4.2×10-6(°)/h；軸向磁懸浮干擾力矩2×10-10N·m，對應的陀螺漂移1.7×10-3(°)/h，隨機分量為 8.4×10-8(°)/h。

三浮陀螺；磁懸浮；干擾力矩；機理分析

三浮陀螺儀是在單自由度液浮積分陀螺基礎上研制的高精度慣性器件。“三浮”是指其陀螺馬達采用動壓氣體支承，陀螺輸出軸采用液浮+磁懸浮的支承方式。磁懸浮一方面可以消除剩余的重浮力差，使浮子組件處于懸浮狀態；另一方面可以使浮子精確定中，有效地提高了陀螺的精度和穩定性[1-2]。

作為慣性導航系統的核心部件，陀螺儀的精度與導彈的命中精度密切相關，通常用陀螺的漂移來對其進行表征。陀螺漂移由陀螺輸出軸上存在的各種干擾力矩引起[3-7]。為降低輸出軸軸承的干擾力矩，三浮陀螺采用磁懸浮支承確保了浮子軸尖與寶石軸承不接觸，完全消除了機械接觸摩擦引起的干擾力矩，但是，它給陀螺帶來了新的誤差源——磁懸浮干擾力矩。磁懸浮干擾力矩對儀表輸出的常值漂移和隨機漂移都會產生影響[8-11]。磁懸浮干擾力矩與磁懸浮元件的機械加工精度和工藝要求、軟磁材料的磁性能、浮子定中位置的選取等要素密切相關。

1 機加裝配的影響

磁懸浮元件（特別是磁懸浮轉子）的機加和裝配的精度是造成磁拉力產生干擾力矩的主要原因。由于機加和裝配過程中的不理想是永遠無法完全消除的，為了提高陀螺的使用精度只能對磁懸浮干擾力矩進行抑制。進行抑制的前提是要對可能造成干擾力矩的各種因素的作用機理進行理論分析和估算。

從干擾力矩的作用形式和產生機理來看，磁懸浮干擾力矩主要分為由軸向、徑向磁懸浮，它們有很大區別，下面分別進行分析和計算。

1.1 徑向磁懸浮干擾力矩的分析

按照誤差的來源，可將徑向磁懸浮的干擾力矩分為圓度誤差干擾力矩和安裝誤差干擾力矩兩部分。1）圓度誤差干擾力矩

圓度誤差干擾力矩是指由于轉子表面加工的幾何誤差所引起的干擾力矩，在所有類型的磁懸浮干擾力矩中占主要成分。如圖1所示，在每個徑向磁懸浮轉子上有四個獨立磁場，每對磁極間磁拉力的大小隨浮子的位置而變化。理想情況下，徑向磁懸浮轉子外圓如圖2中虛線所示，受轉子外圓圓度誤差的影響，實際轉子表面情況如實線所示。磁懸浮轉子所受到的磁拉力方向始終垂直于轉子表面，如果磁拉力的作用線不通過整個轉子的中心，就將產生干擾力矩。

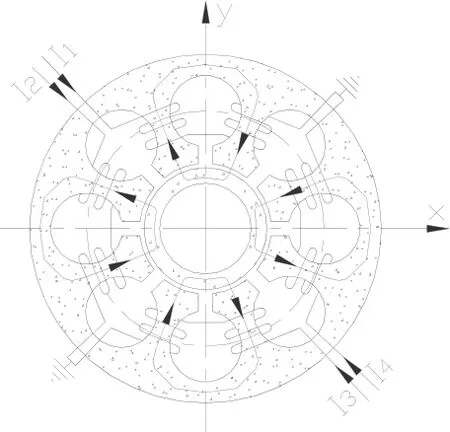
圖1 徑向磁路示意圖Fig.1 Radial magnetic circuit diagram

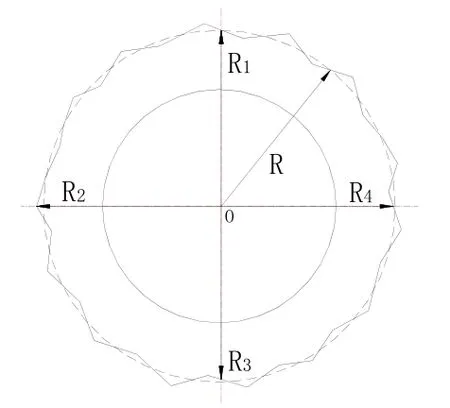
圖2 徑向轉子表面示意圖Fig.2 Radial rotor surface diagram

為分析簡便，假設轉子沿軸向方向是均勻的，這樣就可以通過建立二維平面視圖來分析轉子圓度誤差所產生的徑向干擾力矩。如圖3所示，將轉子表面劃分為和理想表面存在不同夾角的微小折線。首先計算轉子的某一小段折線AB和轉子母線構成/的微小面積上的磁拉力dF產生的干擾力矩。

設AB所對應的圓心角為dθ，由于dθ很小，故：

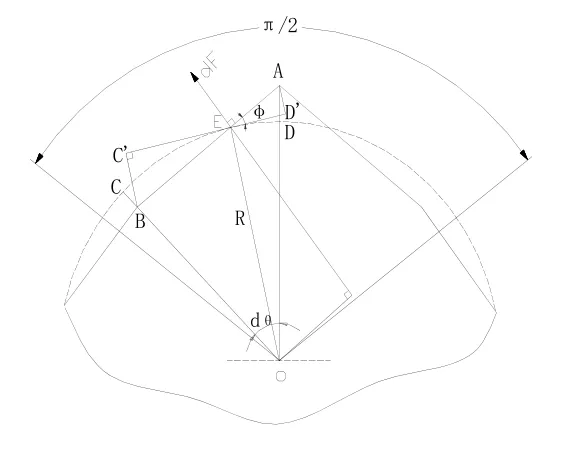
圖3 徑向轉子圓度誤差干擾力矩分析示意圖Fig.3 Disturbance moment analysis schematic diagram of radial rotor roundness

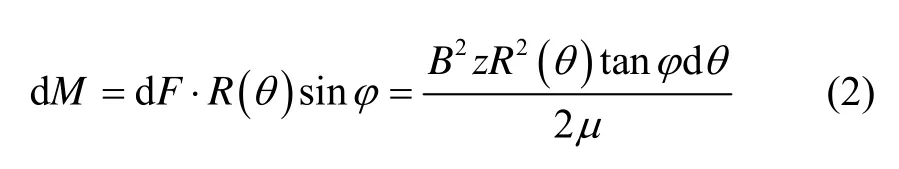
式中，

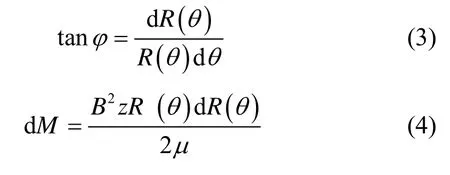
其中：z為徑向轉子長度；B為轉子表面磁感應強度，它是角度θ的函數；為沿轉子圓周方向所取微元的起點和終點所對應的半徑差。在每一個獨立磁場覆蓋下的圓弧段內，B可以認為是常數，即：

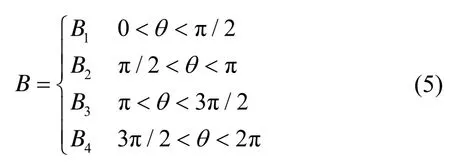
由徑向轉子的圓度誤差造成的第i對徑向磁極的干擾力矩：

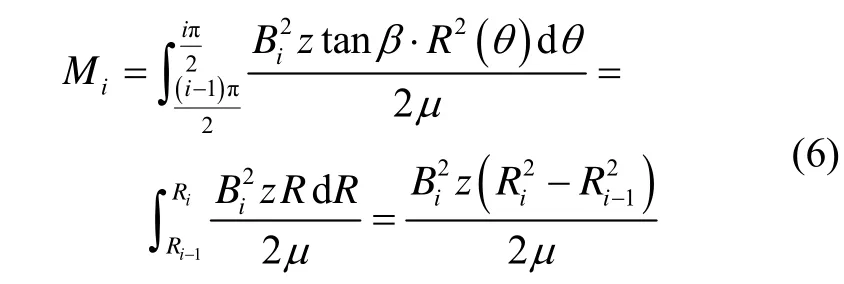
在2π范圍內求其代數和，得到圓度誤差造成的整個徑向轉子的干擾力矩：

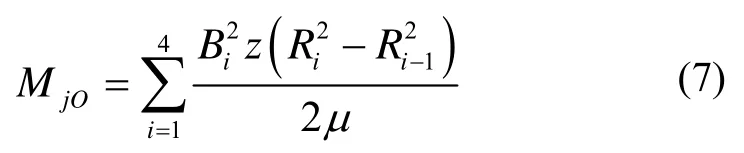
式中：Ri、Ri-1分別為第i對徑向磁極沿轉子圓周方向的起點和終點所對應的半徑差。

由式(7)可以看出，磁懸浮的圓度誤差干擾力矩和B的平方成正比。雖然在每一個獨立磁場覆蓋下的圓弧段內，B可以認為是常數，但磁懸浮在工作過程中，由于浮子位置的不確定性使得徑向磁懸浮元件之間工作氣隙的長度在很小范圍內是隨機的，而B隨定、轉子相對位置的變化而變化，因此，磁懸浮的圓度誤差干擾力矩在磁懸浮工作過程中存在一定的隨機分量，隨機分量的大小與式(7)計算的常值分量成正比，與磁懸浮工作氣隙長度變化量的平方成正比。

由式(7)得：

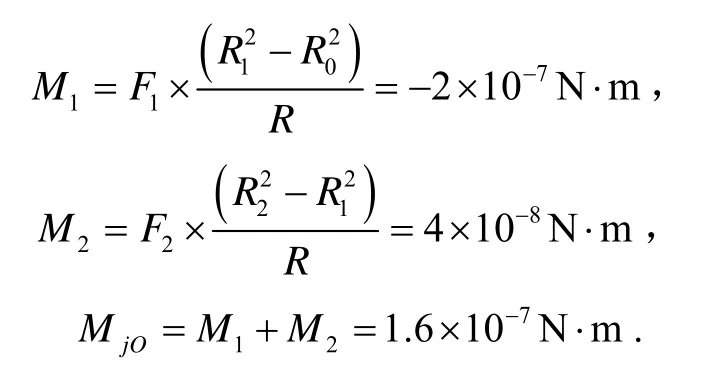
設磁懸浮工作氣隙長度為0.08 mm，變化量為5μm，參考MjO的推導過程，其隨機分量為

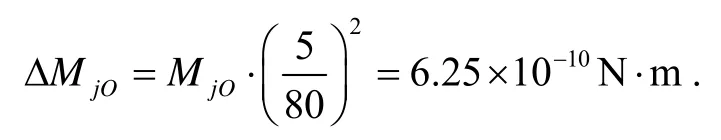
2） 安裝誤差干擾力矩

在沒有安裝誤差的理想情況下，徑向磁懸浮定子軸線與陀螺輸出軸平行，轉子軸線與陀螺輸出軸和浮子軸重合。此時，每對徑向磁極產生的磁拉力的方向都與浮子軸共面且垂直，不會產生繞浮子軸的干擾力矩。實際裝配情況如圖4所示。由于安裝誤差的影響，使得徑向定、轉子軸線與浮子軸都存在夾角，轉子軸向與浮子軸OF之間還有一定的偏心。

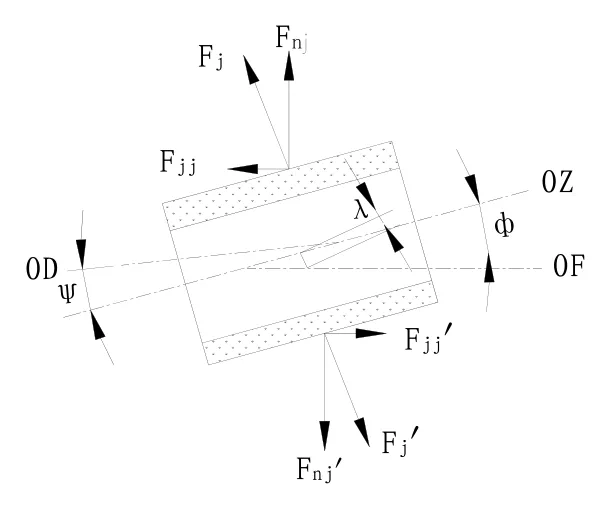
圖4 徑向轉子實際安裝示意圖Fig.4 Radial rotor actual installation diagram

圖4中，OF為浮子軸，OZ為徑向轉子軸線，OD為徑向定子軸線，ψ、Φ分別為徑向轉子軸線與浮子軸和徑向定子軸線之間的夾角，λ為徑向轉子中心與浮子軸之間的偏心距。ψ、Φ的存在改變了徑向磁懸浮定、轉子元件之間的工作間隙沿轉子軸線方向的均勻性，使得磁極間的磁拉力Fj、Fj′的方向與實際轉子的表面垂直而不垂直于浮子軸。磁拉力可以分別分解成平行于浮子軸方向的Fjj、Fjj′和垂直于浮子軸方向的力Fnj、Fnj′，這兩對力產生的力矩均垂直于浮子軸方向。因此，由安裝誤差造成的徑向轉子軸線與浮子軸的夾角和徑向轉子軸線與徑向定子軸線之間的夾角不會產生繞陀螺浮子軸方向的干擾力矩。

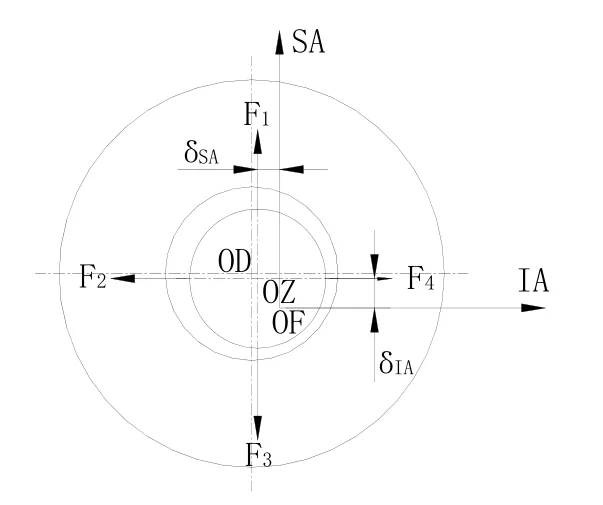
圖5 浮子受力圖Fig.5 Float free-body diagram

下面計算圖 5中徑向磁懸浮轉子相對浮子軸的偏心δ引起的繞陀螺浮子軸的干擾力矩。將δ分解成沿陀螺的自轉軸SA的分量δIA和沿輸入軸IA的分量為由圖5得到由于偏心δ所產生的繞浮子軸的干擾力矩：

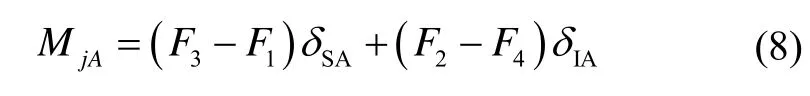
磁拉力：

則：

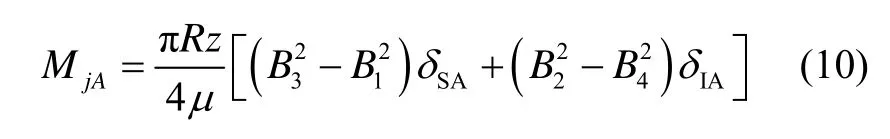
由式(10)可以看出，MjA和轉子表面磁感應強度B的平方成正比。與圓度誤差干擾力矩一樣，MjA在磁懸浮工作過程中也存在一定的隨機分量，它與式(10)計算的常值分量成正比，與磁懸浮工作氣隙長度變化量的平方成正比。

一般情況下，如不采取特殊措施，徑向磁懸浮轉子與陀螺框架的同軸度為 5～10μm，假設其沿SA、IA方向的分量徑向磁懸浮的磁拉力1F、F4均為0.05 N，F2、F3均為零，則徑向磁懸浮因偏心產生的干擾力矩為：

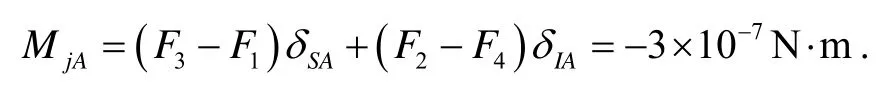
磁懸浮工作氣隙長度為0.08 mm，變化量為5μm，則隨機分量為：陀螺電機角動量為它對陀螺造成的漂移隨機分量為

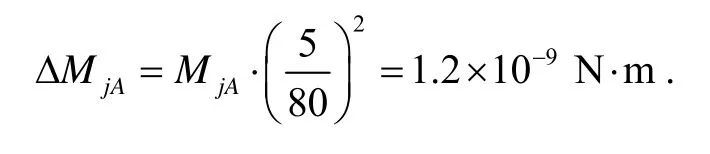
1.2 軸向磁懸浮干擾力矩的分析

理想情況下軸向磁懸浮定、轉子的對稱軸都與陀螺浮子軸重合，定、轉子的表面互相平行并與浮子軸垂直。這時，磁懸浮定、轉子之間的氣隙均勻且垂直于浮子軸。系統工作時磁懸浮定子線圈通電，定、轉子和氣隙形成電磁通路，氣隙中的磁力線互相平行且垂直于定、轉子表面，定、轉子之間的磁拉力方向與磁力線方向一致且平行于浮子軸，軸向磁拉力不會產生繞陀螺浮子軸方向的干擾力矩。機加和裝配精度的影響使得軸向磁懸浮的實際工作情況如圖6所示。

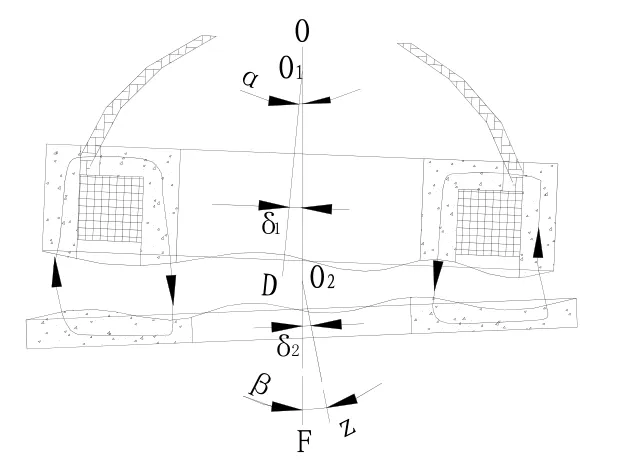
圖6 軸向元件實際安裝示意圖Fig.6 Actual installation diagram of axial elements

磁懸浮定、轉子元件的對稱軸O1D、O2Z與陀螺的浮子軸都有一定的夾角α、β和偏心δ1、δ2，定、轉子安裝平行度和轉子表面加工平面度的影響使得定轉子之間的氣隙不均勻，造成了軸向磁懸浮轉子所受到的磁拉力并不完全平行于浮子軸的方向。

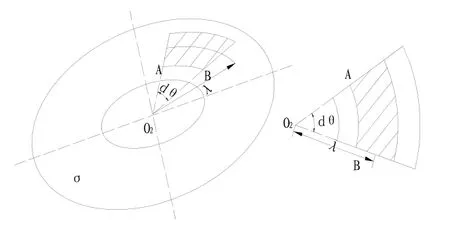
圖7 軸向轉子表面微元示意圖Fig.7 Tiny unit diagram of axial rotor surface

在圖 7中，設σ為理想平面（σ與浮子軸垂直），圖中所示圓環為實際的軸向磁懸浮轉子在理想平面上的投影。在平面σ上沿著轉子表面的圓周方向任取一段微小圓弧AB，它對應的圓弧角為dθ，并將dθ對應的轉子表面積記為dS，如圖中陰影部分所示。理想情況下，微元dS所受的磁拉力方向應垂直于平面σ。然而，由于各種不理想情況的存在使得實際轉子與理想平面不重合，因此，理想平面上的微元dS所對應的實際轉子所受到的磁拉力并不垂直于平面σ，而垂直于其實際轉子表面。假設實際轉子的受力為圖8中所示dFz的方向。

將轉子所受到的電磁拉力dFz沿理想轉子所在平面σ分解為切向力dFj和徑向力dFn。只有切向力產生繞浮子軸方向干擾力矩，若按干擾力矩最大時的條件計算時，

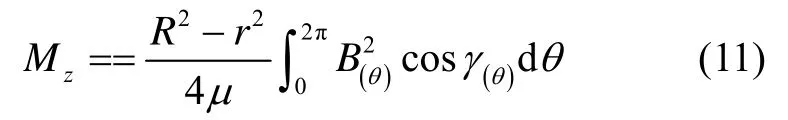
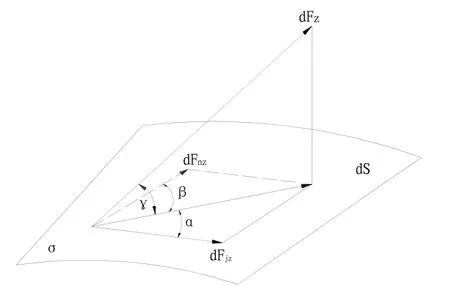
圖8 軸向轉子微元受力分析Fig.8 Stress analysis of axial rotor tiny unit

磁懸浮軸向的干擾力矩與軸向磁懸浮元件自身的平面度，磁懸浮定轉子安裝的平行度有關。當元件自身的平面度很好，磁懸浮定轉子安裝的平行度比較理想時，定轉子之間的磁場可視為均勻磁場，軸向磁懸浮的干擾力矩可以得到抑制。

軸向磁懸浮的磁拉力方向沿著輸出軸方向，當陀螺沿輸出軸方向有過載時，剩余重浮力差將由軸向磁懸浮來承載，而軸向磁懸浮干擾力矩的存在是產生三浮陀螺項漂移的因素之一。設軸向磁拉力為0.05N，軸向元件的定轉子平行度為5μm，軸向轉子平面度為1μm時，根據行位誤差的傳遞機理，軸向磁懸浮作用力的等效力臂約為軸向磁懸浮的最大徑向分力約為 0.5mg，此時，軸向磁懸浮造成的沿輸出軸方向的干擾力矩約為對應的陀螺漂移ωd≈隨機分量可見，軸向磁懸浮干擾力矩遠小于徑向磁懸浮干擾力矩。

2 磁性材料的影響

2.1 渦流損耗

按照材料劃分，三浮陀螺磁懸浮元件可分為鎳鐵疊片和鐵氧體。從作用機理上來看，磁性材料引入干擾力矩的主要途徑是磁性材料的不均勻性和各向異性引起磁通密度分布的畸變，而這類不均勻性和各向異性又引起了渦流分布和磁滯損耗的不對稱。在滿足一定條件下可以近似認為，在鎳鐵疊片元件中鐵芯損耗是渦流損耗，在鐵氧體元件中鐵芯損耗是磁滯損耗。

渦流損耗主要從磁懸浮元件的功耗方面考慮。小的渦流損耗的熱效應本身不會對儀表有嚴重的影響，因為與溫控系統產生的熱量相比鐵芯損耗的熱效應要小得多，但隨著時間和環境條件的變化，渦流分布的不對稱造成的機械不穩定可能影響到元件的幾何形狀，結合第1節的分析可知幾何形狀的不對稱會帶來干擾力矩。

渦流效應抑制的是磁懸浮元件的設計內容，從對儀表精度的影響考慮，還是要對渦流損耗加以嚴格控制的。通常可以采用兩種方法來降低材料的渦流損耗：一是采用熱軋或冷軋的方法將鐵磁材料軋成薄片疊起來使用以降低材料的厚度，二是在金屬磁性材料加入合金元素以提高材料的電阻率。

2.2 磁滯損耗

與渦流損耗類似，磁滯損耗也會提高系統的平均功耗進而降低系統的剛度。磁滯損耗對磁懸浮性能的影響可以通過品質因數表現出來。降低磁滯損耗的最好辦法是減小材料的矯頑力，矯頑力的降低會使磁滯回線變窄以減小它所圍成的面積，而面積減小的實質是能量損耗的減小。

在慣性儀表中抑制磁滯干擾力矩的主要途徑是從磁性材料的選擇出發，盡量選擇磁滯角小的材料。三浮陀螺用鎳鐵疊片鐵芯代替鐵氧體磁芯，在降低磁滯的同時減小了材料的加工難度。

3 調試過程的影響

三浮陀螺調試過程中的濕對中過程確定了浮子的定中位置，定中位置決定了磁懸浮的磁拉力的分布，磁拉力與力臂共同作用形成了力矩，因此，不同定中位置對應著不同的干擾力矩。

定中位置有兩個選擇，一個是磁懸浮定子的幾何中心，另一個是寶石軸承的中心。原則上，一般把定中位置選在寶石軸承的中心，此時軸尖與寶石軸承之間相對距離最遠，系統的可靠性和安全性最高，但這時由于磁懸浮元件的各極加力不完全通過浮子軸，就會帶來磁懸浮干擾力矩。

為了提高儀表性能，除了應根據實際情況選取合適的定中位置外，最根本的還是要對磁懸浮元件的加工和儀表的裝配過程加以嚴格的要求和控制，盡量保證磁懸浮力中心和輸出軸結構中心的重合度。

4 結 論

從磁懸浮系統自身出發，深入地討論了機加和裝配精度、磁性材料以及調試過程對磁懸浮干擾力矩和儀表精度的影響。從磁懸浮干擾力矩產生機理可以看出：磁懸浮元件的加工精度和裝配精度是產生磁懸浮干擾力矩的主要的原因，它決定了磁懸浮作用力相對于浮子軸的力臂。磁性材料和調試過程也對磁懸浮干擾力矩有所影響。

為了降低磁懸浮系統的干擾力矩，可以從以下三方面著手：設計上，選擇渦流損耗和磁滯損耗小的材料；機加上，采用組合加工的辦法提高磁懸浮元件相應部位的加工精度，其中包括提高徑向磁懸浮轉子圓度、徑向磁懸浮轉子和陀螺框架的同軸度，軸向磁懸浮轉子的平面度，軸向磁懸浮定、轉子平行度；裝配和調試上，采用精細裝調來進一步抑制磁懸浮干擾力矩。

（References）：

[1]王巍.慣性技術研究現狀及發展趨勢[J].自動化學報,2013, 39(6): 723-729.Wang W.Status and development trend of inertial technology[J].Acta Automatica Sinica, 2013, 39(6): 723-729.

[2]王立旭, 常曉華, 楊云翔.國外戰略導彈制導系統慣性器件發展趨勢分析[J].航天控制, 2016, 34(2): 95-98.Wang L X, Chang X H, Yang Y X.Development tendency analysis of the inertia device in foreign strategic missile[J].Aerospace Control, 2016, 34(2): 95-98.

[3]Su B K, Li Y B, Liu Y, et al.Improved gyroscopic drift test scheme by low-angle servo method[J].Journal of Chinese Inertial Technology, 2010, 18(6): 766-770.

[4]Wang S M, Meng N.A new multi-position calibration method for gyroscope’s drift coefficients on centrifuge[J].Aerospace Science and Technology, 2017, 68: 104-108.

[5]Shen Y, Hasanyan D, Gao J Q, et al.A magnetic signature study using magnetoelectics laminate sensors[J].Smart Material and Structures, 2013, 22: 095007(1-7).

[6]楊孟興, 吳遼, 王卿, 等.基于位置信號的三浮陀螺儀有源磁懸浮干擾力矩補償方法[J].中國慣性技術學報,2015, 23(6): 812-817.Yang M X, Wu L, Wang Q, et al.Disturbance-torque compensation for active magnetic bearing of three-floated gyroscope based on position signal[J].Journal of Chinese Inertial Technology, 2015, 23(6): 812-817.

[7]于佳福, 徐靜.三浮陀螺儀磁懸浮軸承干擾力矩測控技術[J].導航與控制, 2014, 13(1): 15-28.Yu J F, Xu J.The technology for measuring and controlling the disturbance torque for magnetic bearing of three-floated gyroscope[J].Navigation and Control, 2014,13(1): 15-28.

[8]Wang X, Zhu Z G, Deng Z W.Optimal design of magnetic suspension system in three-floated gyroscope[C]//Proc of 2010 international symposium on inertial technology and navigation.Nanjing, China, 2010: 288-293.

[9]郝晨, 張衛均, 姜大千, 趙斌.提高三浮加表磁懸浮工作精度的工藝研究[C]//中國慣性技術學會第七屆學術年會論文集.武漢, 中國, 2015: 216-221.Hao C, Zhang W J, Jiang D Q, et al.Study on technology of improving the working precision of PIGA[C]//Proc.of 2015 International Symposium on Inertial Technology and Navigation.Wuhan, China, 2015: 216-221.

[10]Hutterer M, Kalteis G, Schrodl M.Redundant unbalance compensation of an active magnetic bearing system[J].Mechanical System and signal Processing, 2017, 94: 267-278.

[11]Zheng S, Han B, Wang Y, et al.Optimization of damping compensation for a flexible rotor system with active magnetic bearing considering gyroscopic effect[J].IEEE/ASME Transactions on Mechatronics, 2015, 20(3): 1130-1137.

Mechanism analysis on magnetic suspension bearing disturbance moment in three-floated gyroscope

WANG Xue1, DENG Zhong-wu1, MA Ning2
(1.Beijing Aerospace Control Instrument Research Institute, Beijing 100854, China;2.Shaanxi Space Time Navigation Equipment Co., Ltd, Baoji 721000, China)

On the research of the disturbance moment of magnetic suspension bearings in three-floated gyroscope, the author analyzed the mechanism and carried on the qualitative analysis and quantitative calculation on the disturbance moment that might be caused by the error in the process of machining, and the un-ideal of the magnetic material, assemblage and debugging.The expression is deduced, and the force arm is restricted by the combining processing.Currently, it can be achieved that: the radial disturbance moment is 1×10-8N·m, the gyro drift is 8.4×10-2(°)/h, and the random component is 4.2×10-6(°)/h; the axial disturbance moment is 2×10-10N·m, the gyro drift is 1.7×10-3(°)/h, and the random component is 8.4×10-8(°)/h.

three-floated gyroscope; magnetic suspension; disturbance moment; mechanism analyzing

U666.1

A

1005-6734(2017)05-0681-05

10.13695/j.cnki.12-1222/o3.2017.05.021

2017-06-27；

2017-09-25

總裝預研項目（51309050101）

王雪（1981—），女，高工，從事三浮陀螺儀表研究。E-mail: woshimao9216@sina.com

聯 系 人：鄧忠武（1971—），男，研究員。E-mail: dzweng@126.com