探究SOLO分類評價理論在初中數學教學中的應用
劉凱迪


目前,我國初中數學還在積極推進新課程的改革,作為佛山市的數學中考,在2016年才跟隨廣東省的中考,縱觀2016年廣東省中考數學試卷,特別是最后的壓軸題,體現了SOLO分類評價理論,而SOLO分類評價理論是著名教育心理學家比格斯(J.B.Biggs)首創的一種學生學業評價方法,是一種以等級描述為特征的性質評價方法,這種評價方式已經在教學上得到了廣泛的應用。
一、SOLO分類評價的理論含義
“SOLO”是英文“Structure of the Observed Learning Outcome”首字母的縮寫,原意是“觀察到的學習成果的結構。根據學習者在解決學習任務時表現的不同,SOLO分類評價理論將學習成果劃分為五種復雜性水平或五種結構,其含義如下:
(1)前結構層次:學生基本上無法理解和解決問題,只提供了一些邏輯混亂或沒有論據支撐的答案。
(2)單點結構層次:學生找到了一個解決問題的思路,但卻就此收斂,單憑一點論據就跳到答案上去。
(3)多點結構層次:學生找到了多個解決問題的思路,但卻未能把這些思路有機地整合起來。
(4)關聯結構層次:學生找到了多個解決問題的思路,并且能夠這些思路結合起來思考。
(5)拓展抽象結構層次:學生能夠對問題進行抽象的概括,從理論的高度來分析問題,而且能夠深化問題,使問題本身的意義得到拓展。
從SOLO的分類方法中,看到學生的思維結構是由一個簡單到復雜的過程,也可以說是從點、線、面、立體的發展過程。
二、SOLO在分類評價在數學中考題的體現
數學中的邏輯思維是嚴謹的,條理是很清晰的,學生在解題時書寫的邏輯性和條理性更能反映學生數學思維到達的層次。例如:2016年廣東省數學中考試卷的第25題,下面分析本題SOLO分類評價在數學中考題的體現。
如圖1、圖2,BD是正方形ABCD的對角線,BC=2,邊BC在其所在的直線上平移,將通過平移得到的線段記為PQ,連接PA、QD,并過點Q作QO⊥BD,垂足為O,連接OA、OP。
(1)請直接寫出線段BC在平移過程中,四邊形APQD是什么四邊形?
(2)請判斷OA、OP之間的數量關系和位置關系,并加以證明。
(3)在平移變換過程中,設y=S△OPB,BP=x(0≤x≤2),求y與x之間的函數關系式,并求出y的最大值。
運用SOLO分類評價理論,學生回答本題的思維層次大致劃分為:
(1)前結構層次:這些學生基本上無法理解和解決問題,只是看圖形亂猜測第(1)小題答案,(2)(3)小題則無法回答。
(2)單點結構層次:這些學生沒有看到問題的本質,只看到圖形的特征就得到答案是平行四邊形,這樣的回答可能是片面的理由就得出結論,而對于后面的兩個問題卻無從下手。
(3)多點結構層次:這些學生找到了解決問題的思路,根據平移的性質,可得PQ,根據一組對邊平行且相等的四邊形是平行四邊形,從而進一步解決后面的問題。
(4)關聯結構層次:這些學生找到了多個解決問題的思路,根據正方形的性質,平移的性質,可得PQ與AB的關系,根據等腰直角三角形的判定與性質,可得∠PQO=∠OBQ,根據全等三角形的判定與性質,可得AO與OP的數量關系,根據余角的性質,可得AO與OP的位置關系。
(5)拓展抽象結構層次:這些學生能夠對問題進行抽象的概括,從二次函數的性質來分析問題,而且能夠根據等腰直角三角形的性質求出OE的長,再根據三角形的面積公式得到二次函數,這種能夠對實際問題進行抽象的數學化,把實際問題進行分類討論,從而使問題本身的意義得到拓展。
三、SOLO分類評價在數學教學的應用
從分析中考題想到,現在初中教育推行的小組合作模式以及怎樣使用三維導學案,這些教學手段更適合用SOLO分類評價的方法。
下面,探究初中數學九年級上冊的第1課時《菱形的性質》運用SOLO分類評價法在教學的應用。(這里只展示兩個環節,即“預習案”和“學習案”)
本課的核心目標:理解菱形的概念,掌握菱形的性質并能應用這些知識進行有關的計算和證明。我們運用SOLO分類設置問題,在“預習案”的【課前導學】設置為:
閱讀課本P2-P4,完成下列內容。
1. 菱形的定義:有一組____的平行四邊形叫做菱形。
2. 探索菱形的性質:由定義可知,菱形是特殊的平行四邊形,所以它具有平行四邊形的一切性質,但又有自己的獨特的性質。填寫上表:
3. 在菱形中,連接兩條對角線后,你能發現哪些特殊的三角形?各有幾個?
4. 根據菱形中出現的特殊三角形,我們在解決問題時,會用到的知識點可能有哪些?
單點結構層次是問題1,多點結構層次是問題2,關聯結構層次是問題3,拓展抽象結構層次是問題4. 學生在自主預習中去理解菱形的定義以及菱形的性質,把菱形的特征對比平行四邊形的特征,并能發現異同點,對一些思維層次高的學生進一步發現菱形的是由一些特殊的三角形構成,在解決問題時能把這些特殊的三角形性質綜合運用,這樣在預習中讓各層次的學生都能發揮自己的數學思維,到達自主學習的目標。
【嘗試練習】1. 菱形具有而一般平行四邊形不具有的性質是( )
A. 對角相等
B. 對邊相等
C. 對角線互相垂直
D. 對角線互相平分
2. 菱形的周長為20㎝,它的邊長為____。
3. 如圖3,已知在菱形ABCD中,AC與BD相交于點O,AC=24,DB=10,
(1)菱形的邊長為____,周長為____。endprint
(2)試求菱形的面積。
【嘗試練習】設置三個題目,為不同層次的學生提供不同水平的問題,那么老師在上課前了解學生的學習結果,區分學習結果的層次也就一目了然,而且更加清楚地顯示學生對某個問題的認知水平,也為師生提供有關教學質量的信息,這樣的思維層次有利于教師制定教學目標,為在課堂上解答學生的疑難問題更加準確到位,大大提高了課堂效率。
“學習案”是課堂的質量和效果的保證,本環節設置銜接“預習案”的內容,進一步把問題深化、拓展、延伸,本環節設置為:
【知識點撥】1. 由菱形是軸對稱性圖形,可以直觀理解它的性質;
2. 運用菱形的性質,結合等腰三角形性質或勾股定理解決問題。
【課內訓練】
1. 下列圖形中,不是軸對稱圖形的是()
A. 等腰三角形
B. 平行四邊形
C. 角
D. 菱形
2. 如圖4,菱形ABCD中∠DAB=60°,則∠ABD=____。
3. 邊長為4的菱形,它的一個內角等于60°,則菱形的兩條對角線的長度分別為____、____。
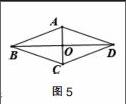
4. 如圖5,在菱形ABCD中,AC和BD是兩條對角線,
(1)若AB=6㎝,則BC=____,周長為____。
(2)若∠ABC=40°則∠BAD=____ ,∠ABD=____,∠BAC=____。
5. 如圖6,在菱形ABCD中,AC和BD相交于點O,AC=8,BD=6。
(1)求菱形的邊長;
(2)求菱形的面積;
(3)求菱形的高DE。
【課內訓練】問題1是單點結構層次,學生對軸對稱概念理解就可以回答的,問題2是多點結構層次,學生要理解菱形的定義和等腰三角形的性質才能回答,問題3、4是關聯結構層次,用到的知識有菱形的定義和性質、等腰三角形的性質、勾股定理等,問題5是前幾個結構層次的綜合。課堂是面向全體學生,分層遞進,讓全體學生都能參與課堂學習,運用SOLO分類的理論指導課堂,更加明確學生的思維水平,更利于培養學生學習的積極性和主動性。
四、SOLO分類評價的優越性
在教學中不斷滲入SOLO分類的評價法,前面只是嘗試在講授新課的探究,SOLO評價更應該在復習課中進行,這樣有助于對學生的思維層次的劃分;有助于教師教學的目標實現;有助于教師進行教學效果的檢測;有助于為高思維能力的學生提升得更高更快;有助于對學生的評價深入到了質的層面,從而達到新課程教學改革的目的,更為教學質量的提升提供多一個渠道。
責任編輯 徐國堅endprint

