論在解題教學中如何培養學生的思維品質
胡明秋
摘要:初中數學教學的核心是發展學生的思維能力。在實施素質教育的今天,如何通過解題教學培養學生的思維能力是實施創新教育、素質教育、培養新世紀新型建設人才的時代要求,也是數學教學肩負的責任。我認為在解題教學中應從培養學生思維的變通性、靈活性、嚴謹性、深刻性、獨創性著手。
關鍵詞:數學;解題教學;培養;思維品質
一、 一題多解,培養思維的變通性
一題多解的實質是以不同的論證方式,反映條件和結論的必然本質聯系,在教學中,要挖掘題目的多解因素,引導學生從多種途徑,用多種方法去思考問題,從而培養思維的變通性。
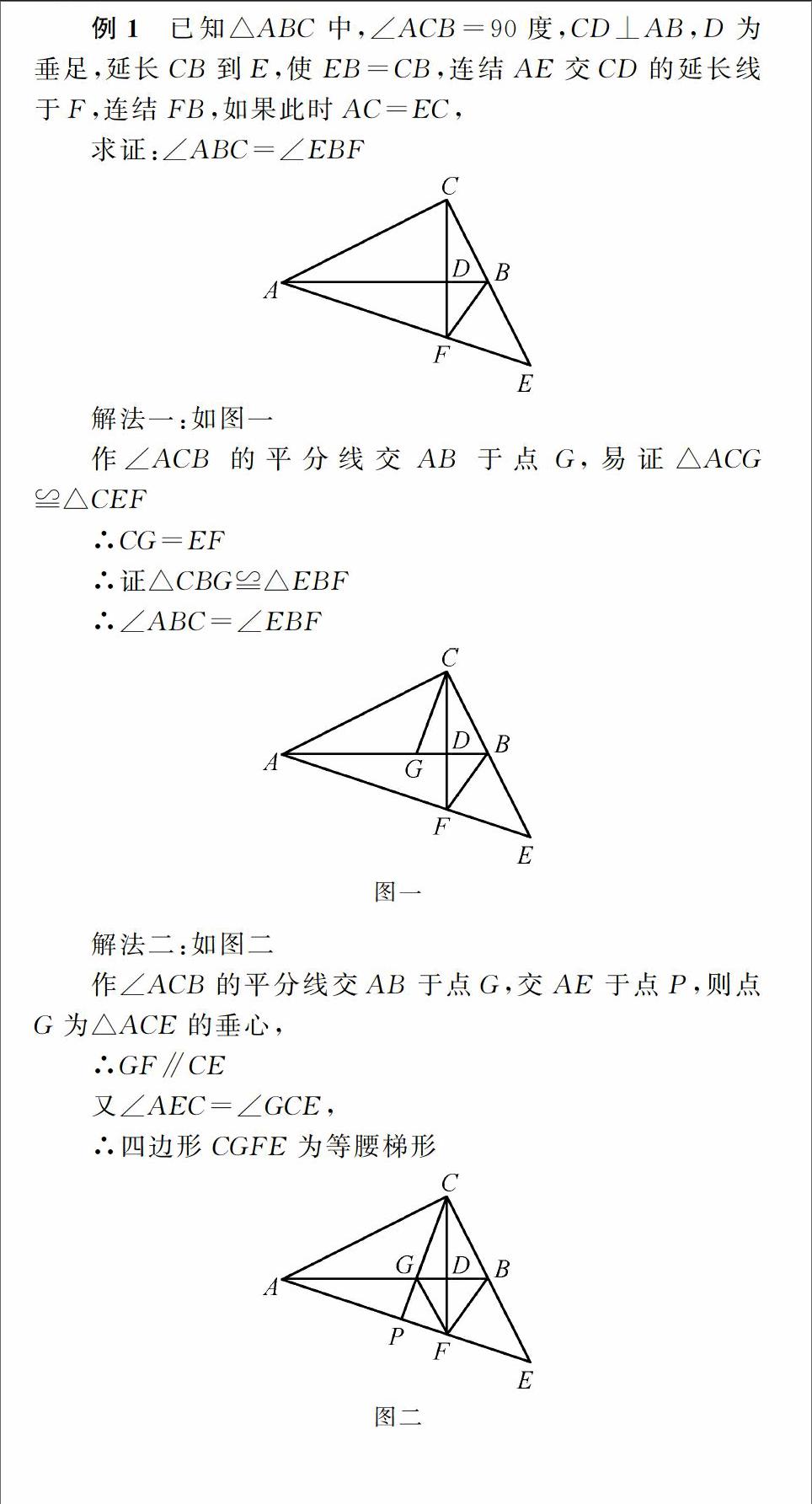
例1已知△ABC中,∠ACB=90度,CD⊥AB,D為垂足,延長CB到E,使EB=CB,連結AE交CD的延長線于F,連結FB,如果此時AC=EC,
求證:∠ABC=∠EBF
解法一:如圖一
作∠ACB的平分線交AB于點G,易證△ACG≌△CEF
∴CG=EF
∴證△CBG≌△EBF
∴∠ABC=∠EBF
圖一
解法二:如圖二
作∠ACB的平分線交AB于點G,交AE于點P,
則點G為△ACE的垂心,
∴GF∥CE
又∠AEC=∠GCE,
∴四邊形CGFE為等腰梯形
圖二
∴CG=EF
∴再證△CBG≌△EBF
∴∠ABC=∠EBF
通過一題多解,溝通了各種知識的內在聯系,使已學知識形成系統,同時學生也會從不同的角度去觀察思考問題,掌握變異規律,靈活地應用所學的知識去解決問題,這樣能夠更深刻地理解和牢固掌握所學知識,有利于提高思維的變通性。
二、 一題多變,培養思維的靈活性
一題多變是指變換題目的條件和結論,變換圖形的位置或結構,變換題目的形式以及對題目進行引申、推廣等,即將一題演變成多題,而題目的實質不變,通過解答這樣的問題,使學生能根據變化的情況思考從中找出它們之間的聯系與區別,以及特殊與一般的關系,通過尋找解決的辦法,從而使學生舉一反三,觸類旁通,培養了學生思維的靈活性。
例2已知C為AB上一點,△ACM和△CBN為等邊三角形。求證:AN=BM
(一) 條件不變,變為開放型命題
變題1:設CM,CN分別交AN,BM于點P,Q,AN,BM交于R,問題中還有其他結論嗎?并給予證明。
(2)條件不變,延伸結論
變題2:C為AB上一點,△ACM、△CBN都是正三角形,若AC=2,BC=3,則△MCQ與△BNQ的面積比為。
(三) 條件不變,變為探索性命題
變題3:在四邊形ABCD中,E為AB上一點,△ADE和△BCE是正三角形,AB,CD,DA的中點分別為P,M,N,在BC上是否存在一點Q,使四邊形PQMN是菱形?若存在,請求出Q點的位置,若不存在,說明理由。
(四) 變換條件,尋根究底
變題4:分別以△ABC的兩邊AB和AC為邊,向外作等邊△ABD和△ACE,求證:CD=BE
通過一題多變,不僅串聯了一系列知識點,滲透了數學的重要思想方法,而且提示了各方面知識的內在聯系和規律,培養了思維的靈活性。
三、 轉化解題思維,滲透數學思想方法,培養思維的嚴謹性
在教學中,常有這樣的現象,教師投入的時間和精力不少,而實際教學效果卻不令人滿意,學生做的習題不少,但還缺乏舉一反三和獨立分析問題、轉化問題和解決問題的能力。執果溯因,往往與學生的思維定勢和教師偏重知識傳授、輕視數學素質培養直接相關,因此,在解題教學中要注重解題思維,滲透數學思想方法。
例3求證:關于x的方程(x-a)(x-a-b)-1=0有兩個實數根,其中一個大于a,另一個小于a。分別設y=(x-a)(x-a-b)-1,因為此函數二次項系數為正,所以圖像開口向上,又當x=a時,函數值為y=-1<0,這說明圖像與x軸有兩個交點,且這兩交點分布在點(a,0)兩側,從而方程(x-a)(x-a-b)-1=0一定有兩個實數根,且一根大于a,另一根小于a。
四、 抓住問題的本質,培養思維的深刻性
思維的深刻性,表現在善于透過問題的現象看本質,促使學生的思維能力進一步提高。在解題教學中,教師應引導學生認真審題、分析、觀察條件特殊時的特殊情形,并注重量變到質變的關節點,剖析問題的實質,使思維更深入一步,以獲得問題解決的巧妙途徑。
例如,在復習二次根式的兩個重要公式:(a)2=a(a≥0)和a2
=|a|時學生極易混淆。因此有意放在一起,先比較兩個公式的運算順序,啟發學生找出本質上的不同:前者中的a必須是非負數,后者中的a可取任意實數,但結果一定非負,且由a本身的符號來決定結果的最后表現形式。再讓學生驗證:(2)2=2,(-2)2在實數范圍內無意義,(-2)2=|-2|=2。通過及時點撥,步步深入的分析、釋疑,減少練習中的錯誤。
五、 標新立異,培養學生思維的獨創性
思維的獨創性是以廣泛的聯想、推廣、引申及轉移、化歸等數學思想方法為基礎的,在解題教學中,要注意引導學生用常規方法去解題,但也要啟發學生獨辟蹊徑,發現新的解題思路,教會學生通過典型問題深化,推廣去發現新的方法,這對于學生發展思維的創造性無疑具有積極作用,同時也是數學素質教育的一重要方向。
例4已知4x+10y+z=169(1)
3x+7y+z=126(2)
求x+y+z的值
解:由原方程組得:
(x+y+z)+3(x+3y)=169(1)
(x+y+z)+2(x+3y)=126(2)
(2)×3—(1)×2得x+y+z=40
此題若按常規解法,需分別求出x、y、z的值,然后相加,但分析題目的內在聯系,統觀全面,解法就別開生面。
又如化簡1996×1997×1998×1999+1
分析:首先自然想到的是被開方數中“1996×1997×1998×1999”的積,其運算量大,費時費力,但抓住二次根式中的數字特點,先引入未知數化為無理式,再將被開方數化為完全平方式,從而得到化簡的結果。
解:令1996=x,則1997=x+1,1998=x+2,1999=x+3
于是:原式=x(x+1)(x+2)(x+3)+1
=(x2+3x+1)2
=x2+3x
+1=x(x+3)+1
=1996×(1996+3)+1=3990005
總而言之,在數學解題教學中,要著力培養學生思維的變通性、靈活性、嚴謹性、深刻性、創新性,使之成為21世紀的新人才。endprint

