四色猜想

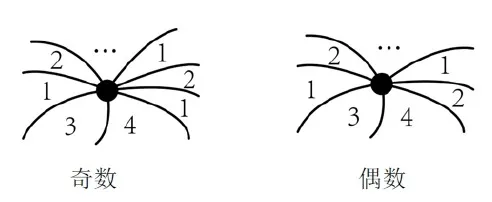
摘要：1852年，畢業于 倫敦大學的格斯里（Francis Guthrie）來到一家科研單位搞地圖著色工作時，發現每幅地圖都可以只用四種顏色著色。這個現象能不能從數學上加以嚴格證明呢？他和他正在讀大學的弟弟決心試一試，但是稿紙已經堆了一大疊，研究工作卻是沒有任何進展。1852年10月23日，他的弟弟就這個問題的證明請教了他的老師、著名數學家德·摩爾根，摩爾根也沒有能找到解決這個問題的途徑，于是寫信向自己的好友，著名數學家 哈密頓爵士請教，但直到1865年哈密頓逝世為止，問題也沒有能夠解決。1872年，英國當時最著名的數學家凱利正式向倫敦數學學會提出了這個問題，于是四色猜想成了世界數學界關注的問題。

關鍵詞：四色猜想；五色定理；

鋪瓦定理：如果任意簡單的二維圖形被分割為充分小的區域，則不論這些區域的形狀如何，必然有這樣一些點使三個或更多個區域在那里相遇，另外，一定存在圖形的這樣一種剖分，使得每個點至多同時屬于這剖分的三個區域。

我們關心的平面地圖著色問題，而不是關心一個國家疆界是正方形還是圓形，因此我們可以利用平面圖形的拓撲關系，總可以把一副簡單（幾何關系簡單不是外形簡單）圖形拓撲的等效于鋪瓦定理圖形。鋪瓦定理圖形，是一個國家最多和另外兩個國家彼此比鄰。比鋪瓦定理圖形稍微復雜一點幾何圖形關系，是一個國家被三個國家圍繞，而且其中一個國家和另外三個國家保持彼此都相鄰，這樣，顯然需要著四種顏色，要不然就要撞色。如圖：

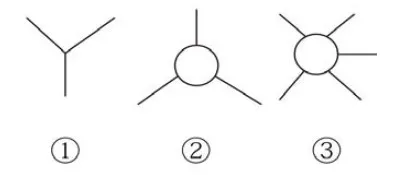
這種幾何關系，也可以把鋪瓦定理中實心點改成空心點來等效。此種幾何結構是平面幾何結構中最復雜的，如果再多一個國家就不能彼此保持這種其中一個與另外四個都彼此間相鄰的幾何關系。因此，經過上述分析，我們知道一張地圖中，不管多復雜，界點總可以分成如下三類，如圖：

可見，一副地圖著四色是平面圖形幾何結構關系決定。一副地圖著四種顏色夠嗎？這個完全取決于地圖中國家與國家疆界之間的幾何關系，而且是綜合幾何關系，而不是簡單的國家的數量。假設用1、2、3、4和5，5個數字代替5種顏色。我們知道一副地圖國與國之間存在著界線，這兩個國家和至少其他一個國家相界，那么必存在一個界點。因此，一副地圖，到處充滿著界點，而且界點是至少3個國家的界線的交點，有些是4個國家，有些是5個國家，有些甚至更多。我們規定，1個國家被超過3個，如果達8個國家圍繞，那么多出來6個國家，是偶數個，按照1-2-1-2-1-2排列；如果多出來的國家是奇數個呢？我們按照1-2-1-2-1排列，這樣排列是基于為了滿足最少著色要求。

現在我們討論第③類界點數字標注情況，我們用圖形來分析這些界點的幾何關系：

考慮最復雜的那種幾何關系；假如有兩個區域已經標注了3和4；那么，另外還有兩種情況與之共點，1、奇數個國家與之共點，根據上文最小著色要求的規定，那么只需要標注4個數字即可；2、偶數個國家與之共點，那么也只需要標注4個數字即可。具體如下圖，

根據上圖形分析，在復雜的第③類界點幾何關系下，我們標注了4個數字，如果遇到更復雜的幾何關系，我們把黑色界點標注5即可；而且，3和4如果不相鄰，那么他們之間我們可以插入標注1和2，不影響格局。地圖上出現了5，那么還會出現更復雜的幾何關系嗎？不會，我們可以用5代替3，結果仍然只需要標注4個數字，然而遇到更復雜的幾何關系（第③類界點是最復雜的幾何關系），我們用被代替3標注黑色界點即可。

另一種方法標注，我們知道地圖的界點有三類，我們從最復雜第③類界點開始標注，讓中心圓圈標注4，最復雜情況下，用1、2和3標注其他區域；接著同樣讓第②類界點中心圓圈標注4，其他顯然標注1、2和3；那么剩下地圖上都是第①類界點，而且地圖上除了圓圈內的4之外，全是1、2和3；排得好1、2和3正好排上第①類界點的三個區域；排的的不好，比如其中兩個區域已經排了1和2，剩下一個區域仍然必須排1或2，此時我們選擇4代替1或2即可；最壞的情況，就是第①類界點的三個區域必須排同樣的數字比如三個2，那么我們可以在地圖版面上交換第③類界點中的1和2的位置或者2和3的位置，或者兩者同時交換，看看還會不會出現同樣的數字同排的現象，如果仍然出現，我們用4和5代替兩個2即可，此時需著五色。

經過分析，不管地圖上國與國之間的關系多么的復雜，理論上只需著五色，即可區分國與國之間的疆界而不撞色。在實際地圖著色中，我們可以選擇第③類界點中國家數量最多那個為中心進行著色，向周圍擴散，用沒有邊界的這個條件換取第5色；更何況，我們遇不到國與國之間的復雜的幾何綜合關系，再加上選擇性著色，因此，著四色即可。

（作者：浙江省寧波市人，郵編315600）