對數學課題活動開展現狀的思考
江蘇省南京市天景山中學 章利霞
對數學課題活動開展現狀的思考
江蘇省南京市天景山中學 章利霞
數學課程標準中提出“數學教學是數學課題活動的教學”,教師應“向學生提供充分從事數學活動的機會”,讓學生在做中學、玩中學。數學課題活動有以下幾方面需要努力:意識亟待培養、方法亟待指導、素材亟待挖掘,尤其從數學課題活動的素材挖掘方面談了幾個可能的途徑,分別是:從定義中來;從定理講解中來;從例題講解中來;從實際生活中來。
數學課題活動;意識;方法;素材
一、意識亟待培養
現在的教材中,“課題學習”、“做一做”等內容所占比重較大,“做可能大的長方體”、“測量旗桿的高度”等內容,是重要的數學課題活動素材,但教學時間少,為完成教學計劃及應付考試,好多教師不重視。開展適當的活動,讓學生在不斷地嘗試——改進——再嘗試中體驗、感悟,其后再與他人交流、取長補短,增強學生的數學意識和學習態度,所以數學教師對進行數學課題活動的意識要亟待加強。
建構主義者認為:知識主要是學習者在一定的情境下,借助他人的幫助,利用必要的學習資源實現對知識的意義建構。開展好必要的活動讓學生參與進來,激發他們學習數學的興趣已刻不容緩。
二、方法亟待指導
有些教師將數學課題活動等同于數學實踐活動,熱鬧的課堂靜不下來,學生忙忙碌碌,或動手操作,或合作交流,缺少了學生獨立思考的時間和機會,而教師卻置身事外。這就對教師素質提出了更高的要求,駕馭能力、調控能力,對細節的處理要想透理清,學生可能對活動的目的暫時不太了解,而教師一定要對活動期望達到的結果心知肚明。
數學課程標準中提出“數學教學是活動的教學”,應“向學生提供充分從事數學活動的機會”,但課標所指的“教學活動”是指觀察、實驗、操作、歸納、類比、猜想、推想、論證、交流、反思等一系列的數學認知活動。
三、素材亟待挖掘
典型的數學活動主要集中在統計、頻率等少數幾個章節上,實際上,教學的很多內容稍加改造都可以成為很好的數學課題活動素材,而且在常態的課堂教學中,如果能很好地加以運用,對學生數學素養的提升可以說是潤物細無聲。
1.從定義中來,欲擒故縱,讓定義的講解不再生硬
以“三角函數”的教學為例,定義處理的一貫做法是教師先介紹sin、cos、tan的意義,并且說明是哪兩邊的比值,接著學生開始記憶、背誦并且強化訓練,學生始終處于被動地位。
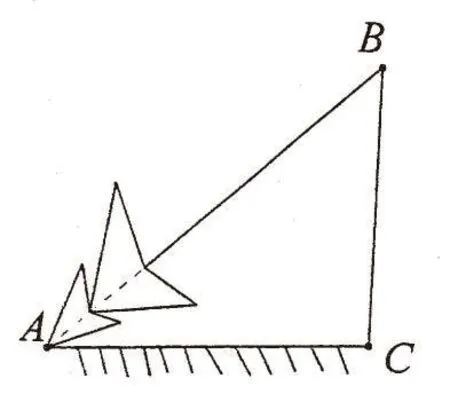
有位教師設置了這樣的情境:如圖,一棵樹在一次臺風中被攔腰折斷(∠C=90°),設在△ABC中,∠A、∠B、∠C所對的邊依次是a、b、c。依據下列數據,你能計算出這棵數的原高嗎?
(1)若∠A=30°,還需要測出哪一個數據(只允許一個),就可以計算出原樹高?為什么?怎么計算?
(2)如果測得∠A=40°,a=2米,你能求出b、c嗎?
教師通過由特殊到一般的類比,激起學生對三角形中的邊角關系的重新審視與思考,得出“當直角三角形中一個銳角一定時,那么它的三條邊之間存在某種確定的比”的關系,從而使三角函數的定義的引入順理成章。
2.從定理講解中來,讓定理的證明更加親切,在不知不覺中得以完成
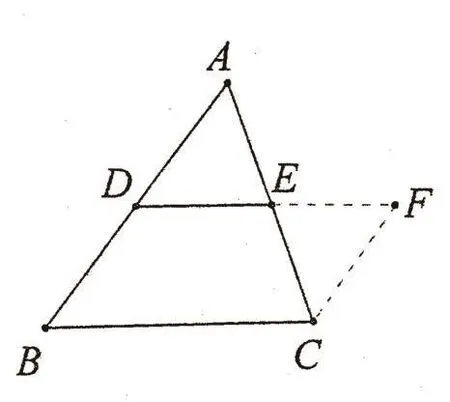
比如三角形的中位線定理的證明一直是教學中的一個難點,學生很難想到要將中位線延長構成一個平行四邊形,有的老師則很好地解決了這個問題。
師:給你一張三角形紙片ABC,你們能將它剪一刀后拼成一個平行四邊形嗎?(很快,多數學生都完成了任務)
師:你們是沿著哪一條線將三角形剪開的?這條線段的兩個端點有什么特點?
由此自然引入中位線的定義,在此基礎上,教師又適時引導學生繼續觀察圖形,問你還能得到哪些結論?
經過一番熱烈的討論,學生在互相啟發下比較順利地得到了“三角形的中位線平行于第三邊,并且等于第三邊的一半”的結論,此時教師要求學生證明這個命題,學生添加輔助線也就水到渠成了。
3.從例題講解中來,讓例題的呈現由平鋪直敘到跌宕起伏
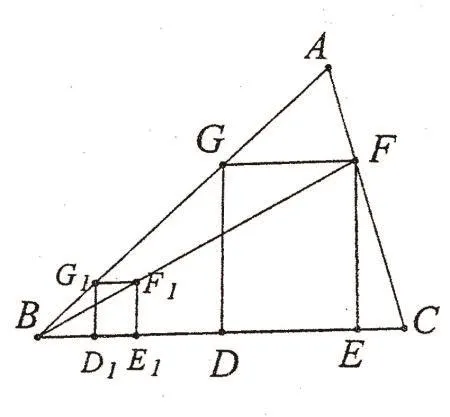
有這樣一道閱讀理解題:在給定的銳角三角形ABC中,求作一個正方形DEFG,使D、E落在BC上, F、G分別落在AC、AB邊上,作法如下:
第一步:畫一個正方形D1E1F1G1,使D1、E1落在BC上,GI落在AB邊上;
第二步:連接BFl并延長,交AC于點F;
第三步:過F點作FE⊥BC,垂足為點E;
第四步:過F點作FG⊥BC,交AB于點G;
第五步:過G點作GD⊥BC,垂足為點D。
四邊形DEFG即為所求作的正方形。你能解釋其中的原因嗎?
筆者選取了兩個不同班級進行實驗,結果大相徑庭。
在甲班按照常規的:出示例題——學生讀題——思考——教師提問——講解的常規順序進行,最大的感覺就是學生沒有多少激情,整個過程顯得非常沉悶。
而在乙班采取了下面的方法:
師:現有一張三角形紙片,你能在其中剪出一個正方形嗎?如果要剪出一個最大的正方形呢?
一石激起千層浪,學生開始積極行動,有的學生結合自己所掌握的位似的相關知識得出了正確的結論,有的學生百思不得其解,但也興趣高漲、積極嘗試,在此時把題目展示出來,很多學生“如饑似渴”地將題目讀完,效果不言而喻。
4.從實際生活中來,用數學的眼光審視身邊發生的一切
課堂時間有限,學生的課外生活也是豐富多彩的,作為數學教師,也可以要求學生通過書寫數學日記、小論文的方式引導他們關注身邊的事。
數學課題活動開展的現狀雖然還不盡如人意,但其拓展和提升的空間還很大,只要我們樹立起開展數學課題活動的意識,憤而啟、悱而發,學生的學習熱情需要我們精心設計適當的活動去激發。

