再看“三角恒等變換”

☉湖北省華中師大一附中 劉馨怡

☉湖北省華中師大一附中 周龍虎

正值高三第一輪復習之際，我們在老師帶領下有條不紊地復習“三角恒等變換”這一章節，相對于高一新課的學習多了些許感受，愿與大家分享，不當之處還請多指正.

我們的復習更重視教材的核心內容的解讀與背后思想的顯化.老師說，教材是高考命題之本，更是數學思維訓練的練兵場.在《普通高中課程標準實驗教科書·必修4》（下稱《必修4》）的第三章“三角恒等變換”的章首語中講到.

變換是數學的重要工具.在初中，我們已經學習過代數的變換，在《必修4》的第一章也學習過同名三角函數式的變換，在此基礎上，本章將學習包含兩個角的三角函數式的變換……三角變換包括變換的對象，變換的目標，以及變換的依據和方法等要素.兩角和與差的正弦、余弦與正切公式就是三角變換的基本依據.通過對這些公式的探求，以及利用這些公式進行三角變換，我們將在怎樣預測變換目標，怎樣選擇變換公式，怎樣設計變換途徑等方面作出思考，這些都將幫助我們進一步提高推理能力和運算能力.

我又查閱了百度百科關于此概念的解讀：

數學上的一類公式，用于三角函數等價代換，可以用于方便我們化簡式子，也方便運算.基本上可以從三角函數的函數圖像中推理出誘導公式，也能從誘導公式中延展出其他的公式，其中包括倍角公式、和差化積、萬能公式等.

通過對比，教材解釋得更通透些，三角恒等變換是變形而不變質的不同于代數變換的一種變換，它的角（單角或復角的關系）與名（正弦、余弦或正切等）是我們思考的起點，變換過程中的目標意識、簡化意識及公式再現意識都是無可或缺的，這樣我們才能將三角關系中的“變換”打通關.

例1 （《必修4》第141頁例4）如圖1，已知OP Q是半徑為1，圓心角為的扇形，C是扇形弧上的動點，ABCD是扇形的內接矩形.記∠COP=α，求當角α取何值時，矩形ABCD的面積最大？并求出這個最大面積.

例2 （《必修4》第146頁復習參考題A組第七題）已知cos（α+的值.

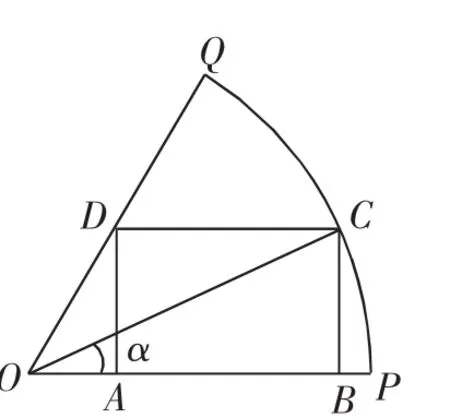
圖1

倘若直接將這兩個問題選為該章節的例題或者習題，絕對吊不起我們的胃口.不是太過簡單的緣由，而是例題不能突出課題的核心思想——變換，其承載的變換的要素太少，需要拓展.因而，通過與老師討論，得到了以下問題：

為節約篇幅，解答過程都略去.

問題1中由于沒有給出內接的形式，便存在多種可能性，增大了討論的難度，需要對邊角關系有一定的估算能力，從而得到另一種情形是矩形的一邊與OQ平行，通過作∠POQ的平分線可化歸到教材所給的模型中去；由于沒有給出“∠COP=α”這一條件，就有可能建立面積關于角（S=f（α））或者邊的函數關系（S=f（x））.巧妙的是，最終面積關于邊的函數關系中求面積的最大值，為簡化代數運算，三角代換發揮了作用，并將該函數對應關系化歸到面積關于角的函數關系上.因此，通過對問題1的變式與拓展，我們不僅體會到了三角關系的變換（輔助角公式的運用），還有三角關系與純代數關系的變換（主要是區別），不同問題的變換（主要是化歸）.

問題2討論的主要是“三角函數+方程組”形式的問題，變換的對象增至角、名及方程組，因而對方程組的常規變換方式如作四則運算、平方運算等要有一定的了解.對于第2問，從班上同學反饋的情況來看，絕大多數同學都只做到將兩個方程平方求和求出cos（x+y）的值就止步不前了，是不敢對方程組再作變換（嫌麻煩）還是欠缺變換的意識了呢（認為方程組的信息已盡數使用了）？如果是前者，對兩個方程作乘積或先平方再作差都會得到三個角（2x，2y，x-y）的三角關系式，由于忽略角“x+y”是已知角，因而不能將角“2x與2y”成功轉換為“（x+y）+（x-y）與（x+y）-（x-y）”；如果是后者，那說明對方程組的等價變形不甚了解.一般來說，方程組同解.因而缺少了必要的變換就失去了等價性，思路自然受阻.該問的探討還有一個功能，就是從角度變換上詮釋了和差化積、積化和差公式，角度的變換不是刻意為之的，是順勢而為.

數學解題是一個自覺、有趣且富有創造性的思維活動.在解題的每個階段，我們都要調整探尋方式與階段目標的關系，以確定問題的最終解決，這便是目標意識.為了確保目標能夠較快并以較簡捷的方式達成，我們還需要對思維過程進行監控.

當目標明確時，就要努力溝通已知與未知，采用綜合分析法打開局面.

題中角α雖不是特殊角，但是已知角，待求式一定可以轉化到與tanα有關的式子上，這是最終的目標.接著便是如何轉換的問題，仍舊從角與名出發.發現角再利用弦切轉換就能利用已知條件了！

當目標不太明確時，要多關注三角式的結構，往往可利用公式的結構特征進行轉換，以自然派生出最終目標.

若站位于三角恒等變換的視角，等式兩邊同時乘以sinA定是可取的（分式轉換為整式），得到sinB=sinA·cos（A+B）.根據左右兩式的結構（準確點說，是對照學習過的三角關系式，不能直接展開cos（A+B）），只得利用三角形內角和定理化兩元為三元得sinB=-sinA·cosC.一般來說，減元以逐步減少問題中變元的個數達到簡化問題的目的，然而增元亦可看成“先做退步”后的減元.相信讀者都會再現兩角和與差的正弦公式，再次利用三角形內角和定理消去角B！

若站位于解三角形的視角，無非是走“邊路線”或是“角路線”.將已知式化成=-cosC，由正余弦定理轉化為邊之間關系是及其自然的，最終再折回到目標角B上去.比起前一種做法，變換的路徑稍短些，方式自然些，效果自然不同.

值得注意的是，三角恒等變換中往往涉及三角函數的求值、求角問題，由于三角函數并非是一一對應函數關系，中間過程若涉及求角就有可能出現增根情況.

我們班上出現兩種解法：

因而，變換雖是數學的一大利器，我們仍要避免變換中的非等價性以及變換路徑過長甚至變換多向性等問題，真正在復習中提升自我的邏輯思維能力.