數(shù)形結(jié)合方法在高中數(shù)學(xué)教學(xué)中的應(yīng)用
☉江蘇省錫東高級中學(xué) 蔡曉紅
數(shù)形結(jié)合方法是數(shù)學(xué)思想方法之一,它將“數(shù)”與“形”有機地聯(lián)系到一起,實現(xiàn)了以數(shù)助形,以形助數(shù).從某種角度來講,數(shù)是形的抽象概括,形是數(shù)的直觀表現(xiàn),而對于數(shù)學(xué)知識來講,無論“數(shù)”還是“形”都是呈現(xiàn)的方式,領(lǐng)會運用“數(shù)”、“形”能夠降低數(shù)學(xué)的難度,提高學(xué)生的學(xué)習(xí)效率和質(zhì)量.因此,筆者結(jié)合多年的教學(xué)實踐經(jīng)驗,概述了數(shù)形結(jié)合方法在高中數(shù)學(xué)教學(xué)中的應(yīng)用原則,并從定義、性質(zhì)及同角這三個方面,探究了數(shù)形結(jié)合方法在三角函數(shù)中的應(yīng)用,以期數(shù)學(xué)結(jié)合方法能夠科學(xué)、合理地運用到數(shù)學(xué)中,使學(xué)生掌握靈活運用數(shù)形結(jié)合方法的技巧,提高學(xué)生的解題效率和正確率.
一、數(shù)形結(jié)合方法在高中數(shù)學(xué)教學(xué)中的應(yīng)用原則
數(shù)形結(jié)合思想既是一種解題思想,又是一種解題方法.在數(shù)學(xué)教學(xué)中,數(shù)形結(jié)合思想是指,通過數(shù)量關(guān)系轉(zhuǎn)化為空間圖像、空間圖像轉(zhuǎn)化為數(shù)量關(guān)系,實現(xiàn)“數(shù)”、“形”兩者結(jié)合的解題思想和方法.通過研讀高中教科書發(fā)現(xiàn),教材中擁有大量、復(fù)雜的空間圖像問題和數(shù)量關(guān)系問題,而在解決問題的過程中,教師如若能夠潛移默化地將“數(shù)形結(jié)合方法”滲透其中,既能夠降低學(xué)生“學(xué)”和教師“教”的難度,還能夠提高學(xué)生“學(xué)”和教師“教”的效率.可見,數(shù)形結(jié)合方法運用到高中數(shù)學(xué)教學(xué)中具有必要性.而數(shù)形結(jié)合方法應(yīng)用于高中數(shù)學(xué)教學(xué)中,不要盲目實施,而是要尊重等價性和雙向性原則,否則會適得其反.
等價性原則主要是指在“數(shù)”與“形”轉(zhuǎn)化的過程中,要確保“數(shù)”與“形”的對等.實踐證明,數(shù)形結(jié)合方法確實能夠降低某些問題的難度,激發(fā)學(xué)生解題的積極性,提高學(xué)生解題的效率和正確率,但是如若“數(shù)”與“形”轉(zhuǎn)化不等價,就定然不會獲取正確的答案.
雙向性原則就是指在分析數(shù)量關(guān)系和空間圖像的過程中,實現(xiàn)“數(shù)”與“形”的優(yōu)勢結(jié)合.如在求取函數(shù)最值問題時,就要將函數(shù)圖像與“數(shù)”進(jìn)行整合,這樣以來,通過觀察圖像,就能夠輕易獲取正確的答案,若數(shù)形結(jié)合方法未遵循“雙向性原則”,解題過程可能會出現(xiàn)各種問題,進(jìn)而與正確答案失之交臂,而“數(shù)”與“形”的轉(zhuǎn)化也失去了應(yīng)有的意義.
二、數(shù)形結(jié)合方法在三角函數(shù)教學(xué)中的應(yīng)用實踐
數(shù)形結(jié)合方法是數(shù)學(xué)教學(xué)中常用的解題思路和方法,實踐證明,科學(xué)合理地運用數(shù)形結(jié)合方法,不僅能夠提高課堂的教學(xué)質(zhì)量和效率,還能夠強化學(xué)生對于數(shù)學(xué)知識的理解,促使學(xué)生完成知識內(nèi)化.而三角函數(shù)作為高中數(shù)學(xué)的重要組成部分,它具有抽象性、難度大等特點,導(dǎo)致學(xué)生學(xué)習(xí)的興趣不高,導(dǎo)致課堂的教學(xué)效果不甚理想.結(jié)合三角函數(shù)相關(guān)知識的特征,筆者在日常的教學(xué)中,采用了數(shù)形結(jié)合方法,取得了理想的教學(xué)效果.
1.數(shù)形結(jié)合方法在三角函數(shù)定義教學(xué)中的應(yīng)用
從定義來看,三角函數(shù)就是數(shù)形結(jié)合的產(chǎn)物,因此在定義教學(xué)中,教師應(yīng)該合理地運用“數(shù)形結(jié)合方法”,強化學(xué)生對于三角函數(shù)定義的理解,從而提高學(xué)生運用“定義”解決問題的能力.結(jié)合學(xué)生解決問題的過程可以發(fā)現(xiàn),定義求解一般運用“取點法”和“單位圓”的方法,而相比較而言,單位圓的方法更為簡便,且解題的速度更快.
分析:由已知條件可知,解決此問題可以通過“取點法”、“單位圓”兩種方法進(jìn)行解題.
表1 的正弦值、余弦值、正切值的解決方法及過程

表1 的正弦值、余弦值、正切值的解決方法及過程
方法一取點法 方法二單位圓y y A圖O 60° x x M O 30°P(1,y)P(x,y)解(略) (略)將角5π 將角5π 3放置到直角坐標(biāo)系xOy中,并換一個單位圓,而角5π 3的正弦值、余弦值及正切值.3的正弦值、余弦值及正切值.備注 兩種方法都運用了數(shù)形結(jié)合法,但比較而言,單位圓較為簡潔,僅僅需要知道點P的橫坐標(biāo)就可以得到答案評注3放置到直角坐標(biāo)系xOy中,并在角的邊上取點P,并從點P向Ox的正方向引垂線PA,構(gòu)建直角△PAO.通過點P的坐標(biāo)可以得出Rt△PAO的各個邊長,然后結(jié)合定義,就可以得出角5π 3的終邊與單位圓的交點為P,并由點P向x軸引垂線PM.結(jié)合三角函數(shù)在單位圓里的特殊性質(zhì),輕松、便捷地就可以得到角5π
2.數(shù)形結(jié)合方法在三角函數(shù)性質(zhì)教學(xué)中的應(yīng)用
大多數(shù)學(xué)生對于三角函數(shù)的性質(zhì)都較為了解,但是在具體的問題中,并不能夠靈活地運用,進(jìn)而導(dǎo)致問題的解決過程不夠順利,甚至得不到正確的答案.性質(zhì)是解決三角函數(shù)相關(guān)問題的重要著手點之一,但是要想合理地運用,就需要能夠靈活地運用“數(shù)形結(jié)合方法”.因此,作為一線的教育工作者,在日常的教學(xué)實踐中,要將數(shù)形結(jié)合方法滲透到三角函數(shù)性質(zhì)教學(xué)中,使學(xué)生準(zhǔn)確把握“數(shù)”和“形”兩者之間的關(guān)系,能夠降低問題的難度,提高學(xué)生解題的正確率和效率.三角函數(shù)性質(zhì)往往被運用到不等式、不等式方程及比較大小等問題中,如若能夠?qū)⒕唧w問題轉(zhuǎn)化成為圖形,再結(jié)合性質(zhì),就能夠輕松地解決問題.
分析:單從已知條件根本找不到著手點,若了解三角函數(shù)的性質(zhì),可以將其構(gòu)建出“形”,認(rèn)真觀察,就可以得出答案.首先,根據(jù)已知條件,構(gòu)建關(guān)于未知數(shù)x的函數(shù)f(x)=sinx;然后,在直角坐標(biāo)系xOy中畫出函數(shù)f(x)=sinx的圖像(圖1);最后,結(jié)合題意和三角函數(shù)的性質(zhì),得出滿足(k∈Z).
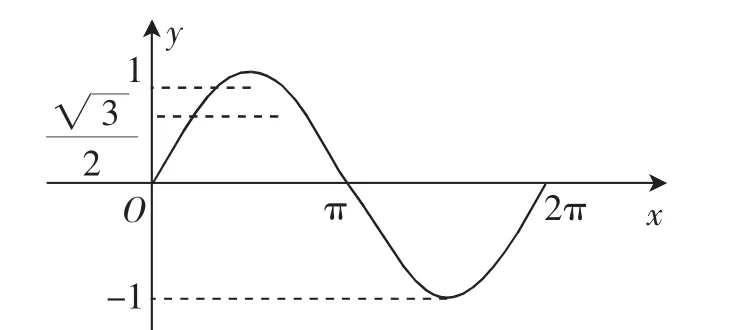
圖1 函數(shù)f(x)=sinx的圖像
評注:將問題轉(zhuǎn)化為求“角”的問題,也要運用到“數(shù)形結(jié)合方法”,它利用了正弦圖像和代數(shù)式結(jié)合的方法.針對該題目,不僅要掌握三角函數(shù)的性質(zhì),還要能夠完成構(gòu)建函數(shù)的環(huán)節(jié),并將函數(shù)圖像呈現(xiàn)于大腦中,甚至于紙張上.這樣,降低了題目的難度,還有助于拓展學(xué)生的思維.在此需要注意的就是,該題目解決的方法并僅有這一種,還有“單位圓”的方法,此文中就不詳細(xì)闡述.
3.數(shù)形結(jié)合方法在同角三角函數(shù)關(guān)系教學(xué)中的應(yīng)用
同角三角函數(shù)的關(guān)系是三角函數(shù)教學(xué)的重要內(nèi)容之一,而通過研讀數(shù)學(xué)教材發(fā)現(xiàn),同角三角函數(shù)關(guān)系可以從“數(shù)”和“形”兩個角度進(jìn)行理解和掌握.同角三角函數(shù)關(guān)系有平方關(guān)系(表2)和商數(shù)關(guān)系(表2),無論是平方關(guān)系還是商數(shù)關(guān)系都可以從“數(shù)”和“形”兩個角度進(jìn)行推導(dǎo).在實踐的應(yīng)用中,大多數(shù)學(xué)生不能夠靈活地運用三角函數(shù)的平方關(guān)系和商數(shù)關(guān)系,歸根究底就是因為學(xué)生未曾真正掌握同角三角函數(shù)的關(guān)系,導(dǎo)致在實際問題中,不能夠完成遷移,進(jìn)而導(dǎo)致出現(xiàn)各種問題,長此以往,會降低學(xué)生學(xué)習(xí)數(shù)學(xué)的興趣和欲望.
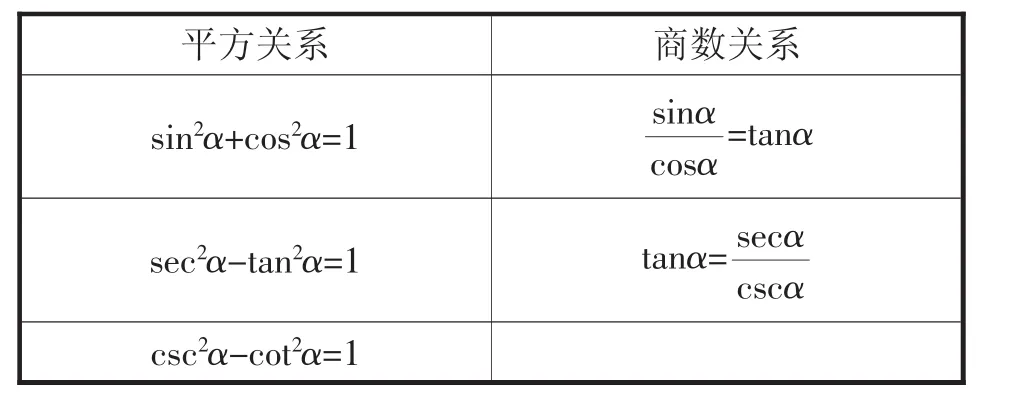
表2 同角(α)三角函數(shù)關(guān)系
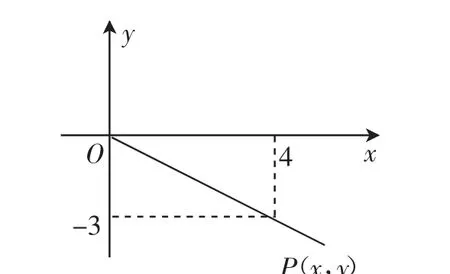
圖2 tanα=-的圖像
解:由定義和圖得知,點P的坐標(biāo)為(4,-3),|OP|=5,所以
評注:利用已知條件畫出對應(yīng)圖像,然后結(jié)合定義,就能夠直觀地將結(jié)果呈現(xiàn)于腦海中,這樣不僅避免了繁雜的代數(shù)運算,還提高了學(xué)生的解題效率,更能夠避免由于細(xì)心答疑,而出現(xiàn)“漏符號”的情況.
三、結(jié)束語
高中階段,數(shù)學(xué)學(xué)科中涉及大量的空間圖像、數(shù)量關(guān)系及數(shù)形結(jié)合的問題,而這些問題的難度并不大,關(guān)鍵就是學(xué)生能夠正確地運用“數(shù)形結(jié)合方法”.但是,由于受到各種因素的影響,部分學(xué)生對于“數(shù)形結(jié)合方法”的運用并不能夠滿足當(dāng)前解題的需求,所以作為一線的教育工作者,要認(rèn)識到數(shù)形結(jié)合方法的重要性,并將其滲透到數(shù)學(xué)教學(xué)過程中,使學(xué)生“數(shù)”、“形”轉(zhuǎn)化以及“數(shù)”、“形”結(jié)合的能力得到鍛煉和培養(yǎng),從而能夠從容面對相關(guān)問題,促使學(xué)生的解題效率和正確率得到提高.除此之外,還應(yīng)該讓學(xué)生認(rèn)識到,數(shù)形結(jié)合方法并不是萬能的,不能夠盲目運用,否則會適得其反.F

