對充要條件教學的再認知

☉江蘇省無錫市堰橋高級中學 陸旌霞

中學數(shù)學第一章集合論可以說是現(xiàn)代數(shù)學的基礎，有了集合論規(guī)范的表述，才有了后來各種數(shù)學知識的學習.集合論教學中，子集、交集、并集、全集、補集是集合中最基本的五大要點，形成了集合論的基礎.比如：子集關(guān)系是運用到各種知識銜接的重要知識.以命題為例：“若p，則q”指的是就是集合論中的子集關(guān)系，但是學生在學習中卻鮮有將知識串聯(lián)在一起思考.因此教師教學需要打通這些知識的單一性，形成教學的全方位處理，形成知識的綜合理解成為關(guān)鍵.

一、概念的認識

充要條件的概念在教材中僅僅是描述性的介紹，并沒有實質(zhì)性的闡述和解釋，常常在論壇中聽到學生這樣抱怨：充分條件是什么意思？老師叫我們記住“左邊推出右邊”叫充分條件，這是為什么？筆者認為：這樣的抱怨說明了幾個問題：第一，概念教學沒有做到真正理解，更多是以灌輸性的教學進行；第二，教師自身沒有全面思考充分條件的概念，更多地是站在孤立的角度去思考概念，發(fā)現(xiàn)概念不好闡述，因此用比較生硬的強行記憶的方式進行了灌輸.那么我們?nèi)绾卫斫獬浞謼l件的概念才是合理的？筆者認為需要結(jié)合以往的知識一起來思考、理解.

1.知識的對比

眾所周知，集合論中其實早就存在了充分條件，只是表述不一，我們挖掘其中的知識來對比概念，使其對于何為充分性有足夠的認識.觀察下表：

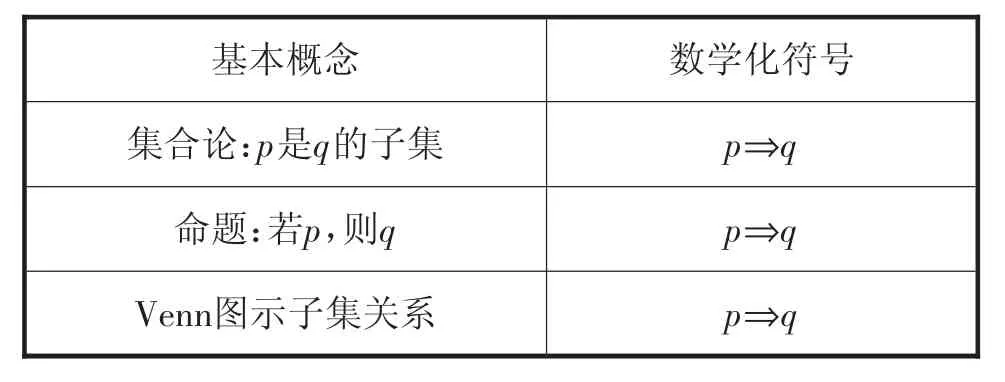
基本概念 數(shù)學化符號集合論：p是q的子集 p?q命題：若p，則q p?q Venn圖示子集關(guān)系 p?q

上述知識都是p?q的數(shù)學化符號不同形態(tài)，有子集形態(tài)、命題形態(tài)等等.這里教師需要對上述三方面知識進行合理的總結(jié)，使學生理解知識，打通這些知識之間的相關(guān)聯(lián)系.

師：我們發(fā)現(xiàn)，這些知識其本質(zhì)是一樣的，也就是說q怎么樣才能成立？

生：只要p成立，一定可以有q成立.

師：那這樣成立的條件夠充分嗎？

生：足夠充分了！

師：所以，今天我們在上述三個基本概念的基礎上，引入全新的一種更加數(shù)學化的說法：我們把p?q稱之為p是q的充分條件，意思就是條件p足夠充分推導出結(jié)論q了！

生：明白了！原來充分條件的概念非常容易理解，只要對比命題和集合論就可以了.

師：另一方面，q是p應該怎么稱呼呢？

生：集合論中沒有倒過來的講法啊！

師：的確如此.我們可以這樣想，命題q成立的時候必須要求命題p作為要求保障，因此可以說q是p的必要條件.

生：這樣對概念的理解，我們比較清楚了.

意圖：單一的概念教學顯然是比較孤立的，學生之所以不理解充分和必要，主要因素在于教師講解概念的時候過于孤立和抽象，其實引用集合論中子集的概念以及命題中“若p，則q”的表述，我們不難真正理解充分性的含義了.

2.知識的具象化

另一方面，為了進一步加深充分條件的認知，我們可以借助數(shù)學相關(guān)實驗去嘗試，這里經(jīng)典的實驗正是借助物理電器元件的電路圖來實現(xiàn)的.我們知道，電路的通暢與否很好地展示了充分與必要的關(guān)系.設“開關(guān)A閉合”為條件A，“燈泡B亮”為結(jié)論B.

分析1：觀察圖1，我們發(fā)現(xiàn)當開關(guān)A閉合時，燈泡B必然會亮，這說明“若p，則q”是成立的，即開關(guān)A閉合充分保障了燈泡B必然會亮，這是充分性最好的實驗體現(xiàn).反之，若燈泡B會亮，不能說明一定是開關(guān)A閉合的結(jié)果，有可能是開關(guān)C閉合，因此“若q則p”是不成立的，這樣來說A是B成立的充分不必要條件，因此電路實驗較好地反映了這一數(shù)學本質(zhì).

圖1

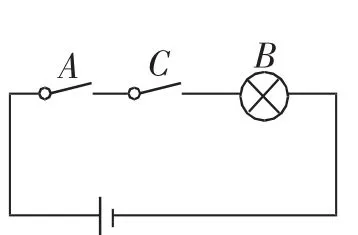
圖2

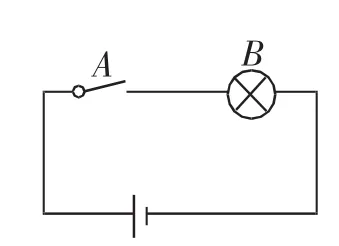
圖3

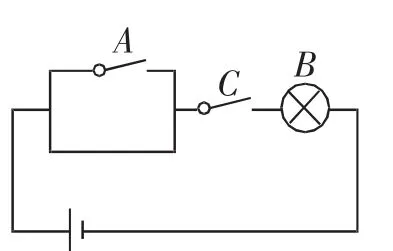
圖4

分析2：觀察圖2，我們發(fā)現(xiàn)當開關(guān)A閉合時，燈泡B不會亮，這說明“若p則q”是不成立的，即開關(guān)A閉合無法充分保障燈泡B會亮.反之，若燈泡B會亮，說明開關(guān)A必須是閉合的結(jié)果，因此“若q則p”是一定成立的，這樣來說A是B成立的必要不充分條件，因此概念的反饋躍然紙上.

分析3：觀察圖3，我們發(fā)現(xiàn)當開關(guān)A閉合時，燈泡B必然會亮，這說明“若p則q”是成立的，即開關(guān)A閉合充分保障了燈泡B必然會亮，這是充分性最好的實驗體現(xiàn).反之，若燈泡B會亮，說明一定是開關(guān)A閉合的結(jié)果，因此“若q，則p”是成立的，這樣來說A是B成立的充分必要條件，因此充要條件的數(shù)學本質(zhì)體現(xiàn)了充分的等價性原則.

分析4：觀察圖4，顯然是既不充分也不必要條件了.

意圖：數(shù)學實驗電路是充分顯示充分必要條件的一種具象化操作，這種操作大大加快了學生對于充分必要條件的理解，有了這種實驗作為保障，形成了充要條件概念的再認知，從感官角度思考得到了充分性和必要性，從而擺脫了教學的刻板和灌輸性，獲得了知識形成的過程性，符合課程標準提出的數(shù)學抽象這一最重要的核心素養(yǎng)要求.

二、問題的探索

從充要條件的概念理解來說，學生達到了一定的認知，進一步在數(shù)學學習的過程中體會充要條件是必不可少的.可以這么說，數(shù)學知識的學習可以分為三個步驟：第一是概念的學習，即通過數(shù)學具象感受數(shù)學本質(zhì)；第二是數(shù)學問題的解決，通過問題的解決豐富概念的理解，從多角度、多層次中去體會數(shù)學本質(zhì)；第三是知識的內(nèi)化，對問題進行反思，才能真正進一步的去理解知識、體會知識，這也是學習的最后層次.從本知識來說，我們通過具體案例來思考這充要條件的深刻意義.

問題1：方程x2-2mx+m-1=0有兩個不同正根，求實數(shù)的取值范圍.

分析：本題對于高一學生而言并不困難，因為大部分學生都是尊崇初中數(shù)學二次方程韋達定理這一知識尋求解決，解方程組

變式1：方程x2-2mx+m-1=0有兩個不同且大于1的根，求實數(shù)m的取值范圍.

分析：按照問題1的解決思路，學生自然形成了這樣的解題方式殊不知這樣的解決方式已經(jīng)出現(xiàn)了錯誤，這里的原因是什么呢？我們可以借助充要條件來說明這個典型的錯誤.從等價性的角度分析因此問題1的解決思路沒有任何問題，既沒有擴大解集也沒有縮小解的范圍，而之是不能成立的，即不等價，這里的反例很明顯若取無法推出這恰恰是充要條件未能保障到位的結(jié)果.這樣的問題在中學數(shù)學中往往較多的存在.

問題2：已知f（x）=ax2+cx，且1≤f（1）≤3，-1≤f（-1）≤1，求f（2）的取值范圍.

分析：這又是充分必要條件轉(zhuǎn)化不到位的一個典型問題.首先來看一看常見的錯解.

（1）+（2），得0≤2x≤4，即0≤4x≤8，（2）×（-1），得-1≤y-x≤1.（3）（1）+（3），得0≤2y≤4，故而代入f（2）=4x+2y，得0≤f（2）≤12.

顯然上述解答是有問題的，原因何在呢？其僅僅保障了問題的充分性，未能考慮到必要性，通俗的說也就是無形中放大了變量的范圍，導致求解范圍的擴大，正解范圍還應該縮小一些.看一下正解.

正解：f（2）=4x+2y=3f（1）+f（-1），由已知可得3≤3f（1）≤9，-1≤f（-1）≤1，故而兩式相加可得2≤f（2）≤10.

意圖：通過兩個經(jīng)典問題的反思，我們不難發(fā)現(xiàn)數(shù)學問題的求解探索過程就是不斷轉(zhuǎn)化充要條件的過程，將形式復雜的問題轉(zhuǎn)化為簡捷的表述，正是數(shù)學轉(zhuǎn)化與化歸思想的體現(xiàn)，這一步一步的體現(xiàn)需要一個重要的依據(jù)，即等價，也就是充要條件.

總之，數(shù)學學習的過程恰恰是充要條件的一個縮影.理解充要條件的概念反映了數(shù)學概念學習過程中具象化策略的重要性，幫助學生進一步理解充要條件對于學習數(shù)學的等價性原理、轉(zhuǎn)化化歸思想也有著極為重要的作用.對于充要條件的再認知，筆者以教學一線的實踐做了一番自我的思考，懇請讀者給予指點和斧正.

1.宋一衛(wèi).從生“動”到生動，詮釋充要條件教學［J］.中學數(shù)學月刊，2015，5.

2.方可石.邏輯教學中詮釋思維品質(zhì)［J］.數(shù)學通訊，2012，1.

3.沈恒.淺談中學數(shù)學課堂教學的適度形式化［J］.中小學數(shù)學，2010，5.