高考三視圖問題常考題型及處理策略

☉華中師范大學第一附屬中學 程季康

三視圖問題是立體幾何的入門內容，也是高考數學中的一個重要考點.翻閱近年來的高考試卷，三視圖問題是高考的必考內容；在學習之余，結合近年的高考真題，我總結近年來高考對三視圖的考查主要有以下幾個方面，現分類例析，供參考：

一、判斷幾何體的三視圖問題

給出一個幾何體的直觀圖，然后根據幾何體的形狀判斷其三視圖的問題.由于其難度較小，因此這類直接判斷型問題高考基本沒有涉及過.但在2013年和2014年的高考中，曾以空間直角坐標系中點的坐標來表示幾何體，利用考生的想象能力來判斷幾何體的三視圖的問題.

例1（2014年湖北卷）在如圖1所示的空間直角坐標系O-xyz中，一個四面體的頂點坐標分別是（0，0，2），（2，2，0），（1，2，1），（2，2，2），給出編號為①②③④的四個圖，則該四面體的正視圖和俯視圖分別為（ ）.

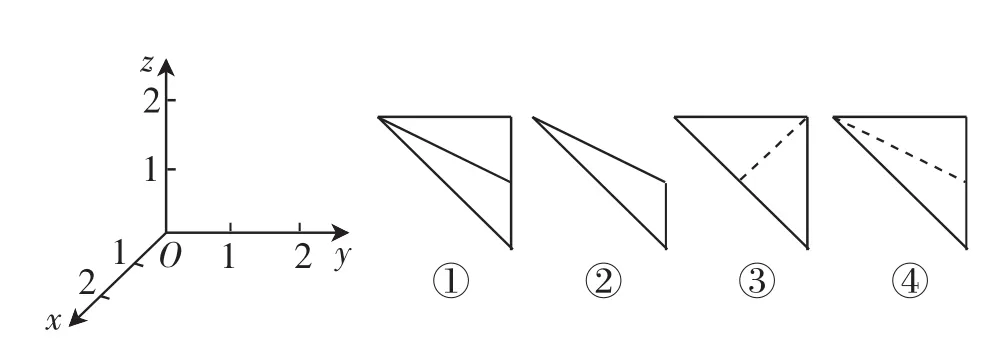
圖1

（A）①和② （B）③和①

（C）④和③ （D）④和②

解析：如圖2，將四面體放入正方體中，四面體ABCD即坐標系中四個點所圍成的四面體，顯然可以看出其正視圖為④，俯視圖為②，故選D.

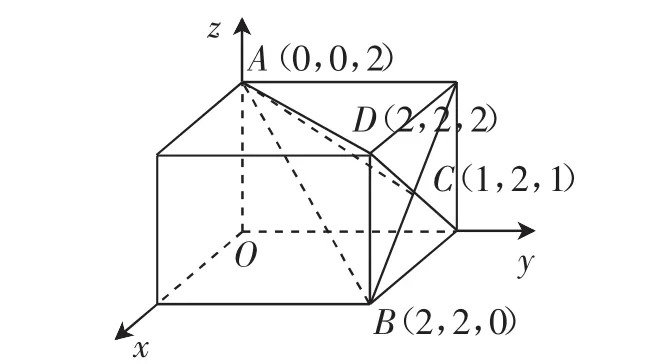
圖2

例2（2013年全國卷Ⅱ）一個四面體的頂點在空間直 角 坐 標 系 中 的 坐 標 分 別 是 （1，0，1），（1，1，0），（0，1，1），（0，0，0），畫該四面體三視圖中的正視圖時，以平面為投影面，則得到正視圖可以為（ ）.

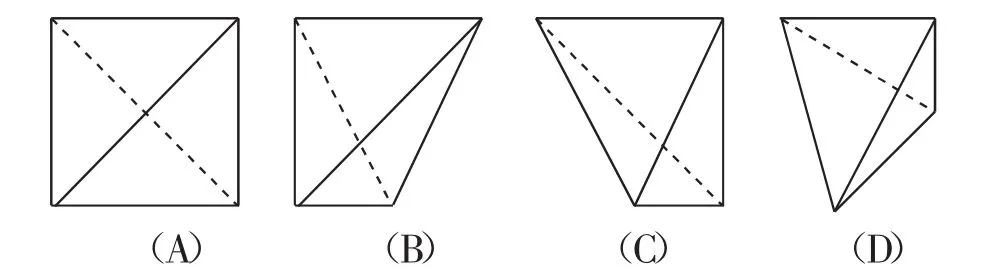
解析：在空間直角坐標系中，根據點的坐標先畫出四面體O-ABC的直觀圖，再以zOx平面為投影面，沿y軸負半軸方向看去則得到正視圖，如圖3可以觀察得到A符合要求，故選A.

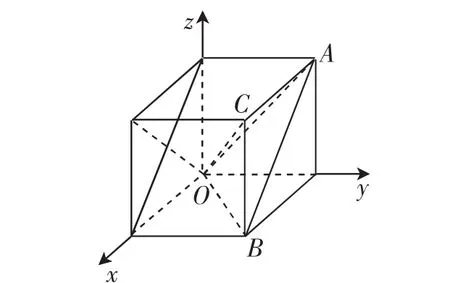
圖3

點評：上述兩題給出的均是空間直角坐標系中點的坐標，直接由點的坐標想象出空間幾何體的形狀，然后再判斷其三視圖，理論上是可以，但實際操作難度較大；此時將該幾何體在空間直角坐標系中還原，則判斷其三視圖的問題即可迎刃而解.

二、利用幾何體的三視圖還原幾何體并計算

縱觀近年來的高考試題，大多數試題是先給出幾何體的三視圖，要求計算幾何體的體積、表面積及其他量.其中以計算幾何體的體積的問題居多，其次是計算幾何體的表面積，有時也會要求計算棱長或其余與幾何體有關的量.

1.利用幾何體的三視圖計算幾何體的體積

例3（2017年北京卷）某三棱錐的三視圖如圖4所示，則該三棱錐的體積為（ ）.

（A）60 （B）30 （C）20 （D）10

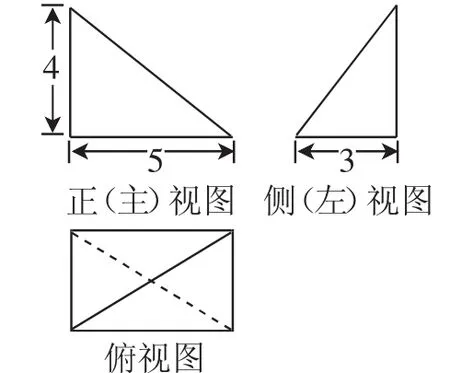
圖4

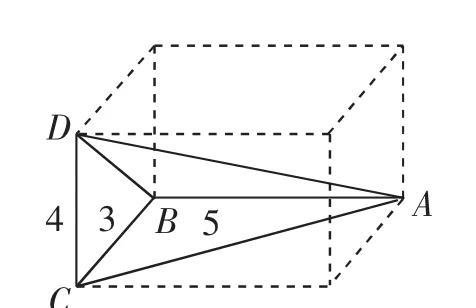
圖5

解析：根據幾何體的三視圖，還原其直觀圖，如圖5，可以看出該幾何體底面三角形兩條直角邊長為3和5，高為4，其體積為

點評：對于空間幾何體的三視圖問題，一般首先要觀察幾何體的三視圖，找出其特征及數量關系，再還原該幾何體的直觀圖；在還原幾何體的直觀圖時，對于規則的幾何圖形，一般將其放到長方體中來觀察特征，進行還原，最后根據還原后的圖形計算幾何體中邊角關系.需要注意的是本題中俯視圖中的圖形不是幾何體的底面，它只是俯視時看到的圖形而已.

例4（2017年全國卷Ⅱ）如圖6，網格紙上小正方形的邊長為1，粗實線畫出的是某幾何體的三視圖，該幾何體由一平面將一圓柱截去一部分所得，則該幾何體的體積為（ ）.

（A）90π （B）63π

（C）42π （D）36π

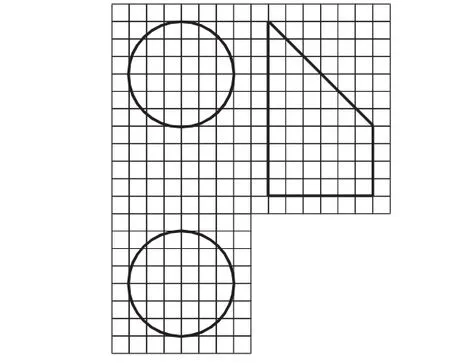
圖6

解析：由網格紙上的小正方形邊長為1可以看出該幾何體的正視圖由一個邊長為6的正方形和一個直徑為6的半圓組成，其側視圖由一個長為6，寬為4的長方形和一個直角邊長為6的等腰直角三角形組成，其俯視圖是一個直徑為6的圓；因此該幾何體的下半部分是一個底面半徑為3，高為4的圓柱；上面部分是一個底面半徑為3，高為6的圓柱切去一半所得的部分.所以其體積為.故選B.

例5（2015年課標全國卷Ⅱ）一個正方體被一個平面截去一部分后，剩余部分的三視圖如圖7所示，則截去部分體積與剩余部分體積的比值為（ ）.

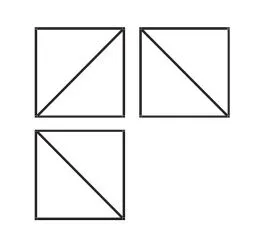
圖7

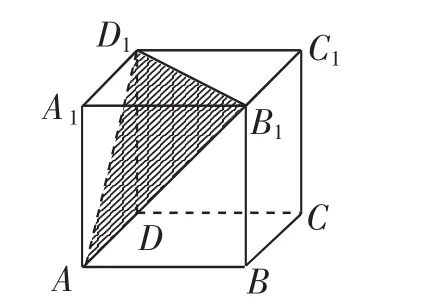
圖8

解析：根據題意，該幾何體是由一個正方體截去部分后剩下的圖形，由該幾何體的三視圖還原其直觀圖得到正方體ABCD-A1B1C1D1截去了一個三棱錐A-A1B1D1后的圖形如圖8所示.易知

點評：在由三視圖還原為空間幾何體的實際形狀時，要從三個視圖綜合考慮，根據三視圖的規則，空間幾何體的可見輪廓線在三視圖中為實線，不可見輪廓線在三視圖中為虛線.在還原空間幾何體實際形狀時，一般以正視圖和俯視圖為主，結合側視圖進行綜合考慮.求解以三視圖為載體的空間幾何體的體積的關鍵是由三視圖確定直觀圖的形狀以及直觀圖中線面的位置關系和數量關系，利用相應體積公式求解.

2.利用幾何體的三視圖計算幾何體的表面積

例6（2017年全國卷Ⅰ）某多面體的三視圖如圖9所示，其中正視圖和左視圖都由正方形和等腰直角三角形組成，正方形的邊長為2，俯視圖為等腰直角三角形.該多面體的各個面中有若干個是梯形，這些梯形的面積之和為（ ）.

（A）10 （B）12 （C）14 （D）16

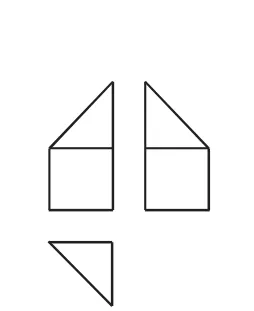
圖9

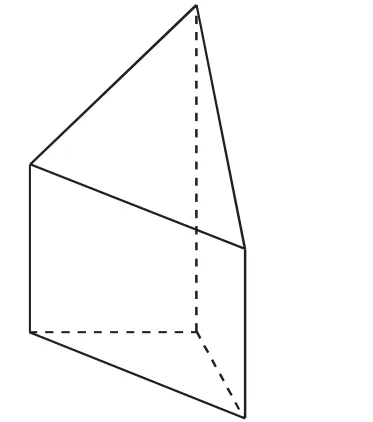
圖10

解析：根據該幾何體的三視圖可以看出該幾何體是一個三棱錐疊放在一個三棱柱上面形成的，其直觀圖如圖10所示，從直觀圖可以看出該幾何體有2個全等的梯形，其上底為2，下底為4，高為2，所以其面積之和為S=2×12.故選B.

點評：對于根據幾何體的三視圖計算幾何體的表面積問題，一般先要根據幾何體的三視圖還原其直觀圖，再根據直觀圖觀察該幾何體各個面的形狀，從而計算其表面積.

自2007年以來，埃塞通過國際竹藤組織的竹子項目引進了約20多個竹種試種，大多數竹種表現良好，其中龍竹(Dendrocalamus giganteus)、馬來甜龍竹(D.asper)、版納甜龍竹(D.hamiltonii)、黃竹(D.membranaceus)和龍頭竹(Bambusa vulgaris)建議大規模種植。

例7（2016年全國卷Ⅲ）如圖11，網格紙上小正方形的邊長為1，粗實線畫出的是某多面體的三視圖，則該多面體的表面積為（ ）.

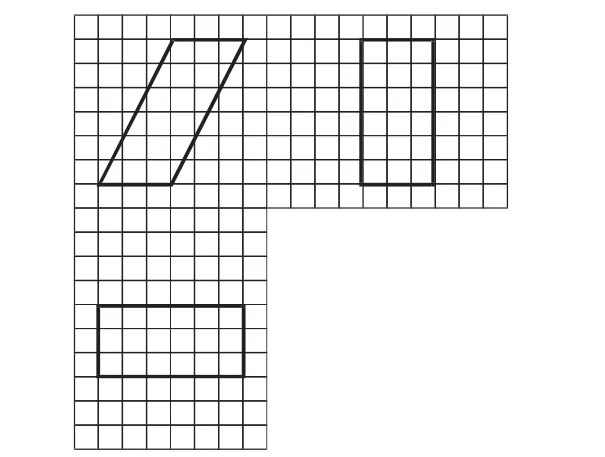
圖11

解析：根據三視圖，可以看出該幾何體是一個斜四棱柱，其底面是一個邊長為3的正方形，高為6；其正視圖看到的平行四邊形即為該幾何體的前面，顯然其是一個平行四邊形，底為3，高為6，面積為S1=3×6=18；其上下兩個面是兩個邊長為3的正方形，每一個面的面積為S2=3×3=9；其左右兩個面是兩個豎著放的長方形，底為3，高為正視圖中平行四邊形的一個邊長度為，即每一個側面的面積為.綜上，該幾何體的表面積為S=2（S1+S2+S3）=54+18.故選B.

點評：本題將三視圖放在網格中，其目的就是給出計算所需要的邊的長度.本題中幾何體的前后兩個面和上下兩個面很直觀，與其正視圖及俯視圖類似，但左右兩個側面是兩個豎放的長方形，其高線的長需要引起注意，防止出錯.

3.利用幾何體的三視圖計算幾何體中棱長或球體的半徑

例8（2017年北京卷）某四棱錐的三視圖如圖12所示，則該四棱錐的最長棱的長度為（ ）.

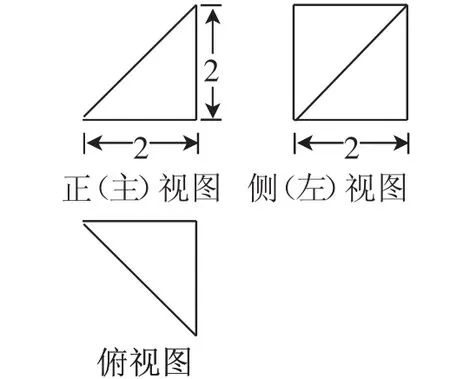
圖12

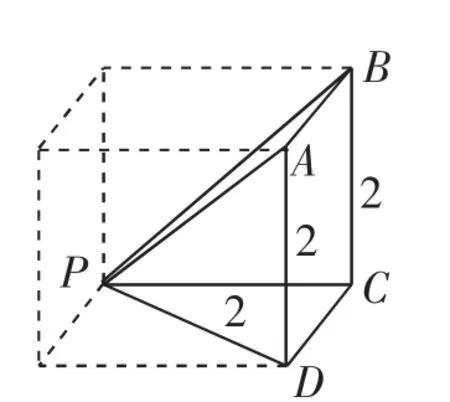
圖13

解析：根據該幾何體的三視圖，還原該幾何體如圖13所示，可以看出該幾何體是邊長為2的正方體中所截得到部分，其底面是邊長為2的正方形，頂點垂直于底面.顯然其最長棱為圖中棱PA，其長度為|PA|=.故選B.

點評：本題考查空間幾何體三視圖的識別及幾何體邊角的計算，首先要根據其三視圖還原其直觀圖，再從其直觀圖中判斷出其中最長的邊，最后根據給出的數值進行計算.

例9（2015年全國卷Ⅰ）圓柱被一個平面截去一部分后與半球（半徑為r）組成一個幾何體，該幾何體三視圖中的正視圖和俯視圖如圖14所示.若該幾何體的表面積為16+20π，則r=（ ）.

（A）1 （B）2 （C）4 （D）8

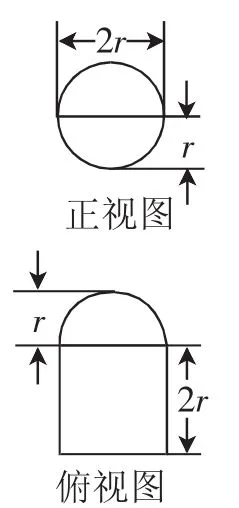
圖14

解析：由三視圖可知，此組合體的前半部分是一個底面半徑為r，高為2r的半圓柱（水平放置），后半部分是一個半徑為r的半球，其中半圓柱的一個底面與半球的半個圓面重合，所以此幾何體的表面積為2πr2=4r2+5πr2=16+20π，解得r=2.故選B.

點評：本題只給出了三視圖中的兩部分，解決的關鍵仍然是從正視圖及俯視圖中確定幾何體的形狀.從正視圖是個圓可以確定該圓柱是橫放，從俯視圖中的長方形和半圓型可以確定半球在圓柱的后面，從而利用圓柱和球體的表面積公式計算出球的半徑.

4.利用幾何體的三視圖既計算體積又計算表面積

例10（2016年全國卷Ⅰ）如圖15，某幾何體的三視圖是三個半徑相等的圓及每個圓中兩條互相垂直的半徑.若該幾何體的體積是，則它的表面積是（ ）.

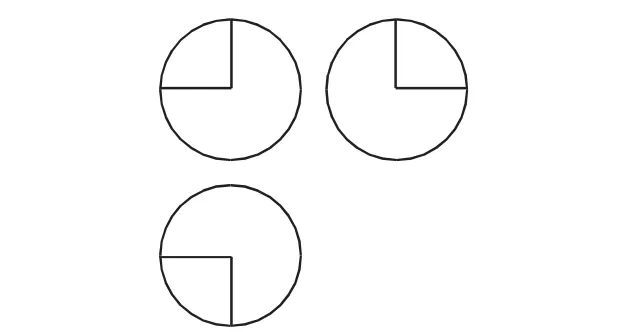
圖15

（A）17π （B）18π （C）20π （D）28π

點評：本題解題的突破口在由三視圖觀察出幾何體的形狀，從而根據體積的值計算出球體半徑的長度，最終計算出球體的表面積.

例11（2016年浙江卷）某幾何體的三視圖如圖16所示（單位：cm），則該幾何體的表面積是______cm2，體積是_____cm3.

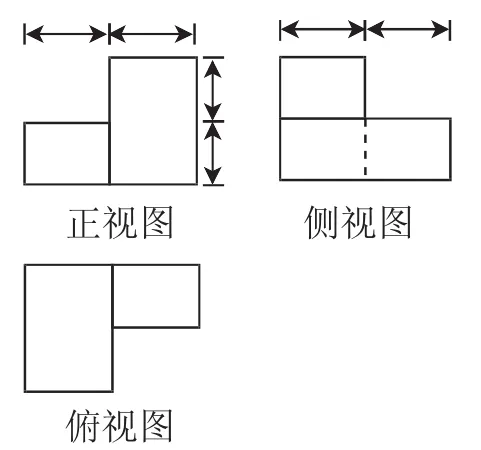
圖16

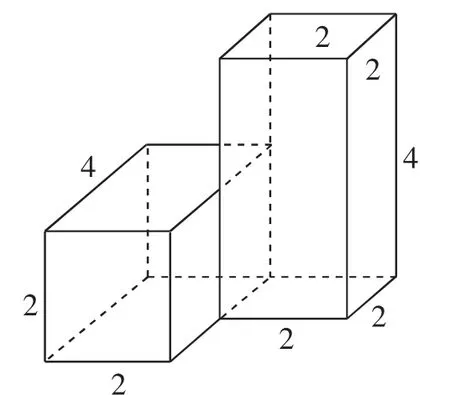
圖17

解析：根據三視圖，可以發現該幾何體是兩個相同的長方體靠在一起而形成的，它們的底面是邊長為2的正方形，高是4，其中一個“站立”，另一個“平躺”.其直觀圖如圖17所示.所以其表面積為S=2×（2×2×2+2×4×4）-2×2×2=72（cm2），體積為V=2×2×2×4=32（cm3）.

點評：本題考查三視圖的識別與幾何體的表面積與體積的計算.先根據三視圖還原幾何體的直觀圖，再計算其表面積與體積.

從上面近年來的高考真題可以看出，三視圖問題往往與幾何體的體積、表面積以及空間線面關系、角、距離等問題相結合，解決此類問題的關鍵是由幾何體的三視圖準確確定幾何體的形狀及其結構特征，然后再根據要求進行計算.一般說來，其難點主要有兩點：一是根據三視圖確定幾何體的形狀及相關數量關系；二是根據相關數量關系準確進行計算.只要解決了這兩個難點，三視圖問題一般都能迎刃而解.