以抽象思維發(fā)展為基點 提升數(shù)學(xué)課堂的有效性

李 建

（江西省豐城市石灘中心小學(xué)，江西豐城 331105）

引 言

在數(shù)學(xué)教學(xué)實踐中，教師往往忽略了學(xué)生抽象思維能力培養(yǎng)，導(dǎo)致學(xué)生在問題分析、現(xiàn)實應(yīng)用等方面有所欠缺。那么如何培養(yǎng)學(xué)生的抽象思維能力？我?guī)ьI(lǐng)學(xué)生開展過無數(shù)次的教學(xué)探究活動，現(xiàn)根據(jù)自己多年的教學(xué)實踐談?wù)勼w會。

一、加強操作，手腦結(jié)合，梳理思維過程

在教學(xué)過程中，教師不但要讓學(xué)生學(xué)會動腦，還要讓學(xué)生學(xué)會動手。通過動手，能夠讓學(xué)生在操作活動中展開探究，從而找到問題的答案。因此，教師要多組織一些操作活動，帶領(lǐng)學(xué)生從玩中學(xué)，在操作中學(xué)，借助動手操作，學(xué)生的各個感官協(xié)同參與，不但能夠梳理思維過程，而且能夠進一步提升抽象思維的能力[1]。

例如，在教學(xué)正方體和長方體的時候，對于小學(xué)生來說，幾何圖形中的立體空間過于抽象，不能建立一個具體清晰的直觀印象，這就為教學(xué)帶來一定的困難。尤其是正方體的展開圖這個內(nèi)容，學(xué)生在學(xué)習(xí)時，很難理解如何才能夠“沿著虛線折疊后圍成一個正方體”，學(xué)生也就不能用正方體的展開圖來判斷是否能夠圍成正方體。學(xué)生的困惑在于其對于正方體的展開圖，并沒有建構(gòu)清晰的直觀認(rèn)知。也就是說，在學(xué)生的頭腦當(dāng)中，沒有建立一個動態(tài)的形象，如果學(xué)生能夠在頭腦當(dāng)中建立直觀感知，那就有了立體空間的思維基礎(chǔ)。此時該如何突破學(xué)生的認(rèn)知困境呢？我特意引導(dǎo)學(xué)生展開了動手動腦的操作活動。

我將學(xué)生分成幾個小組，同桌兩人為一組進行合作。將一個正方體的紙盒剪開，并明確要求學(xué)生是沿著棱剪開。剪開之后就平放在桌面上。接著，我引導(dǎo)學(xué)生，將剪開的平面圖還原成一個正方體的紙盒。學(xué)生完成了這兩項操作之后，我讓學(xué)生進行觀察，并分組討論。討論的內(nèi)容是：看一看展開圖有什么不同，有什么相同。于是學(xué)生根據(jù)自己的操作，展開了討論。有的學(xué)生經(jīng)過討論后發(fā)現(xiàn)，展開圖的中間是4個，上下各是1個，但卻具有不同點，那就是單獨的兩個有所不同，一個是對稱的，另一個是錯開的。根據(jù)學(xué)生的這個反饋，我進行引導(dǎo)，我們可以把這種上面一個，中間四個的圖形叫作“141”型，并循著這個線索，繼續(xù)引導(dǎo)學(xué)生思考，像這樣的圖形還可以繼續(xù)分類，動手畫一畫，在自己的展開圖上標(biāo)出來。學(xué)生經(jīng)過操作，能夠?qū)⒉煌愋偷恼归_圖直觀形象地呈現(xiàn)出來，我引導(dǎo)學(xué)生將這些直觀圖進行有序呈現(xiàn)、有序整理，其實也是對思維有一個有層次的梳理，學(xué)生得到了如下整理好的呈現(xiàn)圖，如圖1～6。

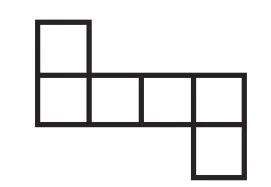
圖1

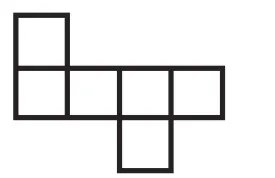
圖2

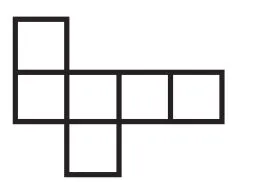
圖3

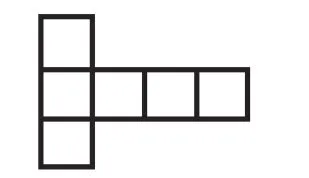
圖4

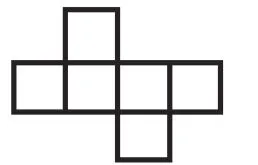
圖5

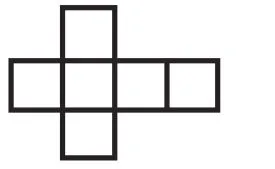
圖6

我繼續(xù)引導(dǎo)學(xué)生思考：想一想除了“141”型，還有其他的類型嗎？再操作試試看。學(xué)生繼續(xù)動手操作，發(fā)現(xiàn)還有一種類型，就是上面1個，中間3個，下邊2個。學(xué)生稱之為“132”型。學(xué)生自然而然地想要深入探究這種“132”型的展開圖，還有哪些不同的分類。根據(jù)之前的有序探究模式，學(xué)生很快就整理好呈現(xiàn)圖，如圖7～9。

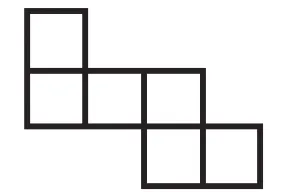
圖7

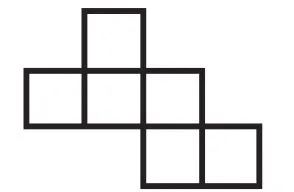
圖8

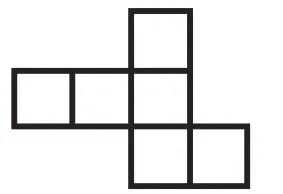
圖9

還有學(xué)生通過操作很快就發(fā)現(xiàn)了另外一種展開圖式，如圖10～11，前者是“222”型，后者是“33”型。

圖10

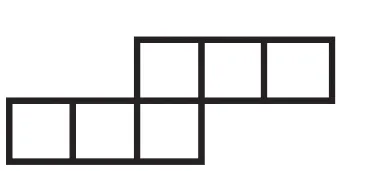
圖11

在學(xué)生操作之后，我引導(dǎo)學(xué)生進行總結(jié)：想一想，將正方體展開，共有幾種情形？這個展開的過程中，你有什么樣的發(fā)現(xiàn)？說一說自己的思路。學(xué)生發(fā)現(xiàn)，正方體展開之后，共有11種圖型，并且有一個規(guī)律，展開之后連成一排都不可能超過四個面。由此學(xué)生推論，如果一個圖形有四個正方形可以圍成一個“田”字，那么這個圖形就不可能圍成正方體。

以上教學(xué)環(huán)節(jié)，教師從直觀形象的思維入手，借助動手操作，加強感官協(xié)作，組織學(xué)生展開探究。學(xué)生通過動手操作，在積極思考中不斷梳理自己的思維過程，讓抽象思維由雜亂走向有序，得到完善和發(fā)展。

二、數(shù)形結(jié)合，拓展延伸，提升思維品質(zhì)

在小學(xué)數(shù)學(xué)教學(xué)中，數(shù)形結(jié)合是幾何直觀思維的有效體現(xiàn)。教師借助數(shù)形結(jié)合，能夠幫助學(xué)生直觀感知立體空間，由此，從具體到抽象展開延伸拓展，有效建構(gòu)抽象的立體思維，提升學(xué)生的思維品質(zhì)[2]。

圖12

例如，在學(xué)完正方體之后，我出示了這樣一道思考題：一塊正方體木塊六個面都涂上了顏色，現(xiàn)要將它切成64塊大小相等的小正方體，如圖12。

問：三面涂色、兩面涂色、一面涂色的小正方體塊分別有多少塊？學(xué)生經(jīng)過觀察之后認(rèn)為，正方體有8個頂點，所以三面涂色的就有8個；兩面涂色的跟棱長有關(guān)聯(lián)，所以兩面涂色的有24個，一面涂色的跟長方體的面有關(guān)，所以一面涂色的有24個。在學(xué)生的直觀觀察之下，這個問題已經(jīng)得到了解決。學(xué)生應(yīng)該說已經(jīng)掌握了正方體的特征。此時，我運用數(shù)形結(jié)合展開拓展延伸，對學(xué)生的抽象思維進行訓(xùn)練：

訓(xùn)練一：

如果要將這個正方體木塊的每個面都均勻切上四刀，一共可以切多少個小正方體？其中，三面涂色的有多少個？一面涂色的有多少？沒有涂色的有多少個？

學(xué)生在之前練習(xí)的基礎(chǔ)上，展開解答，認(rèn)為三面涂色跟頂點有關(guān)，無論怎么切，三面涂色都是8（個）；一面涂色（5-2）×（5-2）×6=54（個）；沒有涂色的就是一個正方體，（5-2）3=27（個）。

訓(xùn)練二：

如果將正方體的木塊，每個面均勻切n刀，一共可以切多少個小正方體？其中，三面涂色的有多少個？沒有涂色的有多少？

根據(jù)具體數(shù)據(jù)，學(xué)生對訓(xùn)練二也有了解答：切n刀，每條棱上就有n+1個小正方體，三面涂色8個；沒有涂色的其實形成了一個正方體，（n-1）3。

以上環(huán)節(jié)，教師借助數(shù)形結(jié)合，將抽象思維的要求難度加大，帶領(lǐng)學(xué)生拓展延伸，從而最終實現(xiàn)了抽象思維的發(fā)展和提升。

三、豐富經(jīng)驗，結(jié)合實際，內(nèi)化抽象思維

數(shù)學(xué)教學(xué)的本質(zhì)，是培養(yǎng)學(xué)生將抽象思維內(nèi)化為自己的技能，將數(shù)學(xué)思維應(yīng)用在生活實踐當(dāng)中。這就需要教師結(jié)合實際，給學(xué)生提供機會，帶領(lǐng)學(xué)生走出課堂，親身經(jīng)歷應(yīng)用數(shù)學(xué)分析問題、解決問題的實踐過程，從而豐富學(xué)生的經(jīng)驗，內(nèi)化學(xué)生的抽象思維。

例如，在教學(xué)計數(shù)單位“萬”這一內(nèi)容時，我結(jié)合學(xué)生的實際生活，要求學(xué)生預(yù)估圖書館藏書量，預(yù)估體育館座位數(shù)量，在這個日常現(xiàn)實生活當(dāng)中司空見慣的數(shù)學(xué)任務(wù)驅(qū)動下，學(xué)生不但豐富了經(jīng)驗，而且對“萬”這個計數(shù)單位有了更深刻的認(rèn)識。再如，在教學(xué)“公頃”這個概念后，我組織學(xué)生參觀植物園，參觀學(xué)校校園，參觀周圍的建筑，沿著大約一公頃面積的土地，四周走一圈。先從動態(tài)的角度，直觀感知一公頃的面積大小，然后，讓學(xué)生對菜農(nóng)進行訪問交流，了解一百平方米面積所種作物的產(chǎn)量和產(chǎn)值。通過這樣的實際引導(dǎo)，讓學(xué)生感悟到數(shù)學(xué)在現(xiàn)實生活當(dāng)中的應(yīng)用。

結(jié) 語

在數(shù)學(xué)課堂教學(xué)中，教師從學(xué)生的思維角度出發(fā)，組織操作探究活動，加強從直觀到抽象的過渡，引導(dǎo)學(xué)生手腦并用，能夠幫助學(xué)生提升抽象思維，使其更具有靈活性和邏輯性。

[1] 肖耕文.小學(xué)數(shù)學(xué)概念的教學(xué)策略與強化途徑[J].江蘇教育研究,2014,(23):59-61.

[2] 屠桂芳.過程與結(jié)果是數(shù)學(xué)活動的雙翼[J].江蘇教育研究,2016,(14):7-11,2.