4100 型內燃機曲柄連桿機構動力學仿真分析

李靜敏，趙蘭英，劉 松，任思航，婁永昌，曹其政，趙軍軍

（1.大連施奈萊克創新汽車零部件有限公司，遼寧，大連116600；2.大連海洋大學，遼寧 大連 116023）

0 引言

隨著內燃機技術的高速發展，使得內燃機在振動、噪聲以及運動平穩性等動力學問題方面變得更加突出，更加近距離的進入到人們的視線內。對內燃機的運動系統的動力學分析和慣性力的平衡、曲軸的振動分析與減振設計、機體的振動分析以及內燃機的減振與隔振等國內外學者已經作了大量的工作[1-3]。數字仿真技術已經開始廣泛應用于內燃機研究、設計和開發的諸多領域。張兆強等[4]運用多體動力學理論對內燃機進行整機模態分析和振動分析，結果說明整機模態分析比單純構件模態分析更能反應出內燃機的實際工況，為內燃機力學性能分析形成另一種重要方法，同時為內燃機的減振降噪問題提供一些理論依據。胡愛閩等[5]采用三維設計軟件Pro/E對曲軸系統進行結構設計，在機械仿真軟件ADAMS環境中搭建柴油機曲軸系統的虛擬樣機，分析氣缸活塞位移、速度及加速度的運動規律，以及氣缸側壓力和曲柄銷受力情況，同時對作用在曲軸上的扭矩進行分析。戎瑞亞等[6]運用Solidworks和仿真軟件ADAMS建立了船舶柴油機及其軸系的虛擬樣機模型，并進行運動學與動力學仿真，獲取了仿真模型的運動學和動力學特性數據。利用該動力學模型，改變柴油機的支承條件，對隔振情況下的振動特性進行分析。高爽等[7]利用ADAMS軟件建立曲柄連桿機構虛擬樣機模型，PRO/E與ANSYS軟件對曲軸進行柔性化處理，利用曲柄連桿機構的動力學仿真分析結果進行后續的發動機整機振動、噪聲分析、疲勞壽命分析和研究。本文首先選取4100型內燃機基本設計參數，然后對曲柄連桿機構建模分析，通過動力學仿真分析驗證內燃機設計理論計算的有效性，同時對該機型進一步的改進設計和優化提供依據。

1 4100型內燃機三維模型的建立

1.1 4100型內燃機基本參數

活塞、連桿主要尺寸如表1所示，曲軸、軸承主要尺寸如表2所示。

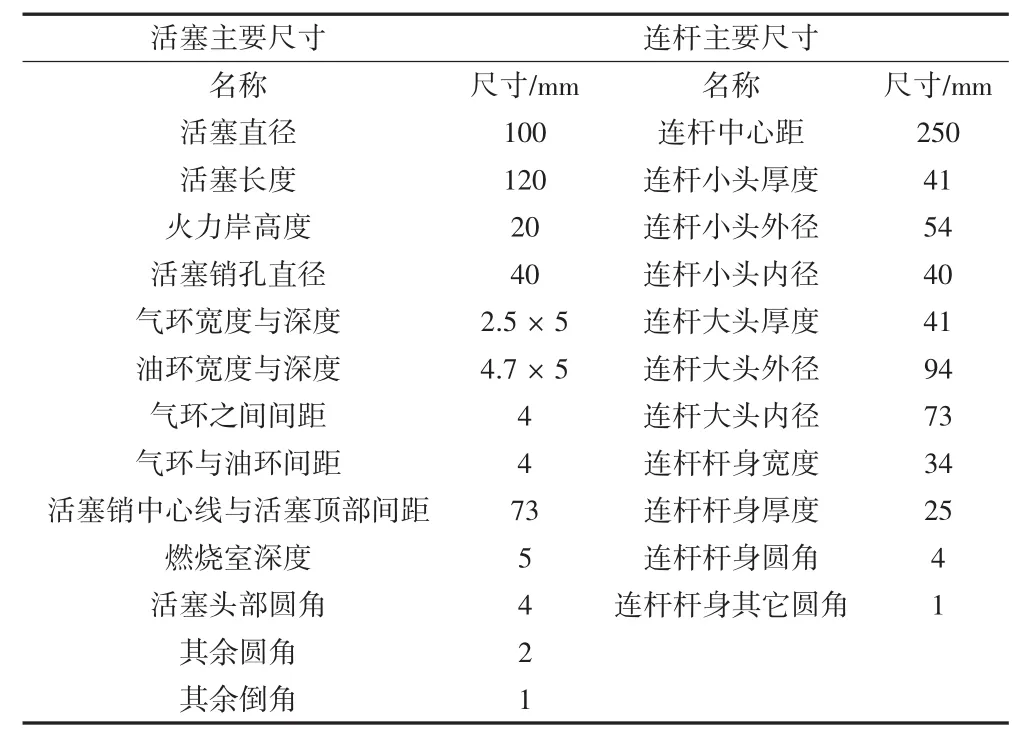
表1 活塞、連桿主要尺寸

表2 曲軸，軸承主要尺寸

1.2 三維建模

根據表1的曲柄連桿機構的主要尺寸，通過Solidworks軟件繪制內燃機活塞、活塞銷、連桿、曲軸飛輪組、軸瓦以及主軸承等的零件圖并進行裝配[8,9]，繪制4100型內燃機的曲柄連桿機構裝配圖如圖1所示。

圖1 4100型內燃機的曲柄連桿機構圖

2 動力學仿真

模型導入動力學仿真軟件建立動力學仿真模型如圖2所示，添加各個零件模型材料，依次添加各零件屬性，建立仿真模型。

圖2 動力學仿真模型

2.1 添加約束

在ADAMS/View軟件給內燃機曲柄連桿機構零件模型添加運動副（connectors）,它用來保證零件之間的連接狀態以及零件之間的相對運動情況，使模擬系統趨于真實的運動情況。

2.2 施加載荷

式（1）～（4）中 S 為氣缸工作容積，Sc為余隙容積，Sx為氣缸在某點的氣缸容積。因此施加在活塞面上的載荷為Pg×（D2×π/4），根據動力學計算用表，將轉角轉換為時間公式為2 200×360°/60 000=13.2 °/ms，時間 T=C/13.2.根據動力學計算用表，計算氣體力，通過傳統理論計算得出第一缸理論所受的活塞和與時間的數據。由著火順序1-3-4-2，遠離飛輪端為第1缸，依次2、3、4缸，其它缸依次相差180°.

根據活塞在缸內壓力數據計算而得活塞受力隨時間的變化關系繪制曲線，橫坐標X表示時間（ms），縱坐標Y表示活塞所受到的力（N）。根據4100內燃機的著火順序1-3-4-2，缸與缸之間相差180°.因此可以通過第一缸的活塞受力可以得出其它3缸的活塞所受力與時間的關系曲線。根據活塞所受的合力施加到每一缸活塞之上。根據理論計算的壓力來進行仿真計算。

2.3 驅動應用和模型測試

驅動是作為一種約束添加，而且是時間的函數，在模型上添加驅動是將運動副未約束的自由度進行約束。本次的施加驅動方法是利用所選仿真軟件工具欄中的Motions中的驅動按鈕，給曲柄連桿機構模型添加驅動。選擇Motion工具中的Rotational Join motion （應用旋轉副驅動），將轉速調整為 13.2°/ms，實際轉速計2 200 r/min.

3 仿真結果分析

3.1 活塞參數曲線及分析

仿真得出的第一缸活塞關于Y軸的各類曲線如圖3所示。

圖3 第一缸仿真變化各曲線

由圖3可知活塞的最大位移值是123.952 3 mm、活塞的最大速度值是14.843 4 mm/ms（即14.843 4 m/s）、活塞加速度在時間為13.443 3 ms和40.693 3 ms（即轉角為177.451 56°和537.151 56°）時達峰值2.487 8 mm/ms（2即2 487.8 m/s2），時間在27.61 ms（即轉角為364.452°）時達到峰值-4.145 6 mm/ms（2即-4 145.6 m/s2）、活塞往復慣性力在時間為13.443 3 ms和40.693 3 ms（即轉角為 177.4515 6°和 537.1515 6°）時達峰值6.219 5 mm/ms（2即6 219.5 N），時間在27.61 ms（即轉角為364.452°）時達到峰值-10.3633 mm/ms2（即-1036 3.3 N）、活塞總作用力達到最大值為46 888.007 N、活塞側推力達到最大值為3 190.275 3 N.

3.2 連桿參數曲線及分析

連桿變化曲線如圖4～圖6所示，由圖可知連桿的側推力達到最大值為3 190.275 3 N、連桿合力達到峰值為40 941.688 1 N、連桿擺角峰值大約在±14.47°，呈正弦曲線周期性變化。

圖4 連桿的側推力變化曲線

圖5 連桿所受合力的變化曲線

圖6 連桿擺角變化曲線

3.3 曲軸受力曲線及分析

曲軸作為曲柄連桿機構的關鍵組件，它的受力是最復雜也是最難計算的[10-13]，在本次研究中分析曲軸的幾個受力曲線，如圖7～圖9所示：

圖7 曲軸的側推力（切向力）變化曲線

圖8 單缸曲軸轉矩變化曲線

圖9 多缸輸出轉矩

由曲軸的側推力變化曲線可以看出，曲軸的切向力在時間為 28.703 3 ms（即 378.883 56°）時，達到最大值 18 839.159 1 N，在時間為 26.16 ms（即345.312°）時，達到最小值為-6 093.333 7 N.由單缸曲軸轉矩變化曲線可以看出，曲軸時間在28.703 3 ms（即378.883 56°）時達到最大值為1 177.4 N·m.

3.4 主軸承受力曲線及分析

主軸承所受力的變化曲線如圖10所示：

圖10 主軸承切向力的變化曲線

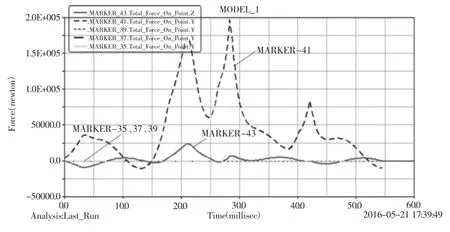
圖11 主軸承法向力的變化曲線

圖12 主軸承合力的變化曲線

通過主軸承切向力變化曲線可以看出，只有第四個主軸承和第五個主軸承受到切向力的影響，其他缸不受切向力的影響（即很小給予省略）。原因是：由于繪制的曲軸與飛輪同體，而且飛輪的質量相比于其它部件的相差較大，質心在第四、五軸承之間，因此在主軸承受力時出現，第一、二、三軸承受力非常小，第五個主軸承時間在21.073 3 ms（即278.167 56°）時達到最大值為24 202.178 4 N.第四個主軸承時間在21.436 7 ms（即282.964 44°）時達到最大值為1.491 ×108N.

由主軸承法向力變化曲線可以看出，第四個主軸承和第五個主軸承受到法向力的影響，其他缸不受切向力的影響（即很小給予省略）。第五缸曲軸時間在28.34 ms（即 374.088°）時達到最大值為 141 210 N.第四缸曲軸時間在28.34 ms（即374.088°）時達到最大值為-1.971 6×105N.

由主軸承法向力變化曲線可以看出，第四個主軸承和第五個主軸承受到法向力的影響，其他缸不受切向力的影響（即很小給予省略）。第五缸曲軸時間在28.34 ms（即 374.088°）時達到最大值為141 210 N.第四缸曲軸時間在28.34 ms（即374.088°）時達到最大值為1.436 7×105N.

3.5 傳統結果與仿真結果對比

通過4100型內燃機整機設計參數，在已知曲柄連桿機構的一些理論變化曲線的基礎上。對仿真結果與傳統理論計算結果進行對比分析如表所示（誤差允許范圍在5%內）見表3：

表3 理論結果與仿真結果對比

綜上對比發現，仿真得出的受力曲線和轉矩輸出曲線與圖解理論計算得出的受力曲線和轉矩輸出曲線都有一定的差異。這是因為理論計算中沒有考慮到各運動部件的所受重力以及高速運動下的往復慣性力與旋轉慣性力[14-15]，而ADAMS中所建立的虛擬樣機中進行仿真時，考慮到了部件的所受重力與高速運動下的慣性力，所以利用ADAMS建立曲柄連桿機構虛擬樣機模型來模擬4100內燃機曲柄連機構工作狀態，從而仿真計算機構的動力學特性結果更加精確且更加接近實際工作情況。

4 結論與建議

通過Solidworks建立曲柄連桿機構模型，進而在全剛性體和平衡狀態下進行動力學仿真分析，得出的結果不僅可以驗證設計的正確性，也可為內燃機的優化和改進提供依據，對提高設計質量和縮短開發周期具有很重要的實用價值。

（1）得出的受力曲線和轉矩輸出曲線與圖解理論計算得出的受力曲線和轉矩輸出曲線都有一定的差異，活塞的位移、速度、加速度的特性曲線與理論曲線相同，而由于活塞組質量理論與仿真相差較大，所以在有關慣性力的特性曲線上，仿真與理論的結果相差較大，經實測四缸機活塞質量，發現理論計算中活塞質量偏差較大，仿真活塞組質量更接近實測值。

（2）由于理論計算中沒有考慮到各運動部件的所受重力，而ADAMS中所建立的虛擬樣機中進行仿真時，考慮到了部件的所受重力的影響，所以有關慣性力的曲線結果存在較大差異。

（3）不僅僅是質量的問題，還有氣體力和著火順序與時間的關系也是由推導獲得的影響。因此，往往仿真數據結果與理論結果有偏差是不可避免的，只有不斷增強理論計算的精確性誤差才可不斷減小。

（4）利用ADAMS建立曲柄連桿機構虛擬樣機模型來模擬4100內燃機曲柄連機構工作狀態，由于虛擬樣機考慮因素比較全面，從而仿真計算機構的動力學特性結果更加精確且更加接近實際工作情況。