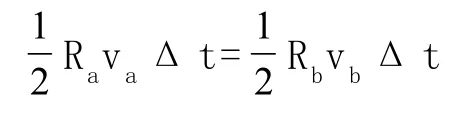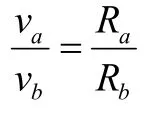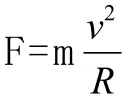巧用曲率半徑解決物理問題

張方彥

（南京市人民中學，江蘇南京 210018）

1 題目

如圖1為地球繞太陽運行的橢圓軌道，太陽位于橢圓的一個焦點上，a為近日點，b為遠日點，地球在a、b兩點的速度和與太陽的距離分別為V、V；R、R。求速度之比。

2 錯誤解法

根據萬有引力定律和牛頓運動定律建立關系：

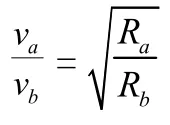
這是學生在解答過程中經常出現的錯誤。

3 分析

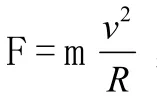
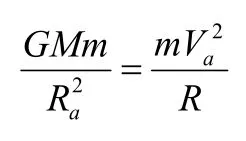
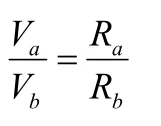
根據以前的教學的經驗，學生在這個地方經常會問，上面求曲率的方法有沒有理論依據？曲率半徑真的是相等的嗎？

正確解法：如圖3所示，太陽位于橢圓的焦點s處，太陽的質量為 M,地球的質量為m。在頂點1、2之間機械能守恒及開普勒第二定律得；

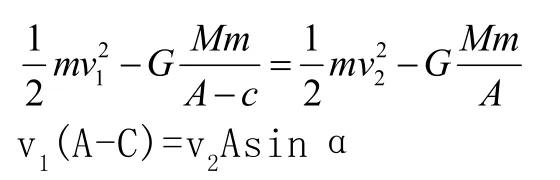
其中，c為橢圓的半焦距，即

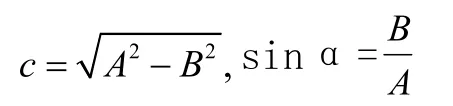
由以上方程可求得

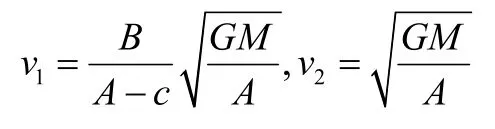
頂點1處的曲率半徑ρ可有地球在該處所受的萬有引力等于地球在該處的向心力求的，即

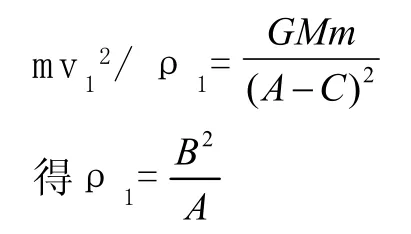
頂點2處的曲率半徑ρ可由曲率圓的向心力公式求得，即

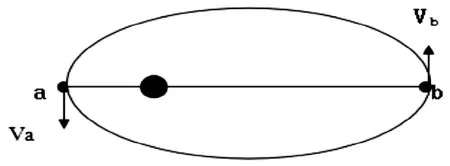
圖1 地球繞太陽運行的橢圓軌道

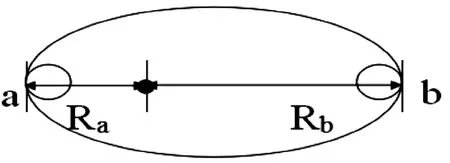
圖2 在近日點和遠日點作兩個跟軌道相切的圓

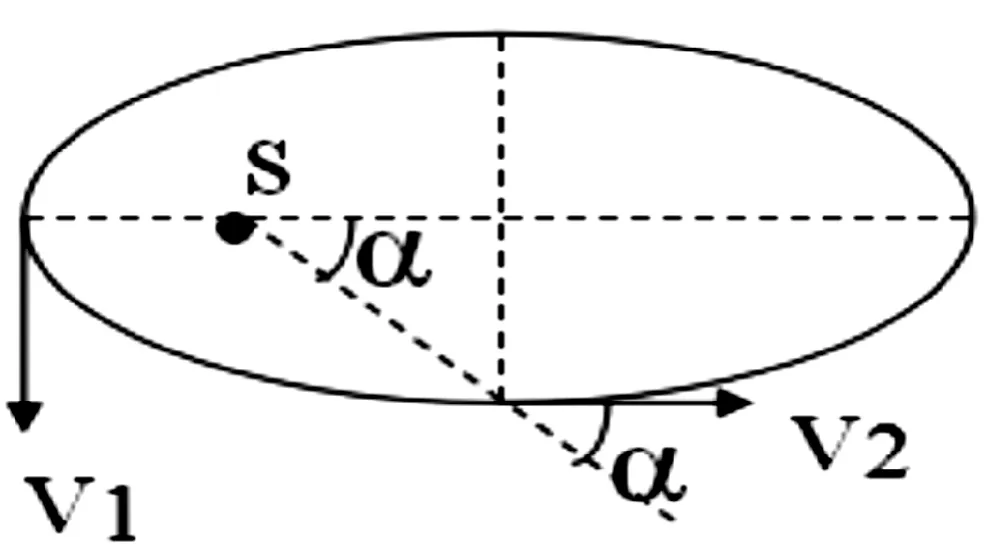
圖3 太陽位于橢圓的焦點

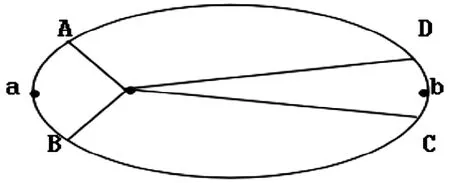
圖4 兩個扇形的面積圖

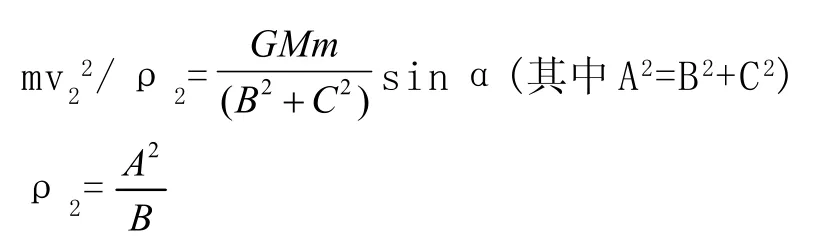
由上面的推導可以知道地球在近日點和遠日點的曲率半徑一定相等。

其實這個問題也可用開普勒定律來研究。根據行星運動的第三定律，行星沿橢圓軌道時，它和中心天體的連線在相等時間內掃過的面積相等，以近日點和遠日點為中心，取一個極短的時間間隔Δt，在這個時間內掃過的面積如圖4所示的兩個扇形的面積相等。

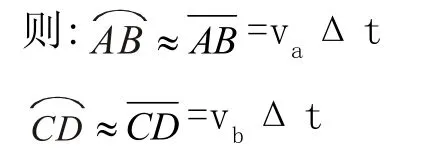
這兩個扇形的面積分別為：

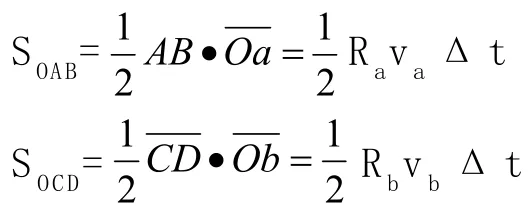
由于S=S可以得到