閱讀，不容忽視的數學學習技能

茅雅琳

[摘? 要] 數學教材、數學課堂、數學問題都具有其可讀性，都值得提倡和推廣. 閱讀課題，讓目標更明確;閱讀條件，讓已知更清晰;閱讀板書，讓結構更完善. 作為數學教師，我們要善于引導學生學會閱讀，學會思考.

[關鍵詞] 數學閱讀;學會對話

閱讀，是人類汲取知識的重要手段和認識世界的重要途徑，全民閱讀，終身閱讀的思想已經開始深入人心. 但是，很多時候閱讀被人為地與文科學習畫上了等號，在日常生活及教育教學中，每次提到閱讀，總是意味著閱讀文學作品. 其實，這是一個很大的誤區，數學學習同樣離不開閱讀，課程標準（2011版）明確提出“教材應具備可讀性，易于學生接受，激發學生學習興趣，為學生提供思考的空間”. 數學教材、數學課堂、數學問題都具有其可讀性，都值得提倡和推廣. 下面結合教學實際，列舉三點容易被師生忽視，卻至關重要的閱讀內容，以期和同仁研討商榷.

閱讀課題，讓目標更明確

教學片段1

教師：閱讀“中位數”這個課題，你認為中位數應該是怎樣的數呢？

學生1：處于中間位置的數.

教師：隨意給的一些數據，哪個數是中間位置的數呢？

學生2：我覺得應該排序，這樣研究中間位置的數才有價值.

教師：你這樣的建議非常合理，如果有奇數個數，用你的方法就可以確定中間位置的數，但是，如果有偶數個數據，怎樣確定中間位置的數呢？

學生3：那就取中間兩個數的平均數.

教學片段2

教師：閱讀“位似圖形”這個課題，請同學們分析，位似圖形應該具有什么特征？

學生4：我看到名稱里有個“似”，它們應該是相似圖形.

學生5：我看到名稱里有個“位”，它們應該是有特殊的位置關系.

學生6：相似我們已經研究過，今天研究位似，那一定是兩個相似圖形有特殊的位置關系，我很想知道，有怎樣特殊位置關系的相似圖形稱為位似圖形？

教學片段3

教師：閱讀“反比例函數”這個課題，猜想今天我們將學習什么內容？

學生7：學習一種新的變化過程，其中含有兩個變量.

學生8：就是學習一種新的函數.

學生9：這兩個變量之間的關系成反比例，小學學過反比例關系.

學生10：行程問題中，速度和時間就成反比例關系.

學生11：得說路程一定時，速度和時間成反比例關系.

學生12：也就是兩個變量的乘積為定值.

學生13：其中一個變量是關于另一個變量的反比例函數.

學生14：與前面學習的正比例函數的研究類似.

以上三個教學片段，孩子們通過閱讀課題，提煉本課研究的重點所在. 隨著教師問題的層層深入，學生從字面的意義，到概念的合理性，順利尋找到了中位數確定的方法，大致了解了位似的特征，發現了用類比方法學習反比例函數的基本思路. 其實，數學每個章節或者每一課時的課題，都值得引導學生很好地進行閱讀和分析，課堂上教師要給學生預留認真閱讀的時間，再通過生生、師生之間的交流探討，把腦海中因閱讀課題而引發的思考顯性地表述出來. 從課堂上師生的對話中可以看出，學生有能力對課題進行細致的剖析，能夠發現課題所蘊含的數學知識和學習方法.

閱讀條件，讓已知更清晰

眾所周知，數學學習離不開數學問題的解決，很多時候學生之所以不會解題，是因為他們不會讀題. “讀完條件，答案自現”并不是沒有可能，在認真閱讀題目條件后，已知信息會更通透，答案也呼之欲出.

本題改編自一道中考壓軸題，很多學生看到這樣的大題就產生畏懼心理，根本不敢嘗試. 其實由以上的分析可知，隨著閱讀的層層推進，題目中的已知條件逐漸清晰. 閱讀分析的過程，就是把壓軸題分解成幾個小問題的過程，教學實踐顯示，在這樣的閱讀指導下，班級有90%的學生能夠求得第一種情況，50%的學生能夠求得完整的答案.

閱讀板書，讓結構更完善

隨著多媒體的介入，現在的很多課堂不再注重板書，有些課堂甚至已經發展到沒有板書. 其實，無論教學課件設計得多么精美，總是存在碎片化、快速化的弊端. 板書在教學過程必不可少，教學的重要內容，解題的關鍵步驟等都有必要在黑板上系統呈現，需要在學生的視野和腦海中做必要的停頓.

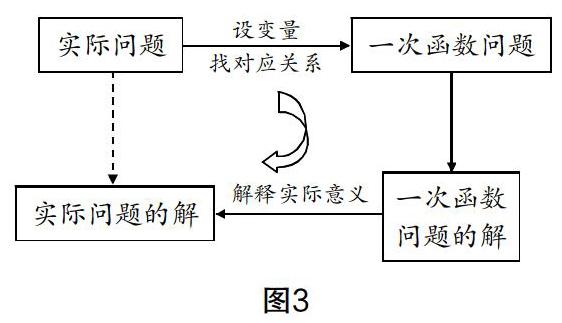
建構主義認為，知識并不能由教師或其他人傳授給學生，只能由每個學生依據已有的知識和經驗主動地加以建構. 這個建構的過程，需要閱讀必要的板書作為媒介. 課程標準也指出“必要的板書有利于實現學生的思維與教學過程同步，有助于學生更好地把握教學內容的脈絡”. 例如，我們在進行“19.2一次函數”教學中，可以設計如下板書：

通過閱讀這個板書，學生對用函數解決實際問題有了系統的認識. 遇到實際問題，可以通過設變量，找對應關系，將實際問題轉化為一次函數問題，再利用一次函數的解，來解釋實際意義，進而得出實際問題的解. 這有利于學生后續在面臨實際問題時，產生建立函數模型的意識，進而找到解決問題的途徑和方法，而這種模型思想同樣適用于解決其他實際問題.

閱讀課題，就是與文本對話，閱讀條件，就是與題目對話，閱讀板書，就是與自己對話. 作為數學教師，我們要善于引導學生學會閱讀，學會思考.