多樣化教學形式培養小學生的數感

安徽省滁州市解放小學 王德菊

新課程標準（2011年版）這樣表述：數感主要是指關于數與數量、數量關系、運算結果估計等方面的感悟。建立數感有助于學生理解現實生活中數的意義，理解或表述具體情境中的數量關系。數感在新課程標準十個核心概念中處于首要位置，可見它的重要性。了解了數感的內涵和它的重要性，我在教學活動中把理論和實際充分結合，設計出許多不同的情境，采用各種方式來培養學生的數感。

一、利用學生已有的生活情境培養學生的數感

我在上《因數和倍數》新課導入時，用了一張祖孫三代溫馨甜蜜的照片，要求學生根據自己的生活經驗，說出每兩人之間的關系，同學們很快就指出圖中兩兩之間的關系。從生活中人與人之間的關系引導出本節課要學習的因數與倍數的關系，讓學生充分明確哪個數是哪個數的因數，哪個數是哪個數的倍數，而不能弄成哪個數是因數，哪個數是倍數，因數和倍數是相互依存的，不能單獨存在。這樣在不知不覺中學生就掌握了因數和倍數的關系。把所學的新知識與學生已有的生活情境有機結合，就非常容易使學生掌握住新的知識。

二、通過激趣導入培養學生的數感

在教學《圓的周長》時，我創設了龜兔賽跑的情境。龜兔賽跑的故事同學們都很熟悉，大家都知道結果是兔子輸了。兔子的驕傲導致輸了那場比賽。后來兔子越想越不服氣，于是邀請烏龜進行第二次比賽。兔子為了確保勝利，畫了兩條比賽路線（如下圖）：

圖1 龜兔賽跑

兔子跑里面的圓形路線，烏龜跑外面的正方形路線，結果兔子贏了這場比賽，觀眾紛紛表示比賽不公平。同學們知道為什么不公平嗎？學生一下子被這有趣的龜兔賽跑的故事情節吸引，對數學學習產生了好奇心和求知欲，從而引發新的數學問題，啟發他們主動參與探索新知的熱情，為新課的學習創設了良好的學習氛圍。

三、運用轉化的思想培養學生的數感

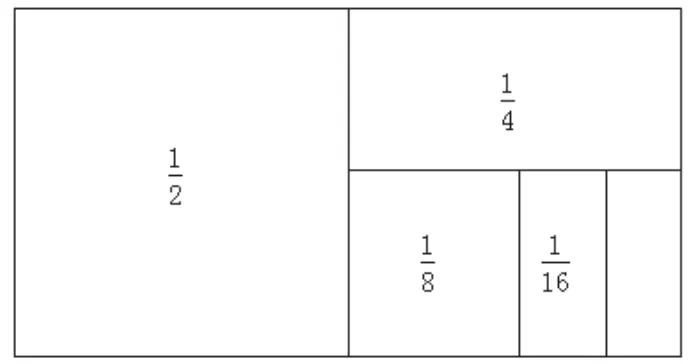
這道題運用了數形結合的思想，既加深了學生對轉化策略的理解，又讓學生產生了思維碰撞。借助數形結合的思想進行算式的轉化，把一道加法算式轉變成一道非常簡單的減法算式：

在運用轉化策略解決實際問題時，我們要引導學生靈活變換思考問題的角度，尋找簡捷的解題方法，逐步積累運用轉化策略解決問題的經驗，增強學生解決問題的策略意識，從而達到培養他們對數的感知認識。

四、拓展課外知識培養學生的數感

《3的倍數的特征》一課中的例5是在1～100中圈出3的倍數，尋找3的倍數的特征，然后在計數器上分別表示出幾個3的倍數，看看各用了多少個珠子，最后總結出3的倍數的特征，即各個位的數字之和是3的倍數，這個數一定是3的倍數。

在探索3的倍數的特征過程中，這些數都是比較小的數，如果出現位數多，數比較大，有沒有更好的方法呢？我因勢利導，給學生介紹一種“篩法”的方法,這是課外知識的延伸。這種方法是把各個數位的數字先篩去3的倍數或和為3的倍數的數，若余下的數字之和是3的倍數，原數就是3的倍數，否則就不是3的倍數。

通過書本和課外知識的結合，學生在操作、觀察、比較、驗證、歸納等活動中，獲得了對知識的正確結論，讓學生體會到了探究數學的樂趣。

五、利用故事中蘊含著的數學思想培養學生的數感

其實在許多耳熟能詳的故事中，都蘊含著十分深邃的數學思想。數學思想是數學的靈魂，學生如果理解掌握了它，就一定能從中體會到數學的奧妙。若能將故事中蘊含著的數學思想很好地運用到學習中，一定能加深學生對知識的理解，并能使他們獲得數學的靈感、啟迪思維，讓數學素養與文化素養達到雙重提高。

“司馬光砸缸”的故事應該是無人不曉，當其他小朋友對掉入水缸的小朋友都束手無策而驚慌失措時，聰明機智的司馬光在緊急關頭砸破水缸，成功地救出了那個落水的小朋友。一般人首先想到的是“讓人離開水”，但是水缸太高就沒有辦法了，而司馬光想到的是“讓水離開人”。這個故事把一個深奧的道理變得淺顯易懂，這就是逆向思維帶來的奇效。數學教學活動中，經常運用逆向思維的方式來加深對概念的理解或公式的鞏固應用，解決學習中的實際問題。

在教學5的倍數的特征時，可以說5的倍數的個位上是5或0，反過來，個位上是5或0的數，一定是5的倍數；乘法分配律的字母公式：（a+b）×c=a×c+a×c，反過來，a×c+a×c=（a+b）×c。

逆向思維能充分發揮學生的思考能力，有利于培養他們思維的廣闊性，激發學生的主觀能動性和探索新知識奧秘的興趣性。在小學數學教學中，學會了逆向思維法，不僅能增加一種解題方法，而且對培養學生的推理能力也有著積極意義。如果學生掌握了這種思維方式，那么他們考慮問題時的思路就會更開闊，思想就會更活躍。

培養學生擁有良好的數感，不是一朝一夕就能獲得的，它需要一個循序漸進的過程。在教學中，我充分利用學生已有的生活經驗，采用多樣化的教學形式，把學生所學的數學知識應用到生活中去，解決身邊的實際問題，讓學生體會到學習數學的重要性，強化他們的數感，并對所學的知識做到融會貫通，讓數感伴隨著學生一起成長。

[1]孔慧英，梅智超．現代數學思想概論[M]．北京：中國科學技術出版社，1993 ．