用方程思想解決實際問題

福建省南安市康美中學 戴燦陽

一、用方程方法解決幾何問題

例1如圖所示，用一塊長方形鐵片，在它的四角上各自剪去一個邊長是4cm的小正方形，然后把四邊折起來，恰好做成一個沒蓋的盒子。已知鐵片的長是寬的2倍，做成的盒子容積是1536cm3，求這塊鐵片的長和寬。

解析：本題是求長方形的長和寬，已知是把該圖形折成長方體并已知容積，長方體的容積公式即為本題的等量關系式。

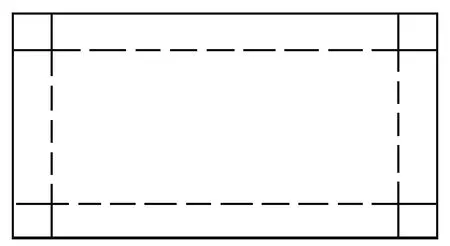
由已知，假設寬為xcm，則長為2xcm，長方體盒子的底面是一個長方形，長是（x-8）cm，寬為（2x-8）cm它的底面積為（x-8）（2x-8）cm2。長方體的容積為1536 cm3，所以就可以列出方程：（2x-8）（x-8）×4=1536。

解此方程，求得方程的根并檢驗，確定方程的根，從而求得這塊鐵片的長和寬。

本題考查幾何體的容積，通過假設適當的未知數，再利用長方體的容積公式就得到了一元二次方程，利用一元二次方程的解法求出它的解，檢驗答案的合理性，就解決了這個問題。

例2求直線y=-x+2與直線y=3x-1的交點坐標。

分析：這種求函數圖象交點坐標的問題是與函數有關問題中的一類常見問題，要直接利用函數圖象準確地找出交點坐標，對于尺規作圖的方法很難做到，把求直線與直線的交點坐標看作求方程組的解就可以解決了。

∴這兩直線的交點坐標為（2，-1）。

兩條直線的交點實際上就是它們的公共點，這和方程組的思路是相通的，即兩個方程的公共解，所以采用方程組的方法。

二、用方程思想解決經濟問題

如華東師大（2008）版九年級（上）有一題：

例3陽江市政府考慮在兩年后實現市財政凈收入翻一番，那么這兩年中財政收入的平均年增長率應為多少？

解析：本題要理解翻一番的意義。可以假設原來的財政凈收入為a，兩年以后財政凈收入就是2a，再假設平均年增長率為x，相等關系就是財政凈收入翻一番。可列方程：

A（1+x）2=2a。

解得方程的兩個解，檢驗把不符合題意的解舍去，確定方程的解，從而求出這兩年的年平均增長率。

本道問題沒有一個數據，需要大膽假設，用什么不同的思路去思考問題，最后找到方程的方法，要有不怕失敗的精神，才能使問題得以解決。

例4某商場將每件進價為80元的某種商品按每件100元出售，一天可售出100件，后來經過市場調查，發現這種商品單價每降低1元，其銷售量可增加10年。

（1）求商場經營該商品原來一天可獲利多少元？

（2）若商場經營該商品一天要獲利2160元，則每件商品應降價多少元？

解析：關于利潤問題，有公式：總利潤＝每件商品的利潤×銷售數量，每件商品的利潤=銷售單價-進價。本題的關鍵是銷售量和銷售單價緊密相關，是一個函數關系，也是本題的難點，應采用逐步解決、化繁為簡的方法解決。（1）求出原來一天可獲利潤是一個代數問題，即：100×（100-80）＝2000（元）。而第（2）題應綜合運用兩個公式，利用（1）的方法及銷售量和銷售單價之間的關系，若假設每件應降價x元，則依據題意“每降低1元，其銷售量可增加10件”得：銷售量為(100+10x)件，類似（1）就可列方程：（100+10x）（100-80-x）＝2160。本方程是一元二次方程，求出它的解并檢驗，就可以得到問題（2）的答案了。

通過以上的例子我們可以看出，不論在代數或是幾何等數學分支，我們都可以利用方程的方法解決實際問題，可見方程對于解決問題的重要性。法國著名數學家笛卡兒曾說過：“自然界的一切問題都可以轉化為數學問題，一切數學問題都可以轉化為代數問題，而所有的代數問題都可以歸納為方程問題求解。”這句話似乎說得太絕對了，但無形之中又告訴我們：方程在數學中有著極其重要的地位，對解決問題發揮著巨大作用，它是解決問題的有力工具，它是一把頂省力的“杠桿”。 總而言之，方程對我們日常生活起著非常重要的作用，利用方程這個杠桿解決實際問題，就可以起到事半功倍的功效。

[1]魯曉琴．談方程模型思想的滲透[J]．文化教育，2007（2）：36．

[2]張楚廷．數學文化[M]．北京：高等教育出版社，2002．