一元不等式的圖像解法及其應用

☉安徽省宿州市第二中學 柏長勝

中學階段常見的一元不等式有整式不等式（一次、二次、高次不等式）、分式不等式、指數不等式、對數不等式、三角不等式、抽象不等式、含絕對值的不等式，以及它們之間的組合（或復合）不等式.因為這些不等式都只含一個未知數，故可統一地將這些不等式記為f（x）＞0（或f（x）＜0）.從數的角度看，這些不等式的解法各具特色，多姿多彩；若從函數圖像角度分析，它們則是統一的：函數y=f（x）的圖像在x軸上方的部分對應的是f（x）＞0，在x軸下方的部分對應的是f（x）＜0.因此，從函數圖像的角度可以找到這些一元不等式的統一解法.

一、整式不等式的圖像解法

例1 解下列不等式.

（1）x2-2x-3＞0；（2）x（x+2）（x-3）≥0.

解析：（1）方法1：方程x2-2x-3=0的根為x=-1或x=3，作出函數y=x2-2x-3的圖像，如圖1所示.

當x＜-1或x＞3時，函數y=x2-2x-3的圖像在x軸的上方，對應的函數值大于0，故不等式x2-2x-3＞0的解集為｛x|x＜-1或x＞3｝.

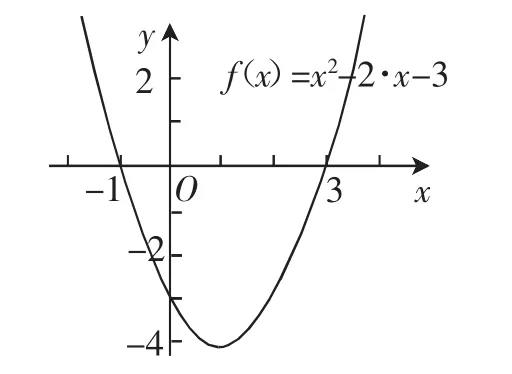
圖1

圖像法解整式不等式的一般流程為：（1）求根，（2）作圖，（3）寫解集.

因為我們只關注函數圖像在x軸上方的函數值為正的不變性（或圖像在x軸下方的函數值為負的不變性）及圖像與x軸的交點的不變性，而不必關注函數圖像的其他性質，因此，只需作出這些函數的拓撲圖像（必要時可以省略y軸）即可，如圖2所示.觀察函數圖像還可以發現，連續函數y=f（x）在由其零點分割的定義域內的每一個區域內的函數值符號都是相同的，因此，可以借助特殊點驗證法來確定原不等式的解集.

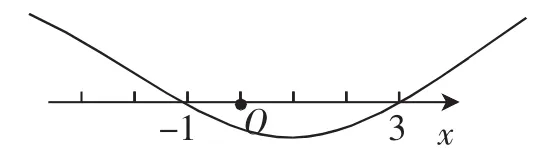
圖2

方法2：函數f（x）=x2-2x-3的零點為-1和3，其定義域被分成（-∞，-1），［-1，3］和（3，+∞）三個區域.

因為f（-2）=5＞0，f（0）=-3＜0，f（4）=5＞0，故不等式x2-2x-3＞0的解集為｛x|x＜-1或x＞3｝.

這種解法的一般流程為：（1）求零點，（2）分區間，（3）取值定域，簡記為“零點定界，特殊點定域”.用這兩種方法可以求出高次整式不等式的解集.

（2）方法1：方程x（x+2）（x-3）=0的根為-2，0，3，作出函數f（x）=x（x+2）（x-3）的拓撲圖像，因為x→+∞時，函數f（x）→+∞（或當x＞3時，f（x）＞0），因此，最高項系數為正的高次函數的圖像總是從x軸右上方開始（若最高項系數為負，可以先通過不等式同解變形變為正），如圖3所示.

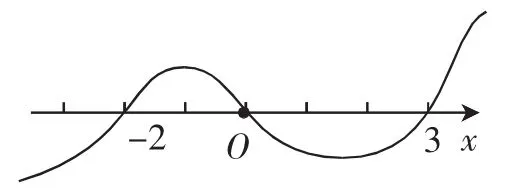
圖3

故原不等式的解集為｛x|-2≤x≤0或x≥3｝.

方法2：函數f（x）=x（x+2）（x-3）的零點為-1，0和3，其定義域被分成（-∞，-2），［-2，0］，（0，3）和［3，+∞）四個區域.

因為f（-3）＜0，f（-1）=4＞0，f（1）=-6＜0，f（4）＞0，故原不等式的解集為｛x|-2≤x≤0或x≥3｝.

二、分式不等式的圖像解法

三、指數與對數不等式的圖像解法

指數不等式af（x）＞ag（x）（a＞0，a≠1）可以等價變形為相應的整式不等式f（x）＞g（x）（a＞1）或f（x）＜g（x）（0＜a＜1），再運用整式不等式的圖像解法即可求出原不等式的解集.對數不等式在轉化為相應的整式不等式時要注意真數大于0.

四、三角不等式的圖像解法

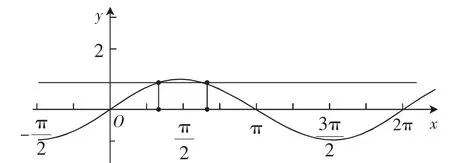
圖4

圖像法解形如sinx≥a（-1≤a≤1）的不等式的一般流程為：（1）作圖（y=sinx與y=a），（2）求交點（一個周期內），（3）寫解集（加上周期整數倍）.

五、抽象不等式的圖像解法

由抽象函數對應的不等式稱為抽象不等式，因為抽象函數無具體的解析式，圖像法是解決這類不等式的最佳方法.

例3已知函數f（x）為R上的奇函數，對于任意的兩個不相等的正數x1，x2，都有且f（3）=0，則不等式xf（x）＜0的解集為________.

解析：由題意知函數f（x）在（0，+∞）上單調遞增，又f（x）為R上的奇函數，故f（x）在（-∞，0）上單調遞增，且f（0）=0，f（-3）=-f（3）=0，可作出函數f（x）的拓撲圖像，如圖5所示.

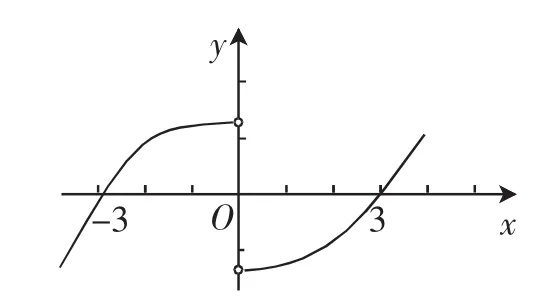
圖5

故不等式xf（x）＜0的解集為｛x|-3＜x＜0或0＜x＜3｝.

圖像法解抽象函數不等式的一般流程為：（1）分析性質（單調性、奇偶性、對稱性、周期性等），（2）求零點，（3）作圖像，（4）寫解集.

六、復合不等式的圖像解法

由復合函數對應的不等式稱為復合不等式，因為換元法是解決復合函數的根本方法，故換元法配合圖像法是解決這類不等式的最佳方法.

解析：令t=（fa），則（ft）≤2，作函數y=（ft）與y=2的圖像，如圖6所示.它們的交點橫坐標為-2，故不等式（ft）≤2的解集為｛t|t≥-2｝，再求出y=（fa）與y=-2的交點橫坐標為，故不等式（fa）≥-2的解集為｛a|a≤｝，所以不等式（f（fa））≤2的解集為｛a|a≤｝.

圖6

由本例分析可知，圖像法解形如f（f（x））＞a的復合不等式的一般流程為：（1）作函數y=f（x）的圖像，（2）令f（x）=t，（3）求出外不等式f（t）＞a的解集A，（4）再解內不等式f（x）∈A.

七、含絕對值不等式的圖像解法

例5 （2017年全國Ⅰ卷理23）［選修4-5：不等式選講］已知函數f（x）=-x2+ax+4，g（x）=|x+1|+|x-1|.

（1）當a=1時，求不等式f（x）≥g（x）的解集；

（2）若不等式f（x）≥g（x）的解集包含［-1，1］，求a的取值范圍.

解析：（1）當a=1時，分別作出函數f（x）=-x2+x+4和g（x）=|x+1|+|x-1|=的圖像，如圖7所示.

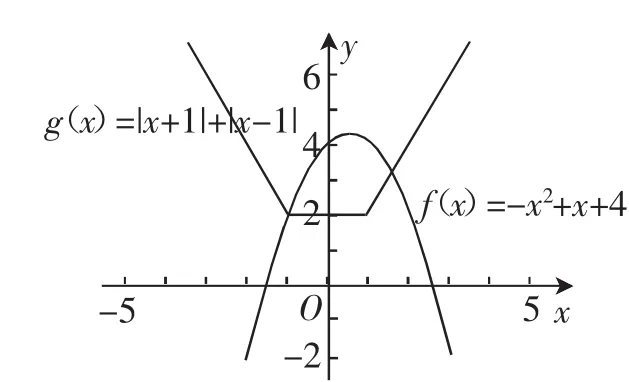
圖7

（2）當x∈［-1，1］時，g（x）=2.

所以f（x）≥g（x）的解集包含［-1，1］，等價于當x∈［-1，1］時f（x）≥2，即當x∈［-1，1］時-x2+ax+2≥0.作函數F（x）=-x2+ax+2的圖像，如圖8所示，所 以得-1≤a≤1.

圖8

所以a的取值范圍為［-1，1］.

圖像法解含絕對值不等式的一般流程為：（1）作圖（分段函數），（2）求交點，（3）寫解集.

八、圖像法解不等式的綜合應用舉例

例6（2017年全國Ⅰ卷理21）已知函數f（x）=ae2x+（a-2）ex-x.

（1）討論f（x）的單調性；

（2）若f（x）有兩個零點，求a的取值范圍.

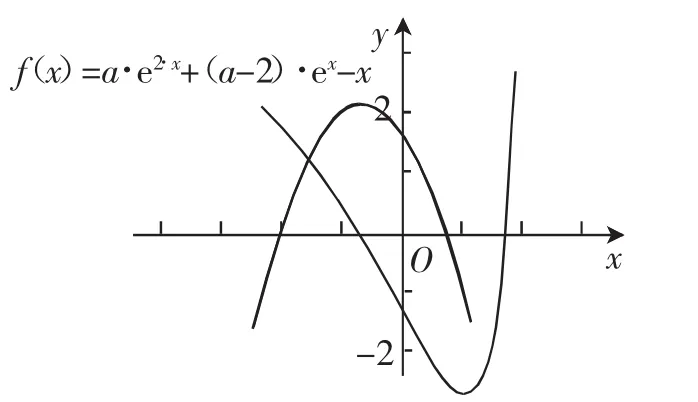
圖9

解析：（1）略.令F（t）=1-t-ln（tt＞0），因為F′（t）=-1-＜0，所以F（t）在（0，+∞）上單調遞減.又F（1）=0，x→0時，函數F（t）→+∞，作出函數F（t）的圖像，如圖10所示.

由圖10可知，不等式1-t-lnt＜0的解集為（1，+∞），所以，即0＜a＜1.

綜上，a的取值范圍為（0，1）.

另解1：不等式1-t-lnt＜0等價于1-t＜lnt，作函數y=1-t和y=lnt的圖像，如圖11所示.它們交點的橫坐標為1，由圖10可知，不等式1-t-lnt＜0的解集為（1，+∞），所以＞1，即0＜a＜1.

綜上，a的取值范圍為（0，1）.

另解2：令F（t）=1-t-lnt，因為F（t）只有一個零點1，且F（e）=1-e-1＜0，，所以不等式1-t-lnt＜0的解集為（1，+∞）.

綜上，a的取值范圍為（0，1）.

中學階段的一元不等式從結構形式來看只要掌握兩種類型的解法即可，形如f（x）＞0的不等式，其圖像解法的流程為：（1）求零點，（2）作圖，（3）寫解集；形如f（x）＞g（x）的不等式，其圖像解法的流程為：（1）作出兩個函數的圖像，（2）求交點，（3）寫解集.其他類型的不等式都可以等價轉化為這兩種類型的不等式進行求解.

1.王錫林.一元不等式的統一解法［J］.中學數學研究，2001（4）.

2.鄭明改.“不等式”統一的解法［J］.福建中學數學，2007（2）.

3.金迅嬰，李書超，王啟學.關于不等式的統一解法及其應用［J］.高等函授學報（自然科學版），2003（5）.F

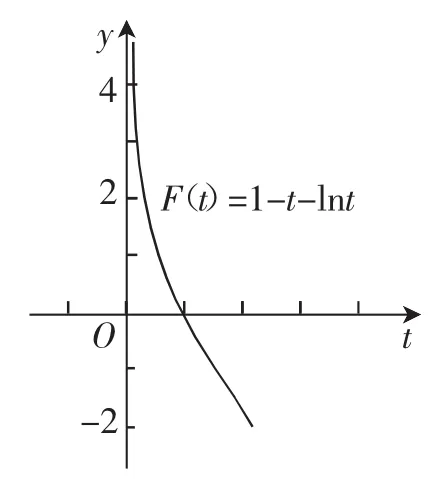
圖10

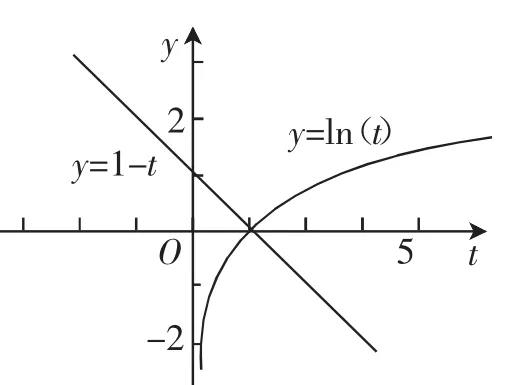
圖11